Với Giải SBT Toán 10 Tập 2 trong Bài 2: Biểu thức toạ độ của các phép toán vecto Sách bài tập Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.
Nội dung bài viết
SBT Toán 10 Cánh diều Bài 2: Biểu thức toạ độ của các phép toán vecto
Bài 12 trang 66 SBT Toán 10: Cho hai vectơ →u=(-1;3) và →v=(2;-5). Tọa độ của vectơ →u+→v là:
A. (1; - 2);
B. (- 2; 1);
C. (- 3; 8);
D. (3; - 8).
Lời giải:
Ta có: →u+→v= ( -1 + 2; 3 + (-5)) = (1; -2).
Vậy chọn đáp án A.
Bài 13 trang 66 SBT Toán 10: Cho hai vectơ →u=(2;-3) và →v=(1;4). Tọa độ của vectơ →u−2→v là:
A. (0; 11);
B. (0; - 11);
C. (- 11; 0);
D. (- 3; 10).
Lời giải:
Tọa độ của vectơ →u−2→v= (2-2.1;-3-2.4) = (0;-11)
Vậy chọn đáp án B.
A. (2; 4);
B. (- 3; 3);
C. (3; - 3);
D. (1; 2).
Lời giải:
Tọa độ trung điểm M của đoạn thẳng AB là:
xM= xA+xB2=4+(−2)2=1
yM= yA+yB2=−1+52=2
Suy ra M(1; 2)
Vậy chọn đáp án D.
A. (4;103) ;
B. (8; 4);
C. (2; 4);
D. (4; 2).
Lời giải:
Tọa độ trọng tâm G của tam giác ABC là:
xG=xA+xB+xC3=4+1+73=4
yG=yA+yB+yC3=6+2+(−2)3=2
Suy ra G(4; 2)
Vậy chọn đáp án D.
Bài 16 trang 66 SBT Toán 10: Cho hai điểm M(- 2; 4) và N(1; 2). Khoảng cách giữa hai điểm M và N là:
A. √13 ;
B. √5 ;
C. 13;
D. √37 .
Lời giải:
Khoảng cách giữa hai điểm M và N chính bằng độ dài vectơ →MN và bằng
|→MN| = √(xN−xM)2+(yN−yM)2=√(1+2)2+(2−4)2=√13
Vậy chọn đáp án A.
Bài 17 trang 66 SBT Toán 10: Cho hai vectơ →u=(-4;-3) và →v=(-1;-7). Góc giữa hai vectơ →u và →v là:
A. 900;
B. 600;
C. 450;
D. 300.
Lời giải:
Ta có: cos(→u;→v)
=
Suy ra (→u;→v)= 45o .
Vậy chọn đáp án C.
Bài 18 trang 67 SBT Toán 10: Côsin của góc giữa hai vectơ →u=(1;1) và →v=(-2;1) là:
A. −110 ;
B. √1010 ;
C. −√1010 ;
D. 310 .
Lời giải:
Côsin của góc giữa hai vectơ →u=(1;1) và →v=(-2;1) là:
cos(→u;→v)=
Vậy chọn đáp án C.
A. Tam giác đều;
B. Tam giác vuông tại A;
C. Tam giác có góc tù tại A;
D. Tam giác cân tại A.
Lời giải:
Ta có: →AB=(-2-2;2-6) = (-4;-4) ⇒ AB = |→AB| = √(−4)2+(−4)2=4√2.
→AC=(8-2;0-6) = (6;-6) ⇒AC = |→AC|= √62+(−6)2=6√2.
Ta lại có: →AB.→AC= (-4).6+(-4).(-6) = 0
Nên →AB vuông góc với →AC hay tam giác ABC vuông tại A.
Vậy chọn đáp án B.
Bài 20 trang 67 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1; 5), B(- 1; - 1), C(2; - 5)
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trọng tâm G của tam giác ABC.
c) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD=32AB.
Lời giải:
a) Ta có: →AB=(-1-1;-1-5)= (-2;-6) và →AC= (2-1;-5-5) = (1;-10)
Ta thấy −21≠−6−10 nên →AB,→AC không cùng phương.
Vậy A, B, C không thẳng hàng.
b) Tọa độ trọng tâm G của tam giác ABC:
Vậy G(23;−13).
c) Do tứ giác ABCD là hình thang có AB // CD
Nên →AB và →CD ngược hướng
Mà CD=32 nên →CD=-32→AB
Gọi D(a; b), ta có: →AB=(-1-1;-1-5) = (-2;-6), →CD=(a-2b;b+5) .
Suy ra
Vậy D(5; 4).
Bài 21 trang 67 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 2; 4), B(- 5; - 1), C(8; - 2). Giải tam giác ABC (làm tròn các kết quả số đo góc đến hàng đơn vị).
Lời giải:
Ta có: →AB= (-5+2;-1-4) = (-3;-5)
→AC=(8+2;-2-4) = (10;-6)
→BC=(8+5;-2+1) = (13;-1)
Suy ra: AB=|→AB|=√(−3)2+(−5)2=√34
AC=|→AC|=√102+(−6)2=2√34
BC=|→BC|=√132+(−1)2=√170
Ta có: →AB.→AC= (-3).10+(-5).(-6) = 0 suy ra →AB vuông góc với →AC hay ^BAC=90o .
Ta có: cos(→AC,→BC)
= 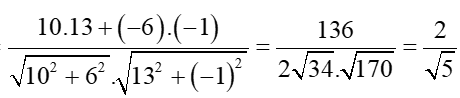
Suy ra ^ACB≈27o⇒^ABC=90o−^ACB≈63o.
Bài 22 trang 67 SBT Toán 10: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(4; - 2), B(10; 4) và điểm M nằm trên trục Ox. Tìm tọa độ điểm M sao cho |→MA+→MB| có giá trị nhỏ nhất.
Lời giải:
Do M nằm trên trục Ox nên M(a; 0).
Khi đó →MA= (4-a;-2) và →MB = (10-a;4).
⇒→MA+→MB= (14-2a;2)
⇒|→MA+→MB|=√(14−2a)2+22
Suy ra |→MA+→MB|2 = (14-2a)2 + 22≥22=4
Giá trị nhỏ nhất của |→MA+→MB|2 là 4
Hay giá trị nhỏ nhất của |→MA+→MB| là 2 đạt được khi 14 – 2a = 0⇔a=7
Vậy M(7; 0).
Bài 23 trang 67 SBT Toán 10: Trên màn hình ra đa của đài kiểm soát không lưu (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), một máy bay trực thăng chuyển động thẳng đều từ thành phố A có tọa độ (600; 200) đến thành phố B có tọa độ (200; 500) và thời gian bay quãng đường AB là 3 giờ. Hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.
Lời giải:
Gọi M(a; b) là tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.
Ta có: →AM=(a-600;b-200) và →AB=(-400;300)
Do máy bay chuyển động thẳng đều nên quãng đường máy bay đi được sau 1 giờ bằng 13 tổng quãng đường hay AM= 13AB .
Mà M thuộc đoạn AB nên →AM=13→AB .
Suy ra
Vậy M(14003;300) .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.