Với Giải SBT Toán 10 Tập 2 trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Sách bài tập Toán lớp 10 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.
Cho ba điểm A(- 2; 2), B(4; 2), C(6; 4). Viết phương trình đường thẳng ∆ đi qua B
Bài 45 trang 82 SBT Toán 10: Cho ba điểm A(- 2; 2), B(4; 2), C(6; 4). Viết phương trình đường thẳng ∆ đi qua B đồng thời cách đều A và C?
Lời giải:
cách đều A và C khi và chỉ khi ∆ đi qua trung điểm của AC hoặc ∆ song song với AC.
TH1: ∆ là đi qua trung điểm của AC
Gọi M là trung điểm của đoạn thẳng AB nên tọa độ điểm M là M(2; 3).
Vectơ chỉ phương của đường thẳng ∆ là: =(2;-1)
Suy ra vectơ pháp tuyến của đường thẳng ∆ là: =(1;2)
Do đó phương trình đường thẳng ∆ là: x – 2 + 2(y – 3) = 0 ⇔ x + 2y – 8 = 0
TH2: ∆ song song với AC.
Vectơ chỉ phương của đường thẳng ∆ là: =(8;2) nên vectơ pháp tuyến của đường thẳng ∆ là: =(1;-4)
Phương trình đường thẳng ∆ là: x – 4 – 4(y – 2) = 0 ⇔ x – 4y + 4 = 0.
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều với cuộc sống hay, chi tiết khác:
Bài 36 trang 81 SBT Toán 10: Đường thẳng ∆ đi qua điểm M(3; - 4) và vuông góc với đường thẳng d: x – 3y + 1 = 0 Bài 37 trang 81 SBT Toán 10: Cho ∆1: x – 2y + 3 = 0 và ∆2: – 2x – y + 5 = 0. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là:
Bài 38 trang 82 SBT Toán 10: Cho :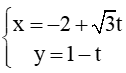
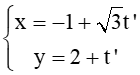
và :
. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là:
Bài 39 trang 82 SBT Toán 10: Khoảng cách từ điểm M(5; - 2) đến đường thẳng ∆: - 3x + 2y + 6 = 0 là:
Bài 40 trang 82 SBT Toán 10: Xét vị trí tương đối của mỗi cặp đường thẳng sau:
a) d1: 2x – 3y + 5 = 0 và d2: 2x + y – 1 = 0;
Bài 41 trang 82 SBT Toán 10: Tìm số đo góc giữa hai đường thẳng của mỗi cặp đường thẳng sau:
a) A(- 3; 1) và ∆1: 2x + y – 4 = 0;
Bài 44 trang 82 SBT Toán 10: Cho hai đường thẳng ∆1: mx – 2y – 1 = 0 và ∆2: x – 2y + 3 = 0.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
