Toptailieu biên soạn và giới thiệu giải Sách bài tập Toán 7 Bài tập cuối chương 4 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài tập cuối chương 4.
Giải SBT Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 4
Bài 1 trang 87 sách bài tập Toán 7: a) Đo các góc trong Hình 1; b) Nêu tên các cặp góc kề bù.
Lời giải:
a) Sử dụng thước đo góc ta đo được và
b) Các cặp góc kề bù có trong hình là: kề bù với kề bù với
Bài 2 trang 87 sách bài tập Toán 7: Hãy kể tên các cặp góc đối đỉnh trong Hình 2.
Lời giải:
a) Các cặp góc đối đỉnh trong hình là: và và
b) Các cặp góc đối đỉnh trong hình là: và ; và
c) Trong hình không có cặp góc nào đối đỉnh do chỉ có tia Oa là tia đối của tia Ob nhưng tia Oc không là tia đối của tia Od.
Bài 3 trang 87 sách bài tập Toán 7: Trong Hình 3 cho biết a // b. Tìm số đo các góc đỉnh A và B.
Lời giải:
– Tại đỉnh A:
• Vì và là hai góc đối đỉnh nên
• Vì và là hai góc kề bù nên ta có:
Suy ra
• Vì và là hai góc đối đỉnh nên
– Tại đỉnh B:
Vì a // b nên:
• (hai góc so le trong)
• (hai góc so le trong)
• (hai góc đồng vị)
• (hai góc đồng vị).
Vậy
Lời giải:
Hình vẽ minh họa:
Viết giả thiết và kết luận bằng kí hiệu:
a) Tìm góc đối đỉnh của góc M1.
b) Tìm góc kề bù của góc M1.
c) Tìm góc đồng vị của góc M3.
d) Tìm góc có số đo bằng số đo của góc M1.
Lời giải:
a) Góc đối đỉnh của là
b) Góc kề bù của là
c) Góc đồng vị của là
d) Các góc có số đo bằng số đo của là: (đối đỉnh) và (so le trong).
Lời giải:
Vì ABCD là hình thoi nên AB // CD và AD // BC.
Do AB // CD nên (hai góc so le trong)
Do AD // BC nên (hai góc so le trong)
Mà AC là tia phân giác của nên
Suy ra
Do đó CA là tia phân giác của
Vậy CA là tia phân giác của
Lời giải:
Hình vẽ minh họa:
Viết giả thiết và kết luận bằng kí hiệu:
Chứng minh định lí:
Vì nên AB ⊥ BC, AB ⊥ AD.
Do đó BC // AD (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song)
Mà nên BC ⊥ CD.
Ta có BC // AD và BC ⊥ CD.
Do đó AD ⊥ CD (một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại).
Suy ra
Vậy
Bài 8 trang 88 sách bài tập Toán 7: Quan sát hình 5, hãy chứng tỏ rằng xy⫽zt
Lời giải
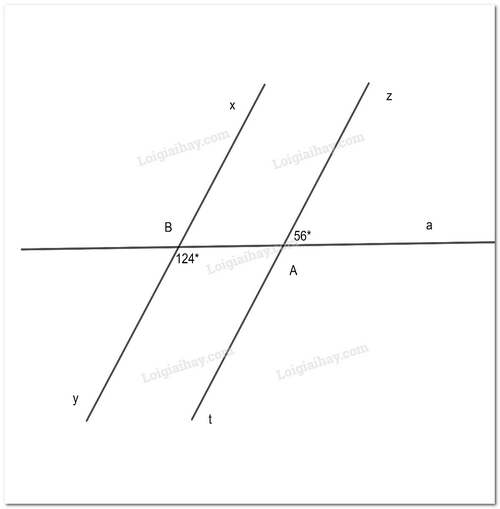
Gọi B là giao điểm của xy và a
Ta có :
Mà (2 góc kề bù)
Ta có:
Mà 2 góc này ở vị trí đồng vị nên xy⫽zt (Dấu hiệu nhận biết 2 đường thẳng song song)
Bài 9 trang 88 sách bài tập Toán 7: Quan sát Hình 6, hãy chứng tỏ rằng MN // EF.
Lời giải:
Vì và là hai góc kề nhau nên:
Suy ra
Vẽ tia Nx là tia đối của tia NF.
Khi đó và là hai góc kề bù nên:
Suy ra
Hay
Lại có nên
Mà và là hai góc ở vị trí đồng vị.
Do đó MN // EF.
Bài 10 trang 88 sách bài tập Toán 7: Quan sát Hình 7. a) Chứng minh rằng MN song song với RS
b) Cho . Tính
Phương pháp giải - Xem chi tiết
Sử dụng tính chất 2 đường thẳng song song
Lời giải
Ta có MNQP là hình chữ nhật (Tứ giác có 3 góc vuông)
(2 góc so le trong)
Vì (2 góc kề bù)
Ta thấy SR vuông góc với NR, MN vuông góc với NR do đó, MN // SR (2 góc so le trong)
Bài 11 trang 88 sách bài tập Toán 7: Quan sát Hình 8: a) Chứng minh rằng m // n.
a) Chứng minh rằng m // n.
b) Cho Tính
Lời giải:
a) Ta có m ⊥ d và n ⊥ d.
Do đó m // n (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song).
Vậy m // n.
b) Vì m // n nên (hai góc đồng vị).
Mà và là hai góc kề bù nên:
Suy ra
Vậy và
b) Nếu hai đường thẳng cùng tạo với một đường thẳng các góc so le trong bằng nhau thì .?.
Lời giải:
a) Nếu một đường thẳng cắt hai đường thẳng song song thì tạo thành các cặp góc đồng vị bằng nhau.
b) Nếu hai đường thẳng cùng tạo với một đường thẳng các góc so le trong bằng nhau thì hai đường thẳng đó song song với nhau.
b) Hai đường phân giác của hai góc kề bù thì .?.
Lời giải:
a) Hai góc cùng bù một góc thứ ba thì bằng nhau.
b) Hai đường phân giác của hai góc kề bù thì vuông góc.
a) Hãy vẽ hình minh họa định lí trên.
b) Viết giả thiết và kết luận của định lí.
c) Hãy chứng minh định lí trên.
Lời giải:
a) Hình vẽ minh họa:
b) Viết giả thiết và kết luận bằng kí hiệu:
c) Chứng minh định lí:
• Vì và là hai góc đối đỉnh nên
Mà (giả thiết)
Suy ra
Chứng minh tương tự ta có:
• Lại có và là hai góc kề bù nên:
Suy ra (1)
và là hai góc kề bù nên:
Suy ra (2)
Mà (3)
Từ (1), (2) và (3) suy ra
Chứng minh tương tự ta cũng có
Vậy định lí được chứng minh.
Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 4: Định lí và chứng minh định lí
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.