Toán 10 Chân trời sáng tạo trang 92 Bài 2: Tổng và hiệu của hai vecto

Toán 10 Chân trời sáng tạo trang 92 Bài 2: Tổng và hiệu của hai vecto

Giang Ngày: 10-02-2023 Lớp 10

279

Với giải Câu hỏi trang 92 Toán 10 Tập 1 Chân trời sáng tạo trong Bài 2: Tổng và hiệu của hai vecto giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 92 Bài 2: Tổng và hiệu của hai vecto

Thực hành 4 trang 92 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:

a) $\vec{a} = \vec{O B} - \vec{O D};$

b) $\vec{b} = (\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C})$ .

Phương pháp giải:

Bước 1: Thay thế vectơ bằng nhau rồi tìm tổng.

Bước 2: Tìm độ dài vectơ vừa tìm đc, độ dài vectơ $\vec{A B}$ là $| \vec{A B} | = A B$ .

Lời giải

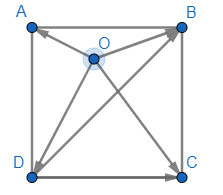
Thực hành 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Ta có: $A B = B C = C D = D A = 1;$

$A C = B D = \sqrt{A B^{2} + B C^{2}} = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$

a) $\vec{a} = \vec{O B} - \vec{O D} = \vec{O B} + \vec{D O} = (\vec{D O} + \vec{O B}) = \vec{D B}$

$\Rightarrow | \vec{a} | = | \vec{D B} | = D B = \sqrt{2}$

b) $\vec{b} = (\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C})$

$= (\vec{O C} + \vec{A O}) + (\vec{D B} + \vec{C D}) = (\vec{A O} + \vec{O C}) + (\vec{C D} + \vec{D B})$

$= \vec{A C} + \vec{C B} = \vec{A B}$

$\Rightarrow | \vec{b} | = | \vec{A B} | = A B = 1$

Chú ý khi giải:

Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại

4. TÍNH CHẤT VECTƠ CỦA TRUNG ĐIỂM VÀ TRỌNG TÂM

HĐ Khám phá 4 trang 92 Toán 10 Tập 1: a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết $\vec{M B} = - \vec{M A} = \vec{A M} .$ Hoàn thành phép cộng vectơ sau: $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = ?$

HĐ Khám phá 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 3)

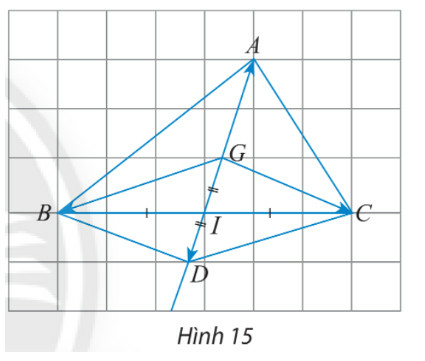
b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng $\vec{G B} + \vec{G C} = \vec{G D}$ và $\vec{G A} = \vec{D G}$ , hoàn thành các phép cộng vectơ sau:

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{G A} + \vec{G D} = \vec{D D} = ?$

HĐ Khám phá 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Phương pháp giải:

a) Thay thế các vectơ bằng nhau $\vec{M B} = - \vec{M A} = \vec{A M} .$

b) Bước 1: Áp dụng quy tắc hình bình hành trên BGCD

Bước 2: Áp dụng tính chất trung điểm vừa tìm được ở câu a) $\vec{M A} + \vec{M B} = \vec{0}$

(với M là trung điểm của AB)

Lời giải

a) $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = \vec{0}$ (vì vectơ $\vec{M B} = - \vec{M A} = \vec{A M} .$ )

b) Xét hình bình hành BGCD ta có: $\vec{G B} + \vec{G C} = \vec{G D}$

$\Rightarrow \vec{G A} + \vec{G B} + \vec{G C} = \vec{G A} + \vec{G D} = \vec{D G} + \vec{G D} = \vec{D D} = \vec{0}$

(vì $\vec{G A} = - \vec{G D} = \vec{D G}$ )

Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:

HĐ Khởi động trang 88 Toán 10 Tập 1: Một kiện hàng được vận chuyển từ điểm A đến điểm B

HĐ Khám phá 1 trang 88 Toán 10 Tập 1: Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ $\vec{A B}$ và $\vec{B C}$ (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên...

HĐ Khám phá 2 trang 89 Toán 10 Tập 1: Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: $\vec{A B} + \vec{A D} = \vec{A C}$ ...

Thực hành 1 trang 89 Toán 10 Tập 1: Cho hình thang ABCD có đáy là AB và CD. Cho biết $\vec{a} = \vec{A C} + \vec{C B}; \vec{b} = \vec{D B} + \vec{B C}$ . Chứng minh rằng hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng...

Thực hành 2 trang 89 Toán 10 Tập 1: Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ $\vec{A B} + \vec{A C}$ ...

Vận dụng 1 trang 90 Toán 10 Tập 1: Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên...

Vận dụng 2 trang 90 Toán 10 Tập 1: Hai người cùng kéo một con thuyền với hai lực $\vec{F_{1}} = \vec{O A}, \vec{F_{2}} = \vec{O B}$ có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là $60^{\circ}$ . Tìm độ lớn của vectơ hợp lực $\vec{F}$ là tổng của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$ ...

HĐ Khám phá 2 trang 90 Toán 10 Tập 1: Cho 3 vectơ $\vec{a}, \vec{b}, \vec{c}$ được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được...

Thực hành 3 trang 91 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau...

HĐ Khám phá 3 trang 91 Toán 10 Tập 1: Tìm hợp lực của hai lực đối nhau $\vec{F}$ và $- \vec{F}$ (hình 11)...

Thực hành 4 trang 92 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau...

HĐ Khám phá 4 trang 92 Toán 10 Tập 1: a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết $\vec{M B} = - \vec{M A} = \vec{A M} .$ Hoàn thành phép cộng vectơ sau: $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = ?$ ...

Thực hành 5 trang 93 Toán 10 Tập 1: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn...

Bài 1 trang 93 Toán 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng...

Bài 2 trang 93 Toán 10 Tập 1 Chân trời sáng tạo: Cho tứ giác ABCD, thực hiện cả phép cộng và trừ vectơ sau...

Bài 3 trang 93 Toán 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài các vectơ...

Bài 4 trang 93 Toán 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Chứng minh rằng...

Bài 5 trang 93 Toán 10 Tập 1: Cho ba lực $\vec{F_{1}} = \vec{M A}, \vec{F_{2}} = \vec{M B}$ và $\vec{F_{3}} = \vec{M C}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của $\vec{F_{1}}, \vec{F_{2}}$ đều là 10 N và $\hat{A M B} = 90^{\circ}$ Tìm độ lớn của lực $\vec{F_{3}}$ ...

Bài 6 trang 93 Toán 10 Tập 1: Khi máy bay nghiêng cánh một góc $α$ , lực $\vec{F}$ của không khí tác động vuông góc với cánh và bằng tổng của lực nâng $\vec{F_{1}}$ và lực cản $\vec{F_{2}}$ (Hình 16). Cho biết $α = 30^{\circ}$ và $| \vec{F} | = a$ . Tính $| \vec{F_{1}} |$ và $| \vec{F_{2}} |$ theo a...

Bài 7 trang 93 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn $\vec{K A} + \vec{K C} = \vec{0}; \vec{G A} + \vec{G B} + \vec{G C} = \vec{0}; \vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ . Tính độ dài các vectơ $\vec{K A}, \vec{G H}, \vec{A G}$ ...

Bài 8 trang 93 Toán 10 Tập 1: Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như hình 17. Tính độ dài vectơ tổng của hai vectơ nói trên...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

55

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

47

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

46

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

57

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.