Toán 10 Chân trời sáng tạo Bài 2: Tổng và hiệu của hai vectơ

Hoàng Huyền Trang Ngày: 10-02-2023 Lớp 10

753

Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2. Tổng và hiệu của hai vectơ sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo Bài 2: Tổng và hiệu của hai vectơ

1. TỔNG CỦA HAI VECTƠ

Câu hỏi trang 88 Toán 10

HĐ Khởi động trang 88 Toán 10 Tập 1: Một kiện hàng được vận chuyển từ điểm A đến điểm B

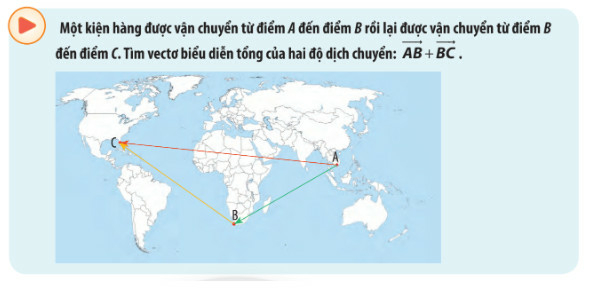
HĐ Khởi động trang 88 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Lời giải

$\vec{A B} + \vec{B C} = \vec{A C}$

HĐ Khám phá 1 trang 88 Toán 10 Tập 1: Một robot thực hiện liên tiếp hai chuyển động có độ dịch chuyển lần lượt được biểu diễn bởi 2 vectơ $\vec{A B}$ và $\vec{B C}$ (Hình 1). Tìm vectơ biểu diễn sự dịch chuyển của rô bốt sau hai sự dịch chuyển trên.

Phương pháp giải:

Xác định A là điểm đầu và C là điểm cuối, dùng đoạn thẳng có hướng nối 2 điểm trên.

Lời giải

Ta thấy rô bốt đi từ A đến B, sau đó đi từ B đến C, vậy cả 2 lần di chuyển thì ta thấy điểm cuất phát là A và điểm kết thúc là C.

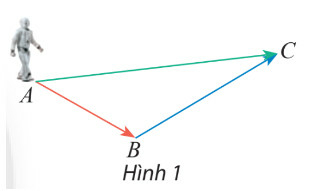
HĐ Khám phá 1 trang 88 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Suy ra vectơ biểu diễn sự dịch chuyển của rô bốt sau hai lần dịch chuyển là vectơ $\vec{A C}$

HĐ Khám phá 2 trang 89 Toán 10 Tập 1: Cho hình bình hành ABCD (Hình 4). Chứng minh rằng: $\vec{A B} + \vec{A D} = \vec{A C}$

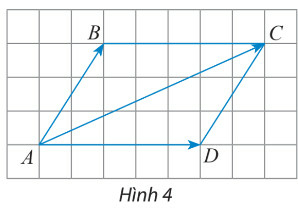
HĐ Khám phá 2 trang 89 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Tìm vectơ bằng với vectơ $\vec{A D}$ , sau đó áp dụng quy tắc ba điểm

Lời giải

Vì ABCD là hình bình hành nên ta có: $\vec{A D} = \vec{B C}$ $\vec{A B} + \vec{A D} = \vec{A B} + \vec{B C} = \vec{A C}$ (đpcm)

Câu hỏi trang 89 Toán 10

Thực hành 1 trang 89 Toán 10 Tập 1: Cho hình thang ABCD có đáy là AB và CD. Cho biết $\vec{a} = \vec{A C} + \vec{C B}; \vec{b} = \vec{D B} + \vec{B C}$ . Chứng minh rằng hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.

Phương pháp giải:

Bước 1: Áp dụng quy tắc ba điểm, tìm vectơ $\vec{a}$ và $\vec{b}$

Bước 2: Xác định hướng của vectơ vừa tìm được

Bước 3: So sánh hướng của 2 vectơ

Lời giải

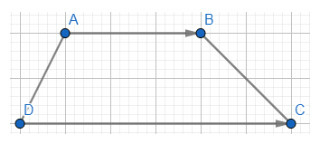
Thực hành 1 trang 89 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Áp dụng quy tắc ba điểm ta có:

$\vec{a} = \vec{A C} + \vec{C B} = \vec{A B}$ ; $\vec{b} = \vec{D B} + \vec{B C} = \vec{D C}$

Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ $\vec{A B}$ và vectơ $\vec{D C}$ đều có hướng từ trái sang phải, suy ra vectơ $\vec{A B}$ và vectơ $\vec{D C}$ cùng hướng

Vậy hai vectơ $\vec{a}$ và $\vec{b}$ cùng hướng.

Thực hành 2 trang 89 Toán 10 Tập 1: Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ $\vec{A B} + \vec{A C}$

Phương pháp giải:

Bước 1: Dựng hình bình hành ABDC

Bước 2: Áp dụng quy tắc hình bình hành tìm tổng vectơ $\vec{A B} + \vec{A C}$

Bước 3: Tìm độ dài vectơ tổng.

Lời giải

Dựng hình bình hành ABDC.

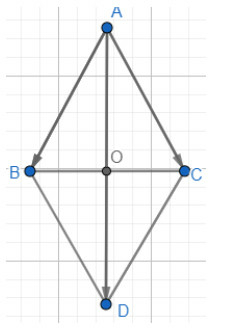
Thực hành 2 trang 89 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Áp dụng quy tắc hình bình hành vào ABDC ta có:

$\vec{A B} + \vec{A C} = \vec{A D} \Rightarrow | \vec{A B} + \vec{A C} | = | \vec{A D} | = A D$

Gọi O là giao điểm của AD và BC, ta có:

$A O = \sqrt{A B^{2} - B O^{2}} = \sqrt{A B^{2} - {(\frac{1}{2} B C)}^{2}} = \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = \frac{a \sqrt{3}}{2}$

$A D = 2 A O = a \sqrt{3} \Rightarrow | \vec{A B} + \vec{A C} | = a \sqrt{3}$

Vậy độ dài vectơ $\vec{A B} + \vec{A C}$ là $a \sqrt{3}$

Câu hỏi trang 90 Toán 10

Vận dụng 1 trang 90 Toán 10 Tập 1: Một máy bay có vận tốc chỉ theo hướng bắc, vận tốc gió là một vectơ theo hướng đông như hình 7. Tính độ dài vectơ tổng của hai vectơ nói trên.

Vận dụng 1 trang 90 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải:

Bước 1: Áp dụng quy tắc 3 điểm để tìm vectơ tổng

Bước 2: Tìm độ dài vectơ tổng vừa tìm được.

Lời giải

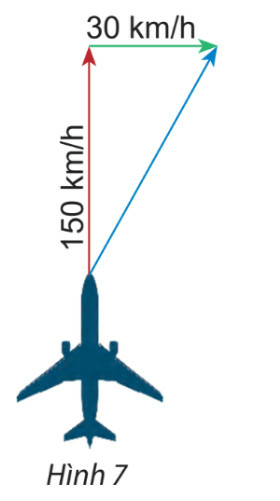
Gọi vectơ chỉ vận tốc của máy bay là vectơ $\vec{A B}$ và vectơ chỉ vận tốc của gió là vectơ $\vec{B C}$ .

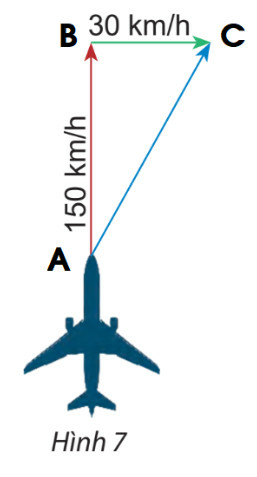
Vận dụng 1 trang 90 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Ta có: $\vec{A B} + \vec{B C} = \vec{A C}$

Áp dụng định lý Pitago ta có:

$A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{150^{2} + 30^{2}} = 30 \sqrt{26}$

Vậy độ dài vectơ tổng của hai vectơ nói trên là $30 \sqrt{26}$ km/h

Vận dụng 2 trang 90 Toán 10 Tập 1: Hai người cùng kéo một con thuyền với hai lực $\vec{F_{1}} = \vec{O A}, \vec{F_{2}} = \vec{O B}$ có độ lớn lần lượt là 400 N, 600 N (hình 8). Cho biết góc giữa hai vectơ là $60^{\circ}$ . Tìm độ lớn của vectơ hợp lực $\vec{F}$ là tổng của hai lực $\vec{F_{1}}$ và $\vec{F_{2}}$

Vận dụng 2 trang 90 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

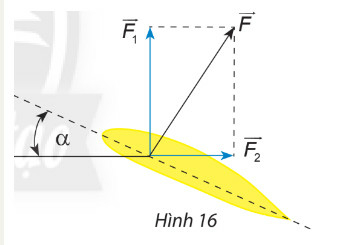
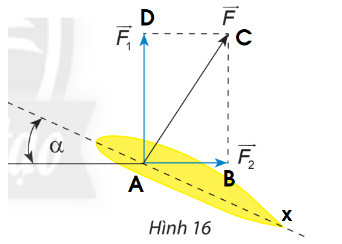
Phương pháp giải:

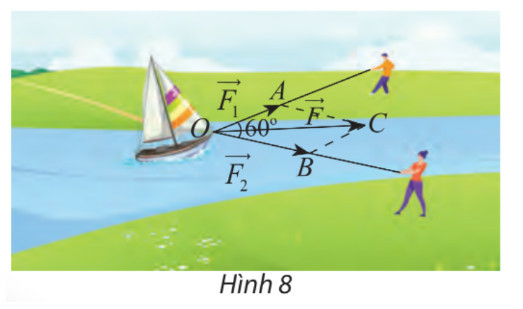
Bước 1: Dựng hình bình hành AOBC

Bước 2: Áp dụng quy tắc hình bình hành tìm tổng lực

Bước 3: Xác định độ lớn của vectơ tổng.

Lời giải

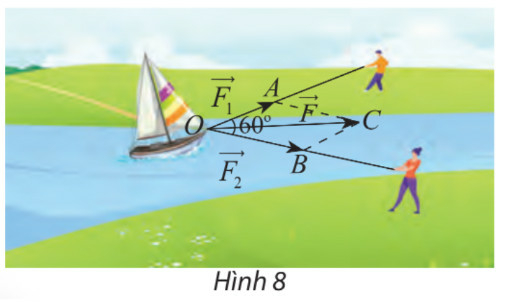
Vận dụng 2 trang 90 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 3)

Áp dụng quy tắc hình bình hành ta có: $\vec{F} = \vec{F_{1}} + \vec{F_{2}} = \vec{O A} + \vec{O B} = \vec{O C}$ ;

$A C = O B = 600$ ; $\hat{A O B} = 60^{\circ} \Rightarrow \hat{O A C} = 120^{\circ}$ (hai góc bù nhau trong hình bình hành).

Áp dụng định lý cos ta có:

$O C = \sqrt{O A^{2} + A C^{2} - 2 O A . A C . \cos (120^{\circ})}$

$= \sqrt{400^{2} + 600^{2} - 2.400.600. \cos (120^{\circ})} ≃ 871, 78$ N

Vậy độ lớn của vectơ hợp lực $\vec{F}$ gần bằng 871,78 N

2. TÍNH CHẤT CỦA PHÉP CỘNG CÁC VECTƠ

HĐ Khám phá 2 trang 90 Toán 10 Tập 1: Cho 3 vectơ $\vec{a}, \vec{b}, \vec{c}$ được biểu diễn như hình 9. Hãy hoàn thành các phép cộng vectơ sau và so sánh kết quả tìm được:

a) $\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = ?$

$\vec{b} + \vec{a} = \vec{A E} + \vec{E C} = ?$

b) $(\vec{a} + \vec{b}) + \vec{c} = (\vec{A B} + \vec{B C}) + \vec{C D} = \vec{A C} + \vec{C D} = ?$

$\vec{a} + (\vec{b} + \vec{c}) = \vec{A B} + (\vec{B C} + \vec{C D}) = \vec{A B} + \vec{B D} = ?$

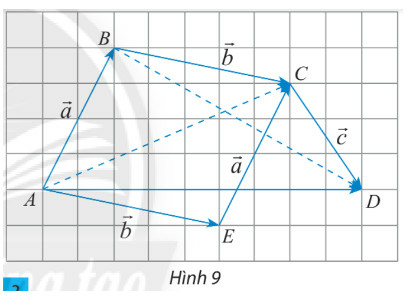
HĐ Khám phá 2 trang 90 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Phương pháp giải:

Bước 1: Áp dụng quy tắc 3 điểm: $\vec{A B} + \vec{B C} = \vec{A C}$ ;

Bước 2: So sánh các vectơ vừa tìm được

Lời giải

a) Áp dụng quy tắc ba điểm ta có:

$\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = \vec{A C}$ ; $\vec{b} + \vec{a} = \vec{A E} + \vec{E C} = \vec{A C}$

$\Rightarrow \vec{a} + \vec{b} = \vec{b} + \vec{a}$

a) Áp dụng quy tắc ba điểm ta có:

$(\vec{a} + \vec{b}) + \vec{c} = (\vec{A B} + \vec{B C}) + \vec{C D} = \vec{A C} + \vec{C D} = \vec{A D}$

$\vec{a} + (\vec{b} + \vec{c}) = \vec{A B} + (\vec{B C} + \vec{C D}) = \vec{A B} + \vec{B D} = \vec{A D}$

$\Rightarrow (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$

Câu hỏi trang 91 Toán 10

Thực hành 3 trang 91 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng 1. Tính độ dài các vectơ sau:

a) $\vec{a} = (\vec{A C} + \vec{B D}) + \vec{C B};$

b) $\vec{a} = \vec{A B} + \vec{A D} + \vec{B C} + \vec{D A} .$

Phương pháp giải:

Bước 1: Sử dụng tính chất giao hoán, kết hợp, cộng với vectơ $\vec{0}$ tìm tổng các vectơ

Bước 2: Tính độ dài vectơ vừa tìm đc, độ dài vectơ $\vec{A B}$ là \(\left|

Lời giải

a) $\begin{array}{l} \vec{a} = (\vec{A C} + \vec{B D}) + \vec{C B} = (\vec{A C} + \vec{C B}) + \vec{B D} \\ = \vec{A B} + \vec{B D} = \vec{A D} \Rightarrow | \vec{A D} | = A D = 1 \end{array}$

b) $\begin{array}{l} \vec{a} = \vec{A B} + \vec{A D} + \vec{B C} + \vec{D A} = (\vec{A B} + \vec{B C}) + (\vec{A D} + \vec{D A}) \\ = \vec{A C} + \vec{A A} = \vec{A C} + \vec{0} = \vec{A C} \end{array}$

$A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$

$\Rightarrow | \vec{A C} | = \sqrt{2}$

3. HIỆU CỦA HAI VECTƠ

HĐ Khám phá 3 trang 91 Toán 10 Tập 1: Tìm hợp lực của hai lực đối nhau $\vec{F}$ và $- \vec{F}$ (hình 11)

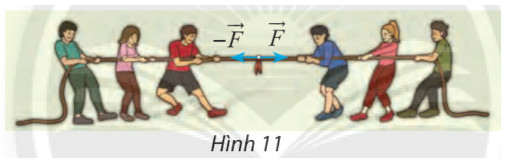
HĐ Khám phá 3 trang 91 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Lời giải

$\vec{F} + (- \vec{F}) = \vec{F} - \vec{F} = \vec{0}$

Câu hỏi trang 92 Toán 10

Thực hành 4 trang 92 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:

a) $\vec{a} = \vec{O B} - \vec{O D};$

b) $\vec{b} = (\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C})$ .

Phương pháp giải:

Bước 1: Thay thế vectơ bằng nhau rồi tìm tổng.

Bước 2: Tìm độ dài vectơ vừa tìm đc, độ dài vectơ $\vec{A B}$ là $| \vec{A B} | = A B$ .

Lời giải

Thực hành 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Ta có: $A B = B C = C D = D A = 1;$

$A C = B D = \sqrt{A B^{2} + B C^{2}} = \sqrt{1^{2} + 1^{2}} = \sqrt{2}$

a) $\vec{a} = \vec{O B} - \vec{O D} = \vec{O B} + \vec{D O} = (\vec{D O} + \vec{O B}) = \vec{D B}$

$\Rightarrow | \vec{a} | = | \vec{D B} | = D B = \sqrt{2}$

b) $\vec{b} = (\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C})$

$= (\vec{O C} + \vec{A O}) + (\vec{D B} + \vec{C D}) = (\vec{A O} + \vec{O C}) + (\vec{C D} + \vec{D B})$

$= \vec{A C} + \vec{C B} = \vec{A B}$

$\Rightarrow | \vec{b} | = | \vec{A B} | = A B = 1$

Chú ý khi giải:

Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại

4. TÍNH CHẤT VECTƠ CỦA TRUNG ĐIỂM VÀ TRỌNG TÂM

HĐ Khám phá 4 trang 92 Toán 10 Tập 1: a) Cho điểm M là trung điểm của đoạn thẳng AB. Ta đã biết $\vec{M B} = - \vec{M A} = \vec{A M} .$ Hoàn thành phép cộng vectơ sau: $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = ?$

HĐ Khám phá 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 3)

b) Cho điểm G là trọng tâm của tam giác ABC có trung tuyến AI. Lấy D là điểm đối xứng với G qua I. Ta có BGCD là hình bình hành và G là trung điểm của đoạn thẳng AD. Với lưu ý rằng $\vec{G B} + \vec{G C} = \vec{G D}$ và $\vec{G A} = \vec{D G}$ , hoàn thành các phép cộng vectơ sau:

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{G A} + \vec{G D} = \vec{D D} = ?$

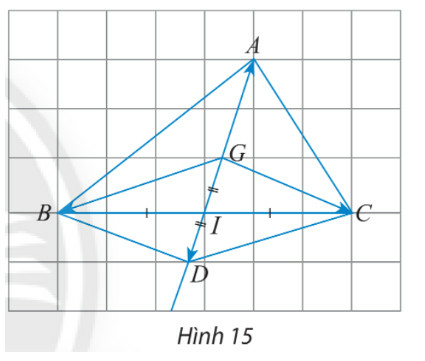
HĐ Khám phá 4 trang 92 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Phương pháp giải:

a) Thay thế các vectơ bằng nhau $\vec{M B} = - \vec{M A} = \vec{A M} .$

b) Bước 1: Áp dụng quy tắc hình bình hành trên BGCD

Bước 2: Áp dụng tính chất trung điểm vừa tìm được ở câu a) $\vec{M A} + \vec{M B} = \vec{0}$

(với M là trung điểm của AB)

Lời giải

a) $\vec{M A} + \vec{M B} = \vec{M A} + \vec{A M} = \vec{M M} = \vec{0}$ (vì vectơ $\vec{M B} = - \vec{M A} = \vec{A M} .$ )

b) Xét hình bình hành BGCD ta có: $\vec{G B} + \vec{G C} = \vec{G D}$

$\Rightarrow \vec{G A} + \vec{G B} + \vec{G C} = \vec{G A} + \vec{G D} = \vec{D G} + \vec{G D} = \vec{D D} = \vec{0}$

(vì $\vec{G A} = - \vec{G D} = \vec{D G}$ )

Câu hỏi trang 93 Toán 10

Thực hành 5 trang 93 Toán 10 Tập 1: Cho hình bình hành ABCD có tâm O. Tìm ba điểm M, N, P thỏa mãn:

a) $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$

b) $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$

c) $\vec{P M} + \vec{P N} = \vec{0}$

Phương pháp

a) Sử dụng tính chất trọng tâm của tam giác $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ (với G là trọng tâm của tam giác ABC)

b) Sử dụng tính chất trọng tâm của tam giác $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

c) Sử dụng tính chất trung điểm $\vec{M A} + \vec{M B} = \vec{0}$ (với M là trung điểm của AB)

Phương pháp giải:

a) Sử dụng tính chất trọng tâm của tam giác $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ (với G là trọng tâm của tam giác ABC)

b) Sử dụng tính chất trọng tâm của tam giác $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

c) Sử dụng tính chất trung điểm $\vec{M A} + \vec{M B} = \vec{0}$ (với M là trung điểm của AB)

Lời giải

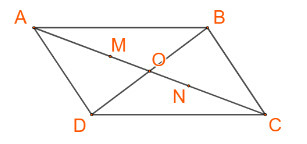
Thực hành 5 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) Áp dụng tính chất trọng tâm ta có: $\vec{M A} + \vec{M D} + \vec{M B} = \vec{0}$

Suy ra M là trọng tâm của tam giác ADB

Vậy M nằm trên đoạn thẳng AO sao cho $A M = \frac{2}{3} A O$

b) Tiếp tục áp dụng tính chất trọng tâm $\vec{N D} + \vec{N B} + \vec{N C} = \vec{0}$

Suy ra N là trọng tâm của tam giác BCD

Vậy N nằm trên đoạn thẳng OD sao cho $O N = \frac{1}{3} O D$

c) Áp dụng tính chất trung điểm ta có: $\vec{P M} + \vec{P N} = \vec{0}$

Suy ra P là trung điểm của đoạn thẳng MN

Vậy điểm P trùng với điểm O

Bài tập

Bài 1 trang 93 Toán 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:

a) $\vec{B A} + \vec{D C} = \vec{0;}$

b) $\vec{M A} + \vec{M C} = \vec{M B} + \vec{M D}$

Phương pháp giải

a) Thay vectơ $\vec{D C} = \vec{A B}$

b) Bước 1: chèn điểm O: $\vec{A B} = \vec{A O} + \vec{O B}$

Bước 2: Sử dụng tính chất trung điểm: $\vec{M A} + \vec{M B} = \vec{0}$ (với M là trung điểm của đoạn thẳng AB)

Lời giải

a) ABCD là hình bình hành nên $\vec{D C} = \vec{A B}$

$\Rightarrow \vec{B A} + \vec{D C} = \vec{B A} + \vec{A B} = \vec{B B} = \vec{0}$

b) $\vec{M A} + \vec{M C} = (\vec{M B} + \vec{B A}) + (\vec{M D} + \vec{D C})$

$= (\vec{M B} + \vec{M D}) + (\vec{B A} + \vec{D C})$

$= \vec{M B} + \vec{M D}$ (Vì $\vec{B A} + \vec{D C} = \vec{0}$ )

Bài 2 trang 93 Toán 10 Tập 1: Cho tứ giác ABCD, thực hiện cả phép cộng và trừ vectơ sau:

a) $\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A}$ ;

b) $\vec{A B} - \vec{A D}$

c) $\vec{C B} - \vec{C D}$ .

Lời giải

a) $\vec{A B} + \vec{B C} + \vec{C D} + \vec{D A} = (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D A}) = \vec{A C} + \vec{C A} = \vec{A A} = \vec{0}$

b) $\vec{A B} - \vec{A D} = \vec{A B} + \vec{D A} = \vec{D A} + \vec{A B} = \vec{D B}$

c) $\vec{C B} - \vec{C D} = \vec{C B} + \vec{D C} = \vec{D C} + \vec{C B} = \vec{D B}$

Bài 3 trang 93 Toán 10 Tập 1: Cho tam giác đều ABC cạnh bằng a. Tính độ dài các vectơ:

a) $\vec{B A} + \vec{A C}$ ;

b) $\vec{A B} + \vec{A C}$ ;

c) $\vec{B A} - \vec{B C}$ .

Phương pháp giải

a) Sử dụng quy tắc ba điểm $\vec{A B} + \vec{B C} = \vec{A C}$

Bước 1: Dựng hình bình hành ABDC, xác định giao điểm của 2 đường chéo là điểm O.

Bước 2: Xác định vectot tổng $\vec{A B} + \vec{A C} = ?$

Bước 3: Tính độ dài của vecto tìm được

Bước 1: Thay thế vecto đối $\vec{A B} = - \vec{B A}$

Bước 2: Sử dụng quy tắc ba điểm tính vecto tổng

Bước 3: Tính độ dài

Lời giải

a) $\vec{B A} + \vec{A C} = \vec{B C} \Rightarrow | \vec{B C} | = B C = a$

b) Dựng hình bình hành ABDC, giao điểm của hai đường chéo là O ta có:

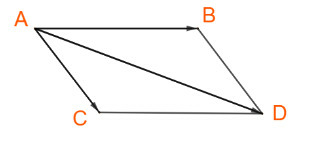
Bài 3 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

$\vec{A B} + \vec{A C} = \vec{A D}$

$A D = 2 A O = 2 \sqrt{A B^{2} - B O^{2}} = 2 \sqrt{a^{2} - {(\frac{a}{2})}^{2}} = a \sqrt{3}$

$\Rightarrow | \vec{A B} + \vec{A C} | = | \vec{A D} | = A D = a \sqrt{3}$

c) $\vec{B A} - \vec{B C} = \vec{B A} + \vec{C B} = \vec{C B} + \vec{B A} = \vec{C A}$

$\Rightarrow | \vec{B A} - \vec{B C} | = | \vec{C A} | = C A = a$

Bài 4 trang 93 Toán 10 Tập 1: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Chứng minh rằng:

a) $\vec{O A} - \vec{O B} = \vec{O D} - \vec{O C;}$

b) $\vec{O A} - \vec{O B} + \vec{D C} = \vec{0}$

Phương pháp giải

Vận dụng quy tắc hiệu: $\vec{O A} - \vec{O B} = \vec{B A}$

Lời giải

a) $\vec{O A} - \vec{O B} = \vec{B A}$

$\vec{O D} - \vec{O C} = \vec{C D}$

Do ABCD là hình bình hành nên $\vec{B A} = \vec{C D}$

Suy ra, $\vec{O A} - \vec{O B} = \vec{O D} - \vec{O C}$

b) $\vec{O A} - \vec{O B} + \vec{D C} = (\vec{O D} - \vec{O C}) + \vec{D C} = \vec{C D} + \vec{D C} = \vec{C C} = \vec{0}$

Bài 5 trang 93 Toán 10 Tập 1: Cho ba lực $\vec{F_{1}} = \vec{M A}, \vec{F_{2}} = \vec{M B}$ và $\vec{F_{3}} = \vec{M C}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của $\vec{F_{1}}, \vec{F_{2}}$ đều là 10 N và $\hat{A M B} = 90^{\circ}$ Tìm độ lớn của lực $\vec{F_{3}}$ .

Lời giải

Ba lực $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ cùng tác dụng vào M và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay: $\vec{F_{1}} + \vec{F_{2}} + \vec{F_{3}} = \vec{M A} + \vec{M B} + \vec{M C} = \vec{0}$

Dựng hình bình hành $M A D B$ , khi đó: $\vec{M A} + \vec{M B} = \vec{M D}$

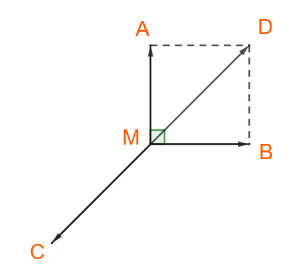
Bài 5 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

$\Rightarrow \vec{M D} + \vec{M C} = \vec{0}$

$\Rightarrow \vec{M D}, \vec{M C}$ là hai vecto đối nhau

$\Rightarrow M D = M C$

Xét hình bình hành MADB, ta có:

AM=AB và $\hat{A M B} = 90^{\circ}$

$\Rightarrow$ MADB là hình vuông, cạnh $A B = 10$

$\Rightarrow M C = M D = A B . \sqrt{2} = 10 \sqrt{2}$

Vậy độ lớn của lực $\vec{F_{3}}$ là $| \vec{F_{3}} | = | \vec{M C} | = M C = 10 \sqrt{2}$ (N)

Bài 6 trang 93 Toán 10 Tập 1: Khi máy bay nghiêng cánh một góc $α$ , lực $\vec{F}$ của không khí tác động vuông góc với cánh và bằng tổng của lực nâng $\vec{F_{1}}$ và lực cản $\vec{F_{2}}$ (Hình 16). Cho biết $α = 30^{\circ}$ và $| \vec{F} | = a$ . Tính $| \vec{F_{1}} |$ và $| \vec{F_{2}} |$ theo a.

Bài 6 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Lời giải

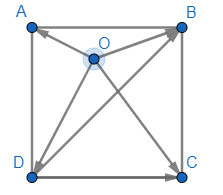
Kí hiệu các điểm như hình dưới.

Bài 6 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Khi đó các lực $\vec{F}, \vec{F_{1}}, \vec{F_{2}}$ lần lượt là $\vec{A C}, \vec{A D}, \vec{A B}$

$α = \hat{B A x} = 30^{\circ}$ $\Rightarrow \hat{C A B} = 60^{\circ}$

$A B = A C . c o s \hat{C A B} = a . c {o s 60}^{\circ} = \frac{a}{2} \Rightarrow | \vec{F_{2}} | = | \vec{A B} | = \frac{a}{2}$

$A D = B C = A C . \sin \hat{C A B} = a . \sin 60^{\circ} = \frac{a \sqrt{3}}{2} \Rightarrow | \vec{F_{1}} | = | \vec{A D} | = A D = \frac{a \sqrt{3}}{2}$

Vậy $| \vec{F_{1}} | = \frac{a \sqrt{3}}{2}; | \vec{F_{2}} | = \frac{a}{2}$

Bài 7 trang 93 Toán 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn $\vec{K A} + \vec{K C} = \vec{0}; \vec{G A} + \vec{G B} + \vec{G C} = \vec{0}; \vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ . Tính độ dài các vectơ $\vec{K A}, \vec{G H}, \vec{A G}$ .

Lời giải

Ta có $A C = A B \sqrt{2} = a \sqrt{2}$

+) $\vec{K A} + \vec{K C} = \vec{0}$ ,

Suy ra K là trung điểm AC $\Rightarrow A K = \frac{1}{2} . a \sqrt{2} = \frac{a \sqrt{2}}{2}$

+) $\vec{H A} + \vec{H D} + \vec{H C} = \vec{0}$ , suy ra H là trọng tâm của tam giác ADC

$\Rightarrow D H = \frac{2}{3} D K = \frac{1}{3} D B$ (1)

+) $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ , suy ra G là trọng tâm của tam giác ABC

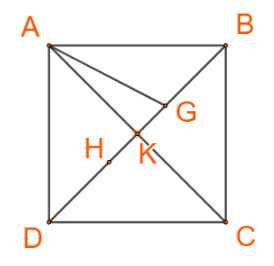
Bài 7 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

$\Rightarrow B G = \frac{2}{3} B K = \frac{1}{3} B D$ (2)

$(1, 2) \Rightarrow H G = \frac{1}{3} B D = \frac{a \sqrt{2}}{3}$

Mà $K G = K H = \frac{1}{2} H G = \frac{a \sqrt{2}}{6}$ (2)

$\Rightarrow A G = \sqrt{A K^{2} + G K^{2}} = \sqrt{{(\frac{a \sqrt{2}}{2})}^{2} + {(\frac{a \sqrt{2}}{6})}^{2}} = \frac{a \sqrt{5}}{3}$

$\Rightarrow | \vec{A G} | = \frac{a \sqrt{5}}{3}$

Vậy $| \vec{K A} | = \frac{a \sqrt{2}}{2}, | \vec{G H} | = \frac{a \sqrt{2}}{3}, | \vec{A G} | = \frac{a \sqrt{5}}{3}$ .

Bài 8 trang 93 Toán 10 Tập 1: Một con tàu có vectơ vận tốc chỉ theo hướng nam, vận tốc của dòng nước là một vectơ theo hướng đông như hình 17. Tính độ dài vectơ tổng của hai vectơ nói trên.

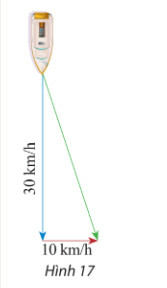
Bài 7 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Lời giải

Gọi vecto vận tốc của tàu là $\vec{A B}$ , vecto vận tốc của dòng nước là vecto $\vec{B C}$

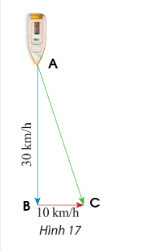
Bài 7 trang 93 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Ta có vecto tổng là $\vec{F} = \vec{A B} + \vec{B C} = \vec{A C}$

Độ dài vecto tổng là $| \vec{F} | = | \vec{A C} | = A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{30^{2} + 10^{2}} = 10 \sqrt{10}$ (km/h)

Vậy độ dài vecto tổng là $10 \sqrt{10}$ (km/h).

Lý thuyết Bài 2. Tổng và hiệu của hai vectơ

1. TỔNG CỦA HAI VECTƠ

Quy tắc ba điểm:

Với 3 điểm M, N, P ta có: $\vec{M N} + \vec{N P} = \vec{M P}$

Quy tắc hình bình hành:

Nếu OABC là hình bình hành thì ta có $\vec{O A} + \vec{O C} = \vec{O B}$

2. TÍNH CHẤT CỦA PHÉP CỘNG CÁC VECTƠ

Phép cộng vecto có các tính chất sau:

Tính chất giao hoán: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$

Tính chất kết hợp: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$

Với mọi vecto $\vec{a},$ ta luôn có: $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$

Chú ý: $\vec{a} + (- \vec{a}) = \vec{0}$ (Tổng hai vecto đối luôn bằng vecto-không)

3. HIỆU CỦA HAI VECTƠ

+) Hiệu của hai vecto $\vec{a} - \vec{b} = \vec{a} + (- \vec{b})$

Chú ý: Cho ba điểm O, A, B ta có: $\vec{O B} - \vec{O A} = \vec{A B}$

4. TÍNH CHẤT VECTƠ CỦA TRUNG ĐIỂM VÀ TRỌNG TÂM

+) M là trung điểm AB $\Leftrightarrow \vec{M A} + \vec{M B} = \vec{0}$

+) G là trọng tâm của $Δ A B C$ $\Leftrightarrow \vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

295

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

315

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

344

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

291