Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 1. Khái niệm vectơ sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 1. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Chân trời sáng tạo Bài 1: Khái niệm vectơ
Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Khối lượng của hàng: 500 tấn
- Độ dịch chuyển của tàu: 500km từ A đến B
Lời giải
Sự khác biệt là:
- Đơn vị đo: tấn và 500.
- Khối lượng hàng là đại lượng chỉ có độ lớn (500 tấn), còn độ dịch chuyển của tàu là đại lượng có cả độ lớn (500 km) và hướng (từ A đến B).
Phương pháp giải:
Vectơ →AB có điểm đầu là A, điểm cuối là B và có giá là đường thẳng AB
Lời giải
Vectơ →CHcó điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.
Vectơ →CB có điểm đầu là C, điểm cuối là B và có giá là đường thẳng CB
Vectơ →HA có điểm đầu là H, điểm cuối là A và có giá là đường thẳng HA
Ta có: CH=12CB=1, CB=2, AH=√AC2−HC2=√22−12=√3.
Suy ra: |→CH|=1, |→CB|=2, |→HA|=√3
Phương pháp giải:
Độ dài vectơ →AC là |→AC|=AC
Lời giải
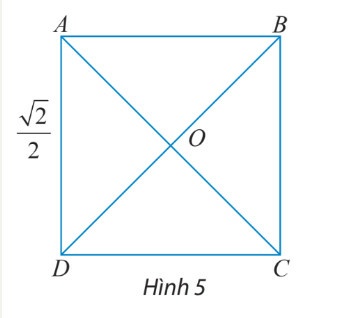
Ta có: AC=BD=√AD2+DC2=√(√22)2+(√22)2=1
OA=12AC=12
Suy ra: |→AC|=1, |→BD|=1, |→OA|=1, |→AO|=1
2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
Lời giải
Ta có: giá của →AB là đường thẳng AB, giá của →CDlà đường thẳng CD, và thấy rằng 2 đường thẳng này trùng nhau suy ra giá của 2 vecto này trùng nhau.
Tương tự ta thấy giá của cặp →PQ và →RS song song với nhau.
Thực hành 3 trang 84 Toán 10 Tập 1: Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ →x;
b) Cùng hướng với vectơ →a ;
Ngược hướng với vectơ →u.
Phương pháp giải:
a) Xác định các vectơ có giá song song hoặc trùng với giá của vectơ x
b) Xác định các vectơ cùng phương, cùng chiều với vectơ a
c) Xác định các vectơ cùng phương, ngược chiều với vectơ u
Lời giải
a) Ta có:
Giá của vectơ →w trùng với giá của →x
Giá của vectơ →y, →zsong song với giá của →x
Suy ra các vectơ cùng phương với vectơ →x là →w, →yvà →z
b) Ta có:
Vectơ →b có giá song song với vectơ →avà có cùng hướng từ trên xuống với vectơ →anên vectơ →b cùng hướng với vectơ →a
c) Ta có:
Vectơ →v có giá song song với vectơ →uvà ngược hướng từ dưới lên trên so với vectơ →unên vectơ →v ngược hướng với vectơ →u
Thực hành 4 trang 84 Toán 10 Tập 1: Khẳng định sau đây đúng hay sai? Hãy giải thích.
Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ →AB và →ACcùng hướng.
Phương pháp giải:
Thay đổi các vị trí của 3 điểm, kiểm tra hai vectơ →AB và →AC có cùng hướng hay không.
Lời giải
Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ →AB và →AC cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
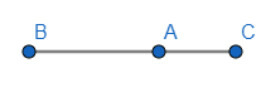
Khi A nằm giữa B và C thì hướng của vectơ →AB là từ phải sang trái, còn hướng của vectơ →AClà từ trái sang phải nên hai vectơ này là ngược hướng.
3. HAI VECTƠ BẰNG NHAU - VECTƠ ĐỐI NHAU
a) →AB và →DC
b) →AD và →CB
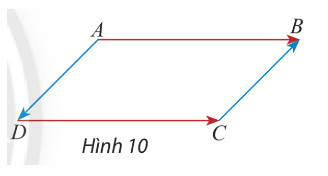
Lời giải
a) Ta có: AB=CD⇒|→AB|=|→CD|
AB//CD và →AB, →DC có hướng từ trái sang phải
Suy ra →AB và →DC cùng hướng
b) Ta có: AD=CB⇒|→AD|=|→CB|
AD//CB và →ADcó hướng từ trên xuống dưới, →CB có hướng từ dưới lên trên. Suy ra →AD và →CB ngược hướng
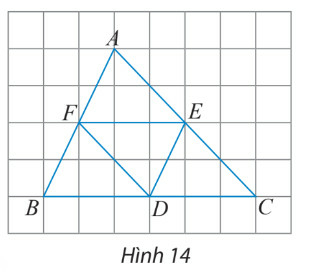
a) Tìm các vectơ bằng vectơ →EF.
b) Tìm các vectơ đối vectơ →EC
Phương pháp giải:
a)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ →EF
Bước 2: Trong đó liệt kê các vectơ cùng hướng với vectơ →EF
b)
Bước 1: Từ H14, xác định các đoạn thẳng có độ dài bằng độ dài vectơ →EC
Bước 2: Trong đó liệt kê các vectơ ngược hướng với vectơ →EC
Lời giải
Từ giả thiết ta có:
AF=FB=ED; AE=EC=FD; BD=DC=EF
Từ đó dựa vào hình ta có:
a) Các vectơ bằng vectơ →EFlà →BD và →DC
b) Các vectơ đối vectơ →EC là →EA và →DF
4. VECTƠ - KHÔNG
Thực hành 6 trang 86 Toán 10 Tập 1: Tìm các độ dài của các vectơ →EF,→EE,→EM,→MM,→FF trong ví dụ 5.
Phương pháp giải
Độ dài vectơ →EF là |→EF|=EF
Lời giải
→EE,→MM,→FFcó điểm đầu và điểm cuối trùng nhau nên chúng là vectơ không, có độ dài bằng 0.
|→EE|=|→MM|=|→FF|=0
EF=2,EM=12EF=1⇒|→EF|=2,|→EM|=1
Bài tập
Bài 1 trang 86 Toán 10 Tập 1: a) Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:
- Bác Ba có số tiền 20 triệu đồng
- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc.
b) Trong các đại lượng sau, đại lượng nào cần được biểu diễn bởi vectơ?
Giá tiền, lực, thể tích, tuổi, độ dịch chuyển, vận tốc
Lời giải
a) Sự khác biệt là:
- Đơn vị của 2 đại lượng: triệu đồng và km/h
- 20 triệu đồng là 1 đại lượng vô hướng còn cơn bão là đại lượng có hướng cụ thể là hướng từ đông sang bắc với vận tốc là 20 km/h
b) Các đại lượng cần biểu diễn vectơ là các đại lượng có hướng nên đó là: lực, độ dịch chuyển, vận tốc.
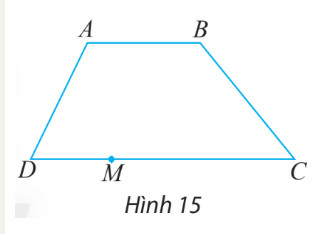
a) Gọi tên các vectơ cùng hướng với vectơ →AB
b) Gọi tên các vectơ ngược hướng với vectơ →DM
Phương pháp giải
a) Bước 1: Từ h15 tìm các cạnh song song hoặc trùng với cạnh AB
Bước 2: Trong đó, chỉ ra các vectơ có hướng từ trái
qua phải.
b) Bước 1: Từ h15 tìm các cạnh song song hoặc trùng với cạnh DM
Bước 2: Trong đó, chỉ ra các vectơ có hướng từ trái qua phải.
Lời giải
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ →AB là các vectơ có hướng từ trái qua phải nên đó là: →DC,→DM,→MC
b) →DMcó hướng từ trái sang phải nên các vectơ ngược hướng với vectơ →DM là →BA,→MD,→CM,→CD
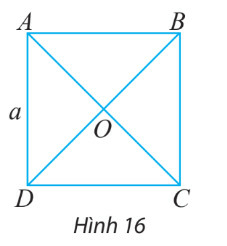
Bài 3 trang 86 Toán 10 Tập 1: Cho hình vuông ABCD có tâm O và có các cạnh bằng a (hình 16)
a) Tìm trong hình hai vectơ bằng nhau và có độ dài bằng a√22
b) Tìm trong hình hai vectơ đối nhau và có độ dài bằng a√2
Phương pháp giải
a) Bước 1: Tìm độ dài các cạnh AB,BC,CD,DA,AC,BD...
Bước 2: Xác định hướng của các vectơ có độ dài bằng a√22
Bước 3: Từ bước 2, chỉ ra hai vectơ cùng hướng
Lời giải
a) AC=BD=√AD2+DC2=√a2+a2=a√2
⇒AO=OC=BO=OD=a√22
Suy ra các cặp vectơ bằng nhau và có độ dài bằng a√22 là:
→AOvà →OC; →CO và →OA; →DO và →OB; →OD và →BO
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là a√2.
Do đó hai vectơ đối nhau và có độ dài bằng a√2 là:
→ACvà →CA; →BD và →DB.
Phương pháp giải
→AB=→DC nếu
+ →AB,→DC cùng hướng
+ AB=CD
Lời giải
Tứ giác ABCD là hình bình hành
⇔{AB//DCAB=DC
Mà AB//DC⇔→AB,→DC cùng phương, do đó cùng hướng.
⇔{→AB,→DCcùnghướngAB=DC
⇔→AB=→DC
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi →AB=→DC.
Phương pháp giải
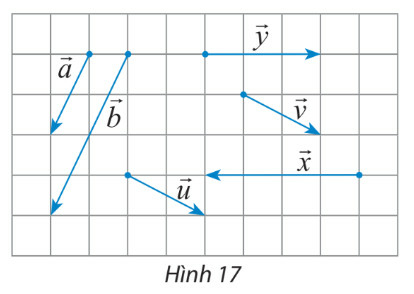
Bước 1: Xác định các vecto có giá song song hoặc trùng nhau
Bước 2: Xác định hướng của các vectơ => Kết luận các cặp vecto cùng hướng, ngược hướng.
Bước 3: So sánh độ dài của các cặp vecto cùng hướng => Kết luận các cặp vecto bằng nhau
Lời giải
+ Các cặp vectơ cùng hướng là: →a và →b; →u và →v
+ Các cặp vectơ ngược hướng là: →x và →y
+ Các cặp vectơ bằng nhau là: →u và →v
Bài 6 trang 87 Toán 10 Tập 1: Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ →0 và cùng hướng với vectơ →OA.
b) Tìm các vectơ bằng vectơ →AB.
Phương pháp giải
a)
Bước 1: Xác định các cạnh song song hoặc trùng với cạnh OA
Bước 2: Chỉ ra các vectơ cùng hướng với vectơ →OA
b)
Bước 1: Xác định các cạnh song song hoặc trùng cạnh AB
Bước 2: Chỉ ra các vectơ có cùng hướng với vectơ →AB
Bước 3: Trong đó, kết luận các vectơ có độ dài bằng cạnh AB
Lời giải
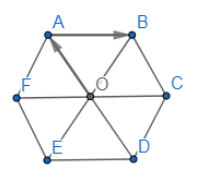
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ →0 và cùng hướng với vectơ →OA là : →DO,→DA,→CB,→EF
b) Ta có: OA=OB=OC=OD=OE=FO và AB // EC // ED
Suy ra các vectơ bằng vectơ →AB là →FO,→OC,→ED
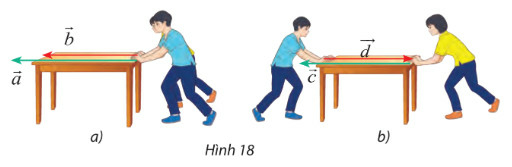
Lời giải
Nhận xét: giá của 4 lực đều song song hoặc trùng nhau, do đó 4 vecto là cùng phương.
Vectơ →a,→b,→c có chiều từ phải sang trái còn vectơ →d có chiều từ trái sang phải
Vậy các vectơ (hay lực) cùng hướng với nhau là vectơ →a,→b,→c.
Các vectơ (lực) →a,→b,→c ngược hướng với vectơ →d.
Lý thuyết Bài 1. Khái niệm vectơ
1. ĐỊNH NGHĨA VECTƠ
+) Vecto là một đoạn thẳng có hướng.
Ví dụ: i) vecto →AB: (đọc là vecto AB)

ii) Vecto →BA:

iii) vecto →u: (khi không chỉ rõ điểm đầu, điểm cuối)
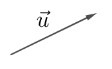
+) Giá của vecto: là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.
Ví dụ: Giá của vecto →CD là đường thẳng CD
+) Độ dài của vecto là →AB là độ dài đoạn thẳng AB.
Kí hiệu: |→AB| và |→AB|=AB.
2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU
+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.
Ví dụ:
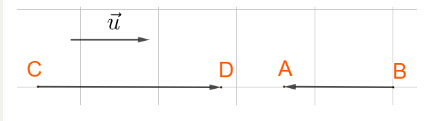
Ba vecto →u,→CD,→AB cùng phương.
Trong đó 2 vecto →u,→CD cùng hướng, còn 2 vecto →CD,→AB ngược hướng.
+) Ba điểm A, B, C thẳng hàng khi và chỉ khi →AB và →AC cùng phương.
3. HAI VECTƠ BẰNG NHAU - VECTƠ ĐỐI NHAU
+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
+) Hai vecto được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng.
Kí hiệu: →a=−→b (vecto →b là vecto đối của vecto →a)
+) Với mỗi điểm O và vecto →a cho trước, có duy nhất điểm A sao cho →OA=→a
4. VECTƠ - KHÔNG
+) Vecto không, là vecto có điểm đầu và điểm cuối trùng nhau. Ví dụ: →AA,→EE,...
Kí hiệu chung là →0.
* Chú ý:
- Vecto không có độ dài bằng 0.
- Vecto →0 cùng phương, cùng hướng với mọi vecto.
- Mọi vecto-không đều bằng nhau: →0=→AA=→BB=...
- Vecto đối của vecto-không là chính nó.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.