SBT Toán 10 Chân trời sáng tạo: Bài tập cuối chương V

Phương Thảo Ngày: 15-02-2023 Lớp 10

485

Với Giải SBT Toán 10 Tập 1 trong Bài tập cuối chương 5 Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

SBT Toán 10 Chân trời sáng tạo: Bài tập cuối chương V

I. TRẮC NGHIỆM

Câu hỏi trang 101 SBT Toán 10

Bài 1 trang 101 SBT Toán 10: Cho hình chữ nhật ABCD có $A B = 3, B C = 4$ . Độ dài của vectơ $\vec{A C}$ là:

A. 5

B. 6

C. 7

D. 9

Lời giải:

Ta có $\vec{A C} = A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{3^{2} + 4^{2}} = 5$

Chọn A

Bài 2 trang 101 SBT Toán 10: Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ $\vec{O C}$ có điểm đầu và điểm cuối la các đỉnh của lục giác là:

A. 2

B. 3

C. 4

D. 6

Lời giải

Các vectơ bằng vectơ $\vec{O C}$ là các vectơ có giá song song với cạnh OC , có cùng hướng với vectơ đó và độ dài của cạnh OC

Vậy các vectơ bằng vectơ $\vec{O C}$ là : $\vec{A B}, \vec{F O}, \vec{E D}$

Suy ra các vectơ bằng vectơ $\vec{O C}$ có điểm đầu và điểm cuối la các đỉnh của lục giác là $\vec{A B}, \vec{E D}$ .

Chọn A. 2

Bài 3 trang 101 SBT Toán 10: Cho ba diểm phân biết A, B, C. Khằng định nào sau đây là đúng?

A. $\vec{C A} - \vec{B A} = \vec{B C}$

B. $\vec{A B} + \vec{A C} = \vec{B C}$

C. $\vec{A B} + \vec{C A} = \vec{C B}$

D. $\vec{A B} - \vec{B C} = \vec{C A}$

Lời giải:

A. $\vec{C A} - \vec{B A} = \vec{C A} + \vec{A B} \vec{C B}$ => Loại A

B sai vì $\vec{B A} + \vec{A C} = \vec{B C}$

C. $\vec{A B} + \vec{C A} = \vec{C A} + \vec{A B} = \vec{C B}$ => C đúng

Chọn C.

Bài 4 trang 101 SBT Toán 10: Cho hai điểm phân biệt A và B. Điều kiện để điểm I là trung điểm của đoạn thẳng AB là:

A. $I A = I B$

B. $\vec{I A} = \vec{I B}$

C. $\vec{I A} = - \vec{I B}$

D. $\vec{A I} = \vec{B I}$

Lời giải:

Để I là trung điểm của đoạn thẳng AB thì I phải nằm giữa A, B và $I A = I B$

$\Leftrightarrow \vec{I A}, \vec{I B}$ đối nhau hay $\vec{I A} = - \vec{I B}$

Chọn C.

Bài 5 trang 101 SBT Toán 10: Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC. Khẳng định nào sau đây là đúng?

A. $\vec{G A} = 2 \vec{G I}$

B. $\vec{I G} = - \frac{1}{3} \vec{I A}$

C. $\vec{G B} + \vec{G C} = 2 \vec{G I}$

D. $\vec{G B} + \vec{G C} = \vec{G A}$

Lời giải:

Áp dụng tính chất trọng tâm ta có: $\vec{G B} + \vec{G C} + \vec{G A} = \vec{0}; \vec{A G} = \frac{2}{3} \vec{A I}$

Chọn C

Câu hỏi trang 102 Toán 10

Bài 6 trang 102 SBT Toán 10: Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?

A. $\vec{A C} + \vec{B D} = 2 \vec{B C}$

B. $\vec{A C} + \vec{B C} = \vec{A B}$

C. $\vec{A C} + \vec{B D} = 2 \vec{C D}$

D. $\vec{A C} + \vec{A D} = \vec{C D}$

Lời giải:

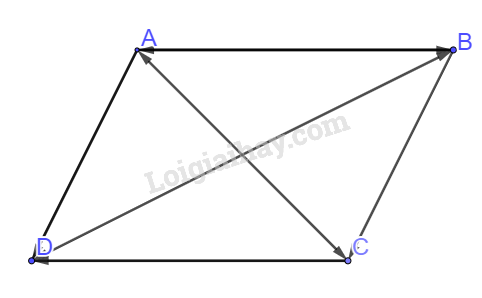
Áp dụng quy tắc và tính chất của hình bình hành ta có

$\vec{A C} + \vec{B D} = (\vec{A B} + \vec{A D}) + (\vec{B A} + \vec{B C}) = \vec{A D} + \vec{B C} = 2 \vec{B C}$

Chọn A

Bài 7 trang 102 SBT Toán 10: Cho tam giác ABC. Đặt $\vec{a} = \vec{A B}; \vec{b} = \vec{A C}$ . Các cặp vectơ nào sau đây cùng phương?

A. $2 \vec{a} + \vec{b}$ và $\vec{a} + 2 \vec{b}$

B. $\vec{a} - 2 \vec{b}$ và $2 \vec{a} - \vec{b}$

C. $5 \vec{a} + \vec{b}$ và $- 10 \vec{a} - 2 \vec{b}$

D. $\vec{a} + \vec{b}$ và $\vec{a} - \vec{b}$

Lời giải:

Ta có:

$- 10 \vec{a} - 2 \vec{b} = - 2 (5 \vec{a} + \vec{b})$

=> Hai vecto $5 \vec{a} + \vec{b}$ và $- 10 \vec{a} - 2 \vec{b}$ cùng phương.

=> Chọn C

Xét các đáp án còn lại:

Giả sử $2 \vec{a} + \vec{b} = k (\vec{a} + 2 \vec{b})$

$\Leftrightarrow (2 - k) \vec{a} = (2 k - 1) \vec{b}$

Mà $\vec{a}, \vec{b} \neq \vec{0}$

=> $\vec{a}, \vec{b}$ cùng phương (Vô lí vì A, B, C không thẳng hàng)

=> Loại A

Tương tự, ta loại các đáp án B, D.

Bài 8 trang 102 SBT Toán 10: Tam giác ABC vuông ở A và có $\hat{B} = 50^{\circ}$ . Khẳng định nào sau đây là sai?

A. $(\vec{A B}, \vec{B C}) = 130^{\circ}$

B. $(\vec{B C}, \vec{A C}) = 40^{\circ}$

C. $(\vec{A B}, \vec{C B}) = 50^{\circ}$

D. $(\vec{A C}, \vec{C B}) = 120^{\circ}$

Lời giải:

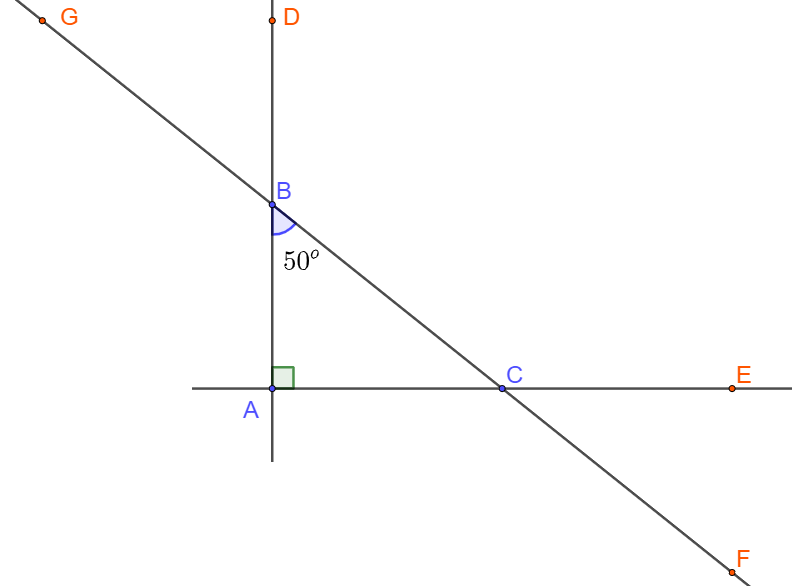
Ta có $\hat{C} = 180^{\circ} - \hat{A} - \hat{B} = 40^{\circ}$

+ $(\vec{A B}, \vec{B C}) = (\vec{B D}, \vec{B C}) = \hat{B C D} = 130^{\circ}$ => A đúng

+ $(\vec{B C}, \vec{A C}) = (\vec{C F}, \vec{C E}) = \hat{E C F} = 40^{\circ}$ => B đúng

+ $(\vec{A B}, \vec{C B}) = (\vec{B D}, \vec{B G}) = \hat{D B G} = 50^{\circ}$ => C đúng

+ $(\vec{A C}, \vec{C B}) = (\vec{C E}, \vec{C B}) = \hat{E C B} = 140^{\circ}$ => D sai

Chọn D.

Bài 9 trang 102 SBT Toán 10: Cho $\vec{a}$ và $\vec{b}$ là hai vectơ cùng hướng và đều khác vectơ $\vec{0}$ . Khẳng định nào sau đây là đúng?

A. $\vec{a} . \vec{b} = | \vec{a} | . | \vec{b} |$

B. $\vec{a} . \vec{b} = 0$

C. $\vec{a} . \vec{b} = - 1$

D. $\vec{a} . \vec{b} = - | \vec{a} | . | \vec{b} |$

Lời giải:

Ta có hai vectơ $\vec{a}$ và $\vec{b}$ nên $(\vec{a}, \vec{b}) = 0^{\circ} \Rightarrow \vec{a} . \vec{b} = | \vec{a} | . | \vec{b} | . \cos (\vec{a}, \vec{b}) = | \vec{a} | . | \vec{b} | . \cos 0^{\circ} = | \vec{a} | . | \vec{b} |$

Chọn A.

Bài 10 trang 102 SBT Toán 10: Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai?

A. $\vec{A B} . \vec{A C} < \vec{B A} . \vec{B C}$

B. $\vec{A C} . \vec{C B} < \vec{A C} . \vec{B C}$

C. $\vec{A B} . \vec{B C} < \vec{C A} . \vec{C B}$

D. $\vec{A C} . \vec{B C} < \vec{B C} . \vec{A B}$

Lời giải:

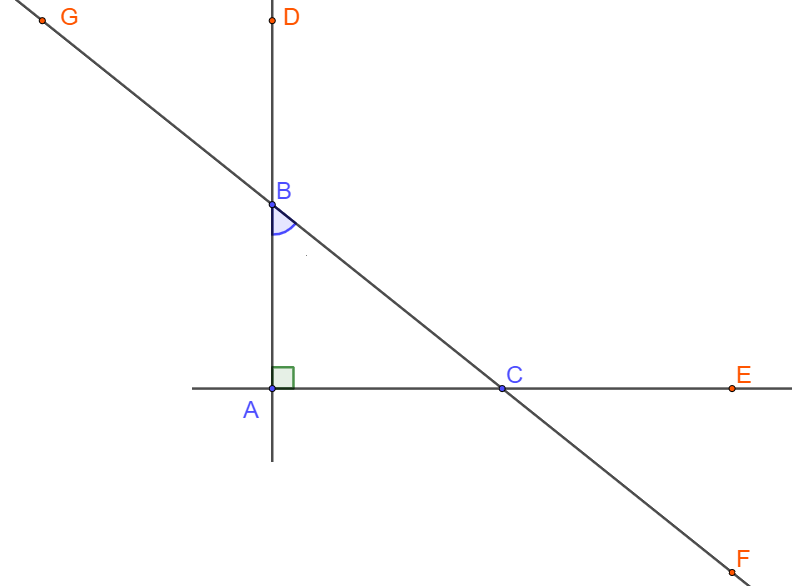
A. $\vec{A B} . \vec{A C} < \vec{B A} . \vec{B C}$

+ $\vec{A B} . \vec{A C} = 0$

+ $\cos (\vec{B A}, \vec{B C}) = \cos B > 0$ (vì $0^{\circ} < \hat{B} < 90^{\circ}$ )

$\Rightarrow \vec{B A} . \vec{B C} > 0 = \vec{A B} . \vec{A C}$ => A đúng

B. $\vec{A C} . \vec{C B} < \vec{A C} . \vec{B C}$

+ $\cos (\vec{A C}, \vec{C B}) = \cos (\vec{C E}, \vec{C B}) = \cos \hat{B C E} < 0$ (vì $\hat{B C E} > 90^{\circ}$ )

+ $\cos (\vec{A C}, \vec{B C}) = \cos (\vec{C E}, \vec{C F}) = \cos \hat{E C F} > 0$ (vì $0^{\circ} < \hat{C} < 90^{\circ}$ )

$\Rightarrow \vec{A C} . \vec{C B} < 0 < \vec{A C} . \vec{B C}$ => B đúng

C. $\vec{A B} . \vec{B C} < \vec{C A} . \vec{C B}$

+ $\cos (\vec{A B}, \vec{B C}) = \cos (\vec{B D}, \vec{B C}) = \cos \hat{C B D} < 0$ (vì $\hat{C B D} > 90^{\circ}$ )

+ $\cos (\vec{C A}, \vec{C B}) = \cos \hat{C} > 0$ (vì $0^{\circ} < \hat{C} < 90^{\circ}$ )

$\Rightarrow \vec{A B} . \vec{B C} < 0 < \vec{C A} . \vec{C B}$ => C đúng

D. $\vec{A C} . \vec{B C} < \vec{B C} . \vec{A B}$

+ $\cos (\vec{A C}, \vec{B C}) = \cos (\vec{C E}, \vec{C F}) = \cos \hat{E C F} > 0$ (vì $0^{\circ} < \hat{E C F} < 90^{\circ}$ )

+ $\cos (\vec{B C}, \vec{A B}) = \cos (\vec{B C}, \vec{B D}) = \cos \hat{C B D} < 0$ (vì $\hat{C B D} > 90^{\circ}$ )

$\Rightarrow \vec{A C} . \vec{B C} > 0 > \vec{B C} . \vec{A B}$ => D đúng

Chọn D.

II. TỰ LUẬN

Bài 1 trang 102 SBT Toán 10: Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ $\vec{A B}$ và $\vec{A C}$ :

a) cùng hướng? b) ngược hướng?

Lời giải:

a) Hai vectơ $\vec{A B}$ và $\vec{A C}$ cùng hướng

=> A, B, C thẳng hàng và B, C nằm về cùng phía so với điểm A.

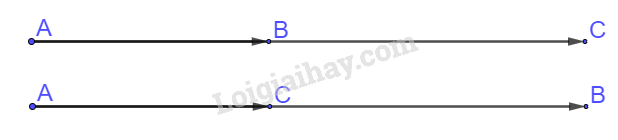
b) Hai vectơ $\vec{A B}$ và $\vec{A C}$ ngược hướng

=> A, B, C thẳng hàng và B, C nằm về hai phía so với điểm A.

(Hay A, B, C thẳng hàng và A nằm giữa B và C)

Bài 2 trang 102 SBT Toán 10: Cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ cùng phương. Chứng tỏ rằng có ít nhất hai vectơ cùng hướng trong ba vectơ đó.

Lời giải:

Hai vecto cùng phương thì cùng hướng hoặc ngược hướng.

+ TH1: $\vec{a}, \vec{b}$ cùng hướng hoặc $\vec{b}, \vec{c}$ cùng hướng

Ta có ngay điều phải chứng minh

+ TH1: $\vec{a}, \vec{b}$ ngược hướng và $\vec{b}, \vec{c}$ ngược hướng

=> $\vec{a}, \vec{c}$ cùng hướng (do cùng ngược hướng với $\vec{b}$ )

Vậy luôn có 2 trong 3 vecto cùng hướng với nhau (đpcm).

Bài 3 trang 102 SBT Toán 10: Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O . Hãy so sánh các vectơ $\vec{A H}$ và $\vec{B^{'} C}, \vec{A B^{'}}$ và $\vec{H C}$

Lời giải:

Ta có B’ là điểm đối xứng với B qua tâm O nên BB’ là đường kính, suy ra $\hat{B^{'} C B} = 90^{\circ} \Rightarrow B^{'} C ⊥ B C$ và $\hat{B^{'} A B} = 90^{\circ} \Rightarrow B^{'} A ⊥ B A$

Mặt khác ta có: $A H ⊥ B C, C H ⊥ A B$ , suy ra $B^{'} C / / A H, A B^{'} / / C H$

Suy ra AB’CH là hình bình hành

Vậy $\vec{A H} = \vec{B^{'} C}$ và $\vec{A B^{'}} = \vec{H C}$

Câu hỏi trang 103 SBT Toán 10

Bài 4 trang 103 SBT Toán 10: Chứng minh rằng với hai vectơ không cùng phương $\vec{a}$ và $\vec{b}$ , ta có:

$| \vec{a} | - | \vec{b} | \leq | \vec{a} + \vec{b} | \leq | \vec{a} | + | \vec{b} |$

Lời giải:

TH1: $\vec{a} = \vec{0}$

$\Rightarrow | \vec{a} | - | \vec{b} | = | \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} | = | \vec{b} |$

TH2: $\vec{b} = \vec{0}$

$\Rightarrow | \vec{a} | - | \vec{b} | = | \vec{a} + \vec{b} | = | \vec{a} | + | \vec{b} | = | \vec{a} |$

TH3: $\vec{a} \neq \vec{0}$ và $\vec{b} \neq \vec{0}$

Lấy A bất kì, vẽ $\vec{A B} = \vec{a}, \vec{A D} = \vec{b}$ . Dựng hình bình hành ABCD, đặt $\vec{c} = \vec{A C}$

Ta có: $\vec{a} + \vec{b} = \vec{A B} + \vec{A D} = \vec{A C} = \vec{c}$

Xét tam giác ABC, theo bất đẳng thức tam giác ta có:

$A B - B C < A C < A B + B C$

Mà $| \vec{a} | = | \vec{A B} | = A B; | \vec{b} | = | \vec{A D} | = A D = B C; | \vec{c} | = | \vec{A C} | = A C;$

$\Rightarrow | \vec{a} | - | \vec{b} | < | \vec{a} + \vec{b} | < | \vec{a} | + | \vec{b} |$

Vậy $| \vec{a} | - | \vec{b} | \leq | \vec{a} + \vec{b} | \leq | \vec{a} | + | \vec{b} |$

Bài 5 trang 103 SBT Toán 10: Cho hình ngũ giác đều ABCDE có tâm O. Chứng minh rằng: $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} + \vec{O E} = \vec{0}$

Lời giải:

Không mất tính tổng quát giả sử $O A = O B = O C = O D = O E = 1$

Ta có: $\hat{A O B} = \hat{B O C} = \hat{C O D} = \hat{D O E} = \hat{E O A} = 360^{\circ} : 5 = 72^{\circ}$

+ Dựng hình bình hành OEHB.

Vì OE=OB nên OEHB là hình thoi, suy ra H thuộc tia phân giác của $\hat{E O B}$ hay H thuộc OA.

$\Rightarrow \vec{O A} + (\vec{O B} + \vec{O E}) = \vec{O A} + \vec{O H} = \vec{O M}$ với M thuộc OA sao cho OM = OH +OA.

+ Tính OM:

Xét tam giác OHE, ta có:

$\hat{H O E} = 72; O E = H E = 1$ $\Rightarrow \hat{O H E} = 72^{o} \Rightarrow \hat{O E H} = 180^{\circ} - 72^{o} - 72^{o} = 36^{\circ}$

Áp dụng định lí cosin: $O H^{2} = O E^{2} + E H^{2} - 2. O E . O H . \cos E$

$\begin{array}{l} \Leftrightarrow O H^{2} = 1 + 1 - 2. \cos 36^{\circ} \approx 0, 382 \\ \Rightarrow O H = 0, 618 \\ \Rightarrow O M = O H + O A = 0, 618 + 1 = 1, 618 \end{array}$

+ Dựng hình bình hành OCKD, ta có: $\vec{O C} + \vec{O D} = \vec{O K}$

Vì OC=OD nên OCKD là hình thoi => OK là tia phân giác của $\hat{C O D}$

$\Rightarrow \hat{C O K} = \frac{1}{2} \hat{C O D} = \frac{1}{2} {.72}^{o} = 36^{o}$

$\Rightarrow \hat{K O A} = \hat{K O C} + \hat{C O B} + \hat{B O A} = 36^{\circ} + 72^{\circ} + 72^{\circ} = 180^{\circ}$

Hay K, O, A thẳng hàng, do đó K, O, M thẳng hàng (do M thuộc OA).

+Tính OK:

Xét tam giác OCK, ta có:

$\begin{array}{l} O C = C K = 1; \hat{C O K} = 36^{o} \Rightarrow \hat{C K O} = 36^{o} \\ \Rightarrow \hat{O C K} = 180^{o} - 36^{o} - 36^{o} = 108^{o} \\ \Rightarrow O K^{2} = O C^{2} + C K^{2} - 2. O C . C K . \cos \hat{O C K} \\ \Leftrightarrow O K^{2} = 1 + 1 - 2. \cos 108^{o} \approx 2, 618 \\ \Rightarrow O K = 1, 618 = O M \end{array}$

Vậy O là trung điểm KM hay $\vec{O K} + \vec{O M} = \vec{0}$

$\begin{array}{l} \Rightarrow \vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} + \vec{O E} = (\vec{O A} + \vec{O B} + \vec{O E}) + (\vec{O C} + \vec{O D}) \\ = \vec{O M} + \vec{O K} = \vec{0} (d p c m) \end{array}$