Với giải Câu hỏi trang 102 SBT Toán 10 Tập 1 Chân trời sáng tạo trong Bài tập cuối chương 5 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:
Nội dung bài viết
SBT Toán 10 Chân trời sáng tạo trang 102: Bài tập cuối chương 5
Bài 6 trang 102 SBT Toán 10: Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng?
A. →AC+→BD=2→BC
B. →AC+→BC=→AB
C. →AC+→BD=2→CD
D. →AC+→AD=→CD
Lời giải:
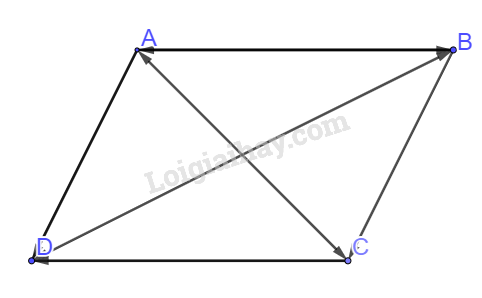
Áp dụng quy tắc và tính chất của hình bình hành ta có
→AC+→BD=(→AB+→AD)+(→BA+→BC)=→AD+→BC=2→BC
Chọn A
Bài 7 trang 102 SBT Toán 10: Cho tam giác ABC. Đặt →a=→AB;→b=→AC. Các cặp vectơ nào sau đây cùng phương?
A. 2→a+→b và →a+2→b
B. →a−2→b và 2→a−→b
C. 5→a+→b và −10→a−2→b
D. →a+→b và →a−→b
Lời giải:
Ta có:
−10→a−2→b=−2(5→a+→b)
=> Hai vecto 5→a+→b và −10→a−2→b cùng phương.
=> Chọn C
Xét các đáp án còn lại:
Giả sử 2→a+→b=k(→a+2→b)
⇔(2−k)→a=(2k−1)→b
Mà →a,→b≠→0
=> →a,→b cùng phương (Vô lí vì A, B, C không thẳng hàng)
=> Loại A
Tương tự, ta loại các đáp án B, D.
Bài 8 trang 102 SBT Toán 10: Tam giác ABC vuông ở A và có ˆB=50∘. Khẳng định nào sau đây là sai?
A. (→AB,→BC)=130∘
B. (→BC,→AC)=40∘
C. (→AB,→CB)=50∘
D. (→AC,→CB)=120∘
Lời giải:
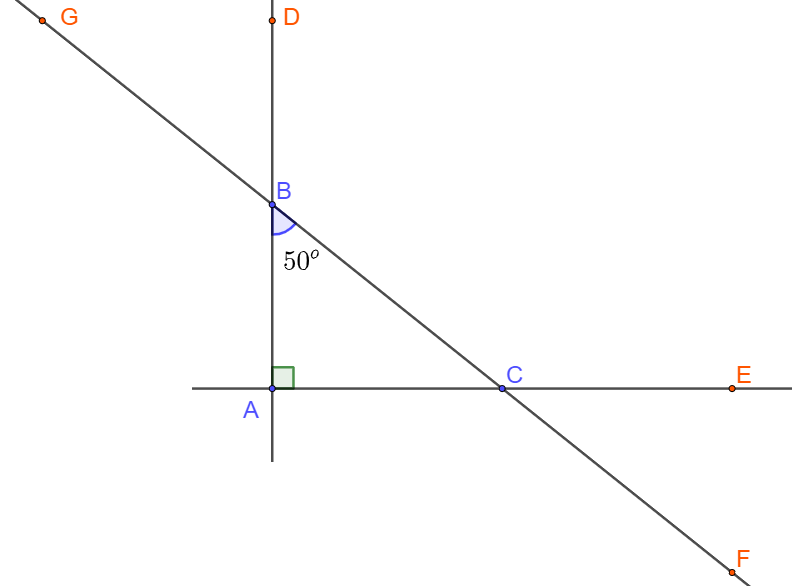
Ta có ˆC=180∘−ˆA−ˆB=40∘
+ (→AB,→BC)=(→BD,→BC)=^BCD=130∘ => A đúng
+ (→BC,→AC)=(→CF,→CE)=^ECF=40∘ => B đúng
+ (→AB,→CB)=(→BD,→BG)=^DBG=50∘ => C đúng
+ (→AC,→CB)=(→CE,→CB)=^ECB=140∘ => D sai
Chọn D.
Bài 9 trang 102 SBT Toán 10: Cho →a và →b là hai vectơ cùng hướng và đều khác vectơ →0. Khẳng định nào sau đây là đúng?
A. →a.→b=|→a|.|→b|
B. →a.→b=0
C. →a.→b=−1
D. →a.→b=−|→a|.|→b|
Lời giải:
Ta có hai vectơ →a và →b nên(→a,→b)=0∘⇒→a.→b=|→a|.|→b|.cos(→a,→b)=|→a|.|→b|.cos0∘=|→a|.|→b|
Chọn A.
Bài 10 trang 102 SBT Toán 10: Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai?
A. →AB.→AC<→BA.→BC
B. →AC.→CB<→AC.→BC
C. →AB.→BC<→CA.→CB
D. →AC.→BC<→BC.→AB
Lời giải:
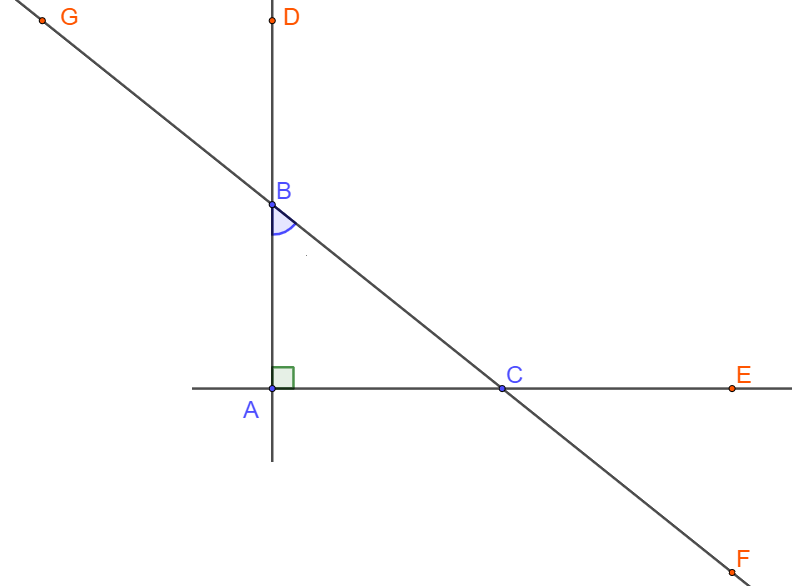
A. →AB.→AC<→BA.→BC
+ →AB.→AC=0
+ cos(→BA,→BC)=cosB>0 (vì 0∘<ˆB<90∘)
⇒→BA.→BC>0=→AB.→AC=> A đúng
B. →AC.→CB<→AC.→BC
+ cos(→AC,→CB)=cos(→CE,→CB)=cos^BCE<0 (vì ^BCE>90∘)
+ cos(→AC,→BC)=cos(→CE,→CF)=cos^ECF>0 (vì 0∘<ˆC<90∘)
⇒→AC.→CB<0<→AC.→BC => B đúng
C. →AB.→BC<→CA.→CB
+ cos(→AB,→BC)=cos(→BD,→BC)=cos^CBD<0 (vì ^CBD>90∘)
+ cos(→CA,→CB)=cosˆC>0 (vì 0∘<ˆC<90∘)
⇒→AB.→BC<0<→CA.→CB => C đúng
D. →AC.→BC<→BC.→AB
+ cos(→AC,→BC)=cos(→CE,→CF)=cos^ECF>0 (vì 0∘<^ECF<90∘)
+ cos(→BC,→AB)=cos(→BC,→BD)=cos^CBD<0 (vì ^CBD>90∘)
⇒→AC.→BC>0>→BC.→AB => D đúng
Chọn D.
II. TỰ LUẬN
Bài 1 trang 102 SBT Toán 10: Cho ba điểm A, B, C phân biệt thẳng hàng. Trong trường hợp nào thì hai vectơ →AB và →AC:
a) cùng hướng? b) ngược hướng?
Lời giải:
a) Hai vectơ →AB và →AC cùng hướng
=> A, B, C thẳng hàng và B, C nằm về cùng phía so với điểm A.
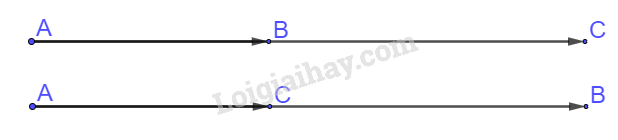
b) Hai vectơ →AB và →AC ngược hướng
=> A, B, C thẳng hàng và B, C nằm về hai phía so với điểm A.
(Hay A, B, C thẳng hàng và A nằm giữa B và C)
Bài 2 trang 102 SBT Toán 10: Cho ba vectơ →a,→b,→c cùng phương. Chứng tỏ rằng có ít nhất hai vectơ cùng hướng trong ba vectơ đó.
Lời giải:
Hai vecto cùng phương thì cùng hướng hoặc ngược hướng.
+ TH1: →a,→b cùng hướng hoặc →b,→c cùng hướng
Ta có ngay điều phải chứng minh
+ TH1: →a,→b ngược hướng và →b,→c ngược hướng
=> →a,→c cùng hướng (do cùng ngược hướng với →b)
Vậy luôn có 2 trong 3 vecto cùng hướng với nhau (đpcm).
Bài 3 trang 102 SBT Toán 10: Cho tam giác ABC nội tiếp trong đường tròn (O). Gọi H là trực tâm tam giác ABC và B’ là điểm đối xứng với B qua tâm O . Hãy so sánh các vectơ →AH và →B′C,→AB′ và →HC
Lời giải:

Ta có B’ là điểm đối xứng với B qua tâm O nên BB’ là đường kính, suy ra ^B′CB=90∘⇒B′C⊥BC và ^B′AB=90∘⇒B′A⊥BA
Mặt khác ta có: AH⊥BC,CH⊥AB, suy ra B′C//AH,AB′//CH
Suy ra AB’CH là hình bình hành
Vậy →AH=→B′C và →AB′=→HC
Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 101 SBT Toán 10: Cho hình chữ nhật ABCD có Ab = 3, BC = 4. Độ dài của vecto AC là....
Bài 2 trang 101 SBT Toán 10: Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ...
Bài 3 trang 101 SBT Toán 10: Cho ba diểm phân biết A, B, C. Khằng định nào sau đây là đúng?....
Nội dung bài viết
Bài 5 trang 101 SBT Toán 10: Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC...
Bài 6 trang 102 SBT Toán 10: Cho hình bình hành ABCD. Khẳng định nào sau đây là đúng....
Bài 7 trang 102 SBT Toán 10: Cho tam giác ABC.....
Bài 8 trang 102 SBT Toán 10: Tam giác ABC vuông ở A và có ...
Bài 10 trang 102 SBT Toán 10: Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là sai...
Bài 1 trang 102 SBT Toán 10: Cho ba điểm A, B, C phân biệt thẳng hàng...
Bài 2 trang 102 SBT Toán 10: Cho ba vectơ →a,→b,→c cùng phươngChứng tỏ có ít nhất hai vecto cùng hường trong3 vecto đó...p trong đường tròn (O)....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.