Với giải Câu hỏi trang 28 Toán 10 Tập 1 Kết nối tri thức trong Bài 4: Hệ bất phương trình bậc nhất hai ẩn học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức trang 28 Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Luyện tập 2 trang 28 Toán lớp 10: Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:
Phương pháp giải:
Bước 1: Xác định miền nghiệm của bất phương trình
Bước 2: Xác định miền nghiệm của bất phương trình
Bước 3: Xác định miền nghiệm của bất phương trình
Bước 4: Xác định miền nghiệm của bất phương trình
Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
Lời giải:
Bước 1: Xác định miền nghiệm của bất phương trình
Miền nghiệm của bất phương trình là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Bước 2: Xác định miền nghiệm của bất phương trình
Miền nghiệm của bất phương trình là nửa mặt phẳng bờ Ox chứa điểm (0;1) không kể trục Ox.
Bước 3: Xác định miền nghiệm của bất phương trình
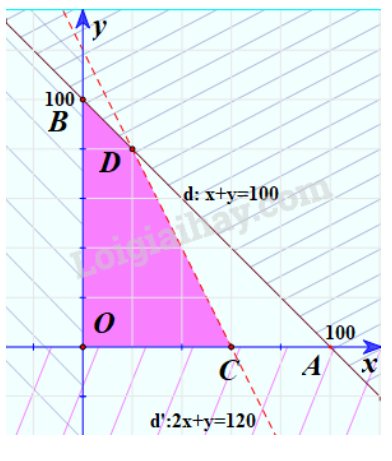
+ Vẽ đường thẳng d: x+y=100
+ Vì 0+0=0
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Bước 4: Xác định miền nghiệm của bất phương trình
Tương tự miền nghiệm của bất phương trình là nửa mặt phẳng bờ d’ chúa gốc tọa độ O. (không kể đường thẳng d’).
Khi đó miền không bị gạch là giao của các miền nghiệm của các bất phương trình trong hệ. Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không kể đoạn thẳng OC và CD).
3. ỨNG DỤNG CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Hoạt động 3 trang 28 Toán lớp 10: Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5).
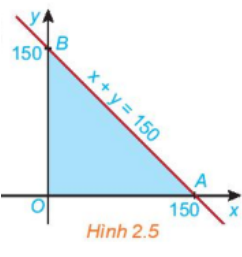
a) Tính giá trị của biểu thức F(x; y) tại mỗi đỉnh O, A và B.
b) Nêu nhận xét về dấu của hoành độ x và tung độ y của điểm (x; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị nhỏ nhất của F(x; y) trên miền tam giác OAB.
c) Nêu nhận xét về tổng x + y của điểm (X; y) nằm trong miền tam giác OAB. Từ đó suy ra giá trị lớn nhất của F(x, y) trên miền tam giác OAB.
Phương pháp giải:
a) Thay tọa độ điểm O, A, B vào F(x;y) và tính giá trị.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Xác định dấu:
+ So sánh x với 0
+ So sánh y với 0
Đánh giá biểu thức F(x;y) dựa vào dấu của x và y, từ đó tìm giá trị nhỏ nhất của biểu thức.
c) Dựa vào biểu thức
Giá trị lớn nhất: Tách 2x+3y =2.(x+y)+y và dựa vào việc đánh giá x+y và y ở bước trên để tìm giá trị lớn nhất.
Lời giải:
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình nên mọi điểm (x;y) thuộc miền OAB thỏa mãn .
Vì miền OAB là miền nghiệm của hệ bất phương trình nên mọi điểm (x;y) thuộc miền OAB thỏa mãn .
Vậy và .
=>
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình nên mọi điểm (x;y) thuộc miền OAB thỏa mãn
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có .
Vậy ta có:
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.
Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:
Hoạt động 1 trang 26 Toán 10: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hoà loại hai chiều và một chiều mà cửa hàng cần nhập...
Luyện tập 2 trang 28 Toán 10: Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ:...
Hoạt động 3 trang 28 Toán 10: Xét biểu thức F(x, y) = 2x + 3y với (x; y) thuộc miền tam giác OAB ở HĐ2. Toạ độ ba đình là O(0, 0), A(150, 0) và B(0; 150) (H.2.5)...
Câu hỏi vận dụng trang 30 Toán 10: Một cửa hàng có kế hoạch nhập về hai loại máy tính A và B, giá mỗi chiếc lần lượt là 10 triệu đồng và 20 triệu đồng với số vốn ban đầu không vượt quá 4 tỉ đồng...
Bài 2.4 trang 30 Toán 10: Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Bài 2.6 trang 30 Toán 10: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.