Toán 10 Kết nối tri thức trang 44: Bài tập cuối chương 3

Giang Ngày: 12-02-2023 Lớp 10

145

Với giải Câu hỏi trang 44 Toán 10 Tập 1 Kết nối tri thức trong Bài tập cuối chương 3 học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Kết nối tri thức trang 44: Bài tập cuối chương 3

Bài 3.12 trang 44 Toán lớp 10: Cho tam giác ABC có $\hat{B} = 135^{o}$ . Khẳng định nào sau đây là đúng?

Lời giải a

A. $S = \frac{1}{2} c a$

B. $S = \frac{- \sqrt{2}}{4} a c$

C. $S = \frac{\sqrt{2}}{4} b c$

D. $S = \frac{\sqrt{2}}{4} c a$

Phương pháp giải:

Diện tích tam giác ABC: $S = \frac{1}{2} a c . \sin B$

Lời giải:

Diện tích tam giác ABC: $S = \frac{1}{2} a c . \sin B$

Mà $\hat{B} = 135^{o} \Rightarrow \sin B = \sin 135^{o} = \frac{\sqrt{2}}{2}$ .

$\Rightarrow S = \frac{1}{2} a c . \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{4} . a c$

Chọn D

Lời giải b

A. $R = \frac{a}{\sin A}$

B. $R = \frac{\sqrt{2}}{2} b$

C. $R = \frac{\sqrt{2}}{2} c$

D. $R = \frac{\sqrt{2}}{2} a$

Phương pháp giải:

Định lí sin: $R = \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Lời giải:

Theo định lí sin, ta có: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = R$

A. $R = \frac{a}{\sin A}$ đúng

B. $R = \frac{\sqrt{2}}{2} b$

Mà $\sin B = \frac{\sqrt{2}}{2} \Rightarrow R = \frac{b}{\sin B} = \frac{b}{\frac{\sqrt{2}}{2}} = b \sqrt{2}$

Vậy B sai.

C. $R = \frac{\sqrt{2}}{2} c$ (Loại vì không có dữ kiện về góc C nên không thể tính R theo c.)

D. $R = \frac{\sqrt{2}}{2} a$ (Loại vì không có dữ kiện về góc A nên không thể tính R theo a.)

Chọn A

Lời giải c

A. $a^{2} = b^{2} + c^{2} + \sqrt{2} a b .$

B. $\frac{b}{\sin A} = \frac{a}{\sin B}$

C. $\sin B = \frac{- \sqrt{2}}{2}$

D. $b^{2} = c^{2} + a^{2} - 2 c a \cos 135^{o} .$

Phương pháp giải:

Định lí sin: $R = \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Định lí cos: $b^{2} = c^{2} + a^{2} - 2 c a . \cos B; a^{2} = c^{2} + b^{2} - 2 b c . \cos A$

Lời giải:

A. $a^{2} = b^{2} + c^{2} + \sqrt{2} a b .$ (Loại)

Vì: Theo định lí cos ta có: $a^{2} = b^{2} + c^{2} - 2 b c . \cos A$

Không đủ dữ kiện để suy ra $a^{2} = b^{2} + c^{2} + \sqrt{2} a b .$

B. $\frac{b}{\sin A} = \frac{a}{\sin B}$ (Loại)

Theo định lí sin, ta có: $\frac{a}{\sin A} = \frac{b}{\sin B} ⇏ \frac{b}{\sin A} = \frac{a}{\sin B}$

C. $\sin B = \frac{- \sqrt{2}}{2}$ (sai vì theo câu a, $\sin B = \frac{\sqrt{2}}{2}$ )

D. $b^{2} = c^{2} + a^{2} - 2 c a \cos 135^{o} .$

Theo định lý cos ta có:

$b^{2} = c^{2} + a^{2} - 2 c a . \cos B$ (*)

Mà $\hat{B} = 135^{o} \Rightarrow \cos B = \cos 135^{o}$ .

Thay vào (*) ta được: $b^{2} = c^{2} + a^{2} - 2 c a \cos 135^{o}$

=> D đúng.

Chọn D

Bài 3.13 trang 44 Toán lớp 10: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

Lời giải a

A. $S = \frac{a b c}{4 r}$

B. $r = \frac{2 S}{a + b + c}$

C. $a^{2} = b^{2} + c^{2} + 2 b c \cos A$

D. $S = r (a + b + c)$

Phương pháp giải:

+) Định lí cos: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

+) Công thức tính diện tích: $S = p r = \frac{a b c}{4 R}$

Lời giải:

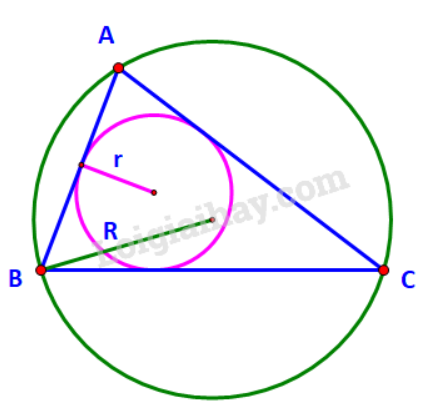
Bài 3.13 trang 44 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

a) Chọn đáp án B

A. $S = \frac{a b c}{4 r}$

Ta có: $S = \frac{a b c}{4 R}$ . Mà $r < R$ nên suy ra $S = \frac{a b c}{4 R} < \frac{a b c}{4 r}$

Vậy A sai.

B. $r = \frac{2 S}{a + b + c}$

Ta có: $S = p r \Rightarrow r = \frac{S}{p}$

Mà $p = \frac{a + b + c}{2} \Rightarrow r = \frac{S}{p} = \frac{S}{\frac{a + b + c}{2}} = \frac{2 S}{a + b + c}$

Vậy B đúng

C. $a^{2} = b^{2} + c^{2} + 2 b c \cos A$

Sai vì theo định lí cos ta có: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$

D. $S = r (a + b + c)$

Sai vì $S = p r = r . \frac{a + b + c}{2}$

b) Chọn đáp án A

A. $\sin A = \sin (B + C)$

Ta có: $\hat{A} + \hat{B} + \hat{C} = 180^{o}$

$\begin{array}{l} \Rightarrow \hat{B} + \hat{C} = 180^{o} - \hat{A} \\ \Rightarrow \sin (B + C) = \sin A \end{array}$

Vậy A đúng.

B. $\cos A = \cos (B + C)$

Sai vì $\cos (B + C) = - \cos A$ (Do $\hat{A} + \hat{B} + \hat{C} = 180^{o}$ )

C. $\cos A > 0$

Không đủ dữ kiện để kết luận.

Nếu $0^{o} < \hat{A} < 90^{o}$ thì $\cos A > 0$

Nếu $90^{o} < \hat{A} < 180^{o}$ thì $\cos A < 0$

D. $\sin A \leq 0$

Ta có $S = \frac{1}{2} b c . \sin A > 0$

Mà $b, c > 0$

$\Rightarrow \sin A > 0$

Vậy D sai.

Lời giải b

A. $\sin A = \sin (B + C)$

B. $\cos A = \cos (B + C)$

C. $\cos A > 0$

D. $\sin A \leq 0$

Phương pháp giải:

Giá trị lượng giác của hai góc bù nhau:

$\sin x = \sin (180^{o} - x)$ ; $- \cos x = \cos (180^{o} - x)$

Lời giải:

A. $\sin A = \sin (B + C)$

Ta có: $(\hat{A} + \hat{C}) + \hat{B} = 180^{o}$

$\Rightarrow \sin (B + C) = \sin A$

=> A đúng.

B. $\cos A = \cos (B + C)$

Sai vì $\cos (B + C) = - \cos A$

C. $\cos A > 0$ Không đủ dữ kiện để kết luận.

Nếu $0^{o} < \hat{A} < 90^{o}$ thì $\cos A > 0$

Nếu $90^{o} < \hat{A} < 180^{o}$ thì $\cos A < 0$

D. $\sin A \leq 0$

Ta có $S = \frac{1}{2} b c . \sin A > 0$ . Mà $b, c > 0$

$\Rightarrow \sin A > 0$

=> D sai.

Chọn A

B. TỰ LUẬN

Bài 3.14 trang 44 Toán lớp 10: Tính giá trị của các biểu thức sau:

a) $M = \sin 45^{o} . \cos 45^{o} + \sin 30^{o}$

b) $N = \sin 60^{o} . \cos 30^{o} + \frac{1}{2} . \sin 45^{o} . \cos 45^{o}$

c) $P = 1 + \tan^{2} 60^{o}$

d) $Q = \frac{1}{\sin^{2} 120^{o}} - \cot^{2} 120^{o} .$

Phương pháp giải:

Bảng giá trị lượng giác của các góc đặc biệt

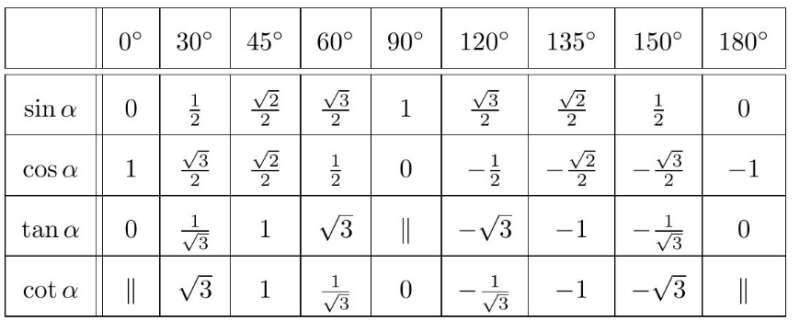
Bài 3.14 trang 44 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

Lời giải:

a) $M = \sin 45^{o} . \cos 45^{o} + \sin 30^{o}$

Ta có: ${\begin{cases} \sin 45^{o} = \cos 45^{o} = \frac{\sqrt{2}}{2}; \\ \sin 30^{o} = \frac{1}{2} \end{cases}$

Thay vào M, ta được: $M = \frac{\sqrt{2}}{2} . \frac{\sqrt{2}}{2} + \frac{1}{2} = \frac{2}{4} + \frac{1}{2} = 1$

b) $N = \sin 60^{o} . \cos 30^{o} + \frac{1}{2} . \sin 45^{o} . \cos 45^{o}$

Ta có: $\sin 60^{o} = \frac{\sqrt{3}}{2}; \cos 30^{o} = \frac{\sqrt{3}}{2}; \sin 45^{o} = \frac{\sqrt{2}}{2}; \cos 45^{o} = \frac{\sqrt{2}}{2}$

Thay vào N, ta được: $N = \frac{\sqrt{3}}{2} . \frac{\sqrt{3}}{2} + \frac{1}{2} . \frac{\sqrt{2}}{2} . \frac{\sqrt{2}}{2} = \frac{3}{4} + \frac{1}{4} = 1$

c) $P = 1 + \tan^{2} 60^{o}$

Ta có: $\tan 60^{o} = \sqrt{3}$

Thay vào P, ta được: $Q = 1 + {(\sqrt{3})}^{2} = 4.$

d) $Q = \frac{1}{\sin^{2} 120^{o}} - \cot^{2} 120^{o} .$

Ta có: $\sin 120^{o} = \frac{\sqrt{3}}{2}; \cot 120^{o} = \frac{- 1}{\sqrt{3}}$

Thay vào P, ta được: $Q = \frac{1}{{(\frac{\sqrt{3}}{2})}^{2}} - {(\frac{- 1}{\sqrt{3}})}^{2} = \frac{1}{\frac{3}{4}} - \frac{1}{3} = \frac{4}{3} - \frac{1}{3} = 1.$

Bài 3.15 trang 44 Toán lớp 10: Cho tam giác ABC có $\hat{B} = 60^{o}, \hat{C} = 45^{o}, A C = 10$ . Tính $a, R, S, r$ .

Phương pháp giải:

Định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = R$

Lời giải:

Theo định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = R$

+) Ta có: $R = \frac{b}{\sin B}$

Mà $b = A C = 10, \hat{B} = 60^{o}$

$\Rightarrow R = \frac{10}{\sin 60^{o}} = \frac{10}{\frac{\sqrt{3}}{2}} = \frac{20}{\sqrt{3}} = \frac{20 \sqrt{3}}{3} .$

+) Mặt khác: $R = \frac{a}{\sin A} \Rightarrow a = R . \sin A$

Mà $R = \frac{20 \sqrt{3}}{3}, \hat{A} = 180^{o} - (\hat{B} + \hat{C}) = 180^{o} - (60^{o} + 45^{o}) = 75^{o}$

$\Rightarrow a = \frac{20 \sqrt{3}}{3} . \sin 75^{o} \approx 11, 154$

+) Diện tích tam giác ABC là: $S = \frac{1}{2} a b . \sin \hat{C}$ $\approx \frac{1}{2} .11, 154.10. \sin 60^{o}$ $\approx 48, 3$

+) Lại có: $R = \frac{c}{\sin C}$

$\Rightarrow c = \frac{20 \sqrt{3}}{3} . \sin 45^{o} = \frac{10 \sqrt{6}}{3} \approx 8, 165$

$\Rightarrow p = \frac{a + b + c}{2} \approx \frac{11, 154 + 10 + 8, 165}{2} \approx 14, 66$

$\Rightarrow r = \frac{S}{p} \approx \frac{48, 3}{14, 66} \approx 3, 3$

Bài 3.16 trang 44 Toán lớp 10: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a) $\cos \hat{A M B} + \cos \hat{A M C} = 0$

b) $M A^{2} + M B^{2} - A B^{2} = 2. M A . M B . \cos \hat{A M B}$ và $M A^{2} + M C^{2} - A C^{2} = 2. M A . M C . \cos \hat{A M C}$

c) $M A^{2} = \frac{2 (A B^{2} + A C^{2}) - B C^{2}}{4}$ (công thức đường trung tuyến).

Phương pháp giải:

a) Giá trị lượng giác của hai góc bù nhau:

$- \cos x = \cos (180^{o} - x)$

b) Định lí cos: $a^{2} = b^{2} + c^{2} - 2 b c \cos A$ cho tam giác tương ứng.

c) Suy ra từ b, lưu ý rằng: ${\begin{cases} \cos \hat{A M C} + \cos \hat{A M B} = 0 \\ M B = M C = \frac{B C}{2} \end{cases}$

Lời giải:

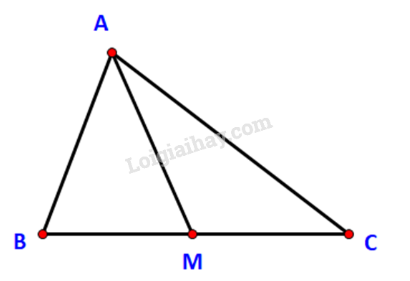
Toán lớp 10 Bài tập cuối chương III I Kết nối tri thức với cuộc sống (ảnh 1)

a) Ta có: $\hat{A M B} + \hat{A M C} = 180^{o}$

$\Rightarrow \cos \hat{A M B} = - \cos \hat{A M C}$

Hay $\cos \hat{A M B} + \cos \hat{A M C} = 0$

b) Áp dụng định lí cos trong tam giác AMB ta có:

$\begin{array}{l} A B^{2} = M A^{2} + M B^{2} - 2 M A . M B \cos \hat{A M B} \\ \Leftrightarrow M A^{2} + M B^{2} - A B^{2} = 2 M A . M B \cos \hat{A M B} (1) \end{array}$

Tương tự, Áp dụng định lí cos trong tam giác AMB ta được:

$\begin{array}{l} A C^{2} = M A^{2} + M C^{2} - 2 M A . M C \cos \hat{A M C} \\ \Leftrightarrow M A^{2} + M C^{2} - A C^{2} = 2 M A . M C \cos \hat{A M C} (2) \end{array}$

c) Từ (1), suy ra $M A^{2} = A B^{2} - M B^{2} + 2 M A . M B \cos \hat{A M B}$

Từ (2), suy ra $M A^{2} = A C^{2} - M C^{2} + 2 M A . M C \cos \hat{A M C}$

Cộng vế với vế ta được:

$2 M A^{2} = (A B^{2} - M B^{2} + 2 M A . M B \cos \hat{A M B}) + (A C^{2} - M C^{2} + 2 M A . M C \cos \hat{A M C})$

$\Leftrightarrow 2 M A^{2} = A B^{2} + A C^{2} - M B^{2} - M C^{2} + 2 M A . M B \cos \hat{A M B} + 2 M A . M C \cos \hat{A M C}$

Mà: $M B = M C = \frac{B C}{2}$ (do AM là trung tuyến)

$\Rightarrow 2 M A^{2} = A B^{2} + A C^{2} - {(\frac{B C}{2})}^{2} - {(\frac{B C}{2})}^{2} + 2 M A . M B \cos \hat{A M B} + 2 M A . M B \cos \hat{A M C}$

$\Leftrightarrow 2 M A^{2} = A B^{2} + A C^{2} - 2. {(\frac{B C}{2})}^{2} + 2 M A . M B (\cos \hat{A M B} + \cos \hat{A M C})$

$\Leftrightarrow 2 M A^{2} = A B^{2} + A C^{2} - {\frac{B C}{2}}^{2}$

$\begin{array}{l} \Leftrightarrow M A^{2} = \frac{A B^{2} + A C^{2} - {\frac{B C}{2}}^{2}}{2} \\ \Leftrightarrow M A^{2} = \frac{2 (A B^{2} + A C^{2}) - B C^{2}}{4} \end{array}$ (đpcm)

Cách 2:

Theo ý a, ta có: $\cos \hat{A M C} = - \cos \hat{A M B}$

Từ đẳng thức (1): suy ra $\cos \hat{A M B} = \frac{M A^{2} + M B^{2} - A B^{2}}{2. M A . M B}$

$\Rightarrow \cos \hat{A M C} = - \cos \hat{A M B} = - \frac{M A^{2} + M B^{2} - A B^{2}}{2. M A . M B}$

Thế $\cos \hat{A M C}$ vào biểu thức (2), ta được:

$M A^{2} + M C^{2} - A C^{2} = 2 M A . M C . (- \frac{M A^{2} + M B^{2} - A B^{2}}{2. M A . M B})$

Lại có: $M B = M C = \frac{B C}{2}$ (do AM là trung tuyến)

$\begin{array}{l} \Rightarrow M A^{2} + {(\frac{B C}{2})}^{2} - A C^{2} = 2 M A . M B . (- \frac{M A^{2} + M B^{2} - A B^{2}}{2. M A . M B}) \\ \Leftrightarrow M A^{2} + {(\frac{B C}{2})}^{2} - A C^{2} = - (M A^{2} + M B^{2} - A B^{2}) \\ \Leftrightarrow M A^{2} + {(\frac{B C}{2})}^{2} - A C^{2} + M A^{2} + {(\frac{B C}{2})}^{2} - A B^{2} = 0 \\ \Leftrightarrow 2 M A^{2} - A B^{2} - A C^{2} + {\frac{B C}{2}}^{2} = 0 \\ \Leftrightarrow 2 M A^{2} = A B^{2} + A C^{2} - {\frac{B C}{2}}^{2} \\ \Leftrightarrow M A^{2} = \frac{A B^{2} + A C^{2} - {\frac{B C}{2}}^{2}}{2} \\ \Leftrightarrow M A^{2} = \frac{2 (A B^{2} + A C^{2}) - B C^{2}}{4} \end{array}$