Toán 10 Cánh Diều trang 63 Bài 1: Toạ độ của vecto

Giang Ngày: 14-02-2023 Lớp 10

269

Với giải Câu hỏi trang 63 Toán 10 Tập 2 Cánh Diều trong Bài 1: Toạ độ của vecto giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Cánh Diều trang 63 Bài 1: Toạ độ của vecto

Hoạt động 4 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ $\vec{u} = (a; b)$ . Ta chọn điểm A sao cho $\vec{O A} = \vec{u}$ .

Xét vectơ đơn vị $\vec{i}$ trên trục hoành Ox và vectơ đơn vị $\vec{j}$ trên trục tung Oy (Hình 12).

(ảnh 1)

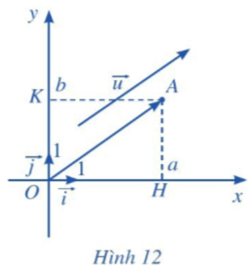
a) Tìm hoành độ và tung độ của điểm A.

b) Biểu diễn vectơ $\vec{O H}$ qua vectơ $\vec{i}$ .

c) Biểu diễn vectơ $\vec{O K}$ qua vectơ $\vec{j}$ .

d) Chứng tỏ rằng $\vec{u} = a \vec{i} + b \vec{j}$ .

Lời giải:

a) Ta có: $\vec{O A} = \vec{u}$ , mà (a; b) là tọa độ của vectơ $\vec{u}$ nên điểm A có hoành độ là a và tung độ là b.

b) Điểm H biểu diễn số a trên trục Ox nên $\vec{O H} = a \vec{i}$ .

c) Điểm K biểu diễn số b trên trục Oy nên $\vec{O K} = b \vec{j}$ .

d) Áp dụng quy tắc hình bình hành ta có: $\vec{O A} = \vec{O K} + \vec{O H}$ .

Mà $\vec{O H} = a \vec{i}$ , $\vec{O K} = b \vec{j}$ nên $\vec{O A} = a \vec{i} + b \vec{j}$ .

Theo bài ra ta có: $\vec{O A} = \vec{u}$ .

Vậy $\vec{u} = a \vec{i} + b \vec{j}$ .

Luyện tập 2 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm B(– 1; 0) và vectơ $\vec{v}$ = (0; – 7).

a) Biểu diễn $\vec{v}$ vectơ qua hai vectơ $\vec{i}$ và $\vec{j}$ .

b) Biểu diễn $\vec{O B}$ vectơ qua hai vectơ $\vec{i}$ và $\vec{j}$ .

Lời giải:

a) Vì $\vec{v}$ = (0; – 7) nên $\vec{v} = 0. \vec{i} + (- 7) . \vec{j} = - 7 \vec{j}$ .

b) Vì điểm B có tọa độ là (– 1; 0) nên $\vec{O B} = (- 1; 0)$ . Do đó:

$\vec{O B} = (- 1) . \vec{i} + 0. \vec{j} = - \vec{i}$ .

Xem thêm các lời giải SGK Toán 10 Cánh Diều hay, chi tiết khác:

Câu hỏi khởi động trang 60 Toán lớp 10 Tập 2: Hình 1 minh họa hoạt động của một màn hình ra đa ở trạm kiểm...

Hoạt động 1 trang 60 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy (Hình 2), hãy...

Hoạt động 2 trang 61 Toán lớp 10 Tập 2: Cho điểm M trong mặt phẳng tọa độ Oxy...

Hoạt động 3 trang 61 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ (Hình 7). Hãy xác định điểm A sao cho...

Luyện tập 1 trang 62 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ $\vec{c}, \vec{d}$ trong Hình 11...

Hoạt động 4 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ $\vec{u} = (a; b)$ . Ta chọn điểm A sao cho $\vec{O A} = \vec{u}$ ...

Luyện tập 2 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm B(– 1; 0) và vectơ $\vec{v}$ = (0; – 7)...

Hoạt động 5 trang 64 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A, B (Hình 13)...

Luyện tập 3 trang 64 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho các điểm: A(1; 3), B(5; – 1), C(2; – 2), D(– 2; 2)...

Bài 1 trang 65 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ trong Hình 16 và biểu diễn mỗi vectơ đó qua...

Bài 2 trang 65 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ sau...

Bài 3 trang 65 Toán lớp 10 Tập 2: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau...

Bài 4 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2; 3), B(– 1; 1), C(3; – 1)...

Bài 5 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho điểm M(– 1; 3)...

Bài 6 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 3; 1), B(– 1; 3), I(4; 2)...

Bài 7 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1; – 2), N(4; – 1) và P(6; 2)..

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương