Với giải Câu hỏi trang 64 Toán 10 Tập 2 Cánh Diều trong Bài 1: Toạ độ của vecto giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Cánh Diều trang 64 Bài 1: Toạ độ của vecto
Hoạt động 5 trang 64 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A, B (Hình 13).
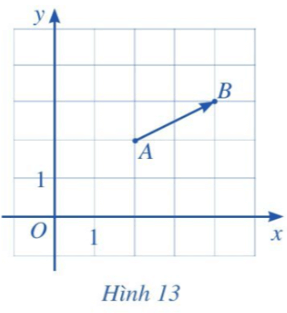
a) Tìm hoành độ xA và tung độ yA của điểm A; hoành độ xB và tung độ yB của điểm B.
b) Tìm điểm M sao cho . Từ đó, tìm hoành độ a và tung độ b của vectơ .
c) So sánh: xB – xA và a; yB – yA và b.
Lời giải:
a) Từ A và B ta kẻ các đường thẳng vuông góc với trục tung và trục hoành.
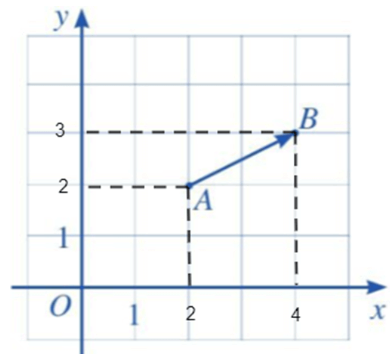
Ta xác định được tọa độ của các điểm A và B.
Hoành độ của điểm A là xA = 2, tung độ của điểm A là yA = 2.
Hoành độ của điểm B là xB = 4, tung độ của điểm B là yB = 3.
b) Để xác định điểm M, ta làm như sau:
- Từ đểm O, kẻ đường thẳng d song song với giá của vectơ (chính là đường thẳng AB).
- Lấy điểm M trên đường thẳng d sao cho hai vectơ cùng hướng và độ dài đoạn thẳng OM bằng độ dài vectơ (chính là độ dài đoạn thẳng AB).
Ta xác định được điểm M thỏa mãn như hình vẽ:
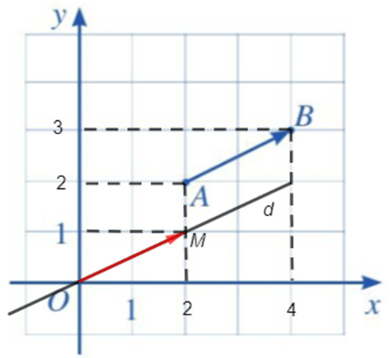
Từ điểm M, kẻ đường thẳng vuông góc với trục hoành, đường thẳng này cắt trục hoành tại điểm ứng với số 2, nên hoành độ của điểm M là xM = 2.
Từ điểm M, kẻ đường thẳng vuông góc với trục tung, đường thẳng này cắt trục tung tại điểm ứng với số 1, nên tung độ của điểm M là yM = 1.
Tọa độ của điểm M chính là tọa độ của vectơ nên .
Lại có , do đó tọa độ của vectơ là (2; 1).
Vậy hoành độ của vectơ là a = 2 và tung độ của vectơ là b = 1.
c) Ta có: xB – xA = 4 – 2 = 2 và a = 2 nên xB – xA = a.
Và yB – yA = 3 – 2 = 1 và b = 1 nên yB – yA = b.
Chứng minh .
Lời giải:
Ta có: . Do đó .
Lại có: . Do đó
Xem thêm các lời giải SGK Toán 10 Cánh Diều hay, chi tiết khác:
Hoạt động 1 trang 60 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy (Hình 2), hãy...
Hoạt động 2 trang 61 Toán lớp 10 Tập 2: Cho điểm M trong mặt phẳng tọa độ Oxy...
Luyện tập 1 trang 62 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ trong Hình 11...
Hoạt động 4 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ . Ta chọn điểm A sao cho ...
Hoạt động 5 trang 64 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A, B (Hình 13)...
Bài 2 trang 65 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ sau...
Bài 3 trang 65 Toán lớp 10 Tập 2: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau...
Bài 5 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho điểm M(– 1; 3)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
