Với giải Câu hỏi trang 70 SBT Toán 10 Tập 2 Chân trời sáng tạo trong Bài 3: Đường tròn trong mặt phẳng toạ độ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:
SBT Toán 10 Chân trời sáng tạo trang 70 Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 2 trang 70 SBT Toán 10: Lập phương trình đường tròn trong các trường hợp sau:
a) có tâm và bán kính
b) có đường kính AB với và
c) có tâm và tiếp xúc với đường thẳng
d) có tâm và đi qua điểm
Phương pháp giải:
Viết phương trình đường tròn tâm và bán kính R là
Lời giải:
a) có tâm và bán kính
Phương trình đường tròn:
b) có đường kính AB với và
+ I là trung điểm của AB nên
+
+ Phương trình đường tròn:
c) có tâm và tiếp xúc với đường thẳng
+
+ Phương trình đường tròn:
d) có tâm và đi qua điểm
+
+ Phương trình đường tròn:
Bài 3 trang 70 SBT Toán 10: Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh là:
a)
b)
Phương pháp giải:
Tâm đường tròn ngoại tiếp tam giác là điểm cách đều 3 đỉnh của tam giác
Lời giải:
a) à Tam giác ABC vuông tại A à I là trung điểm của BC
Phương trình đường tròn:
b) à Tam giác OPR vuông tại O à I là trung điểm của PR
Phương trình đường tròn:
Bài 4 trang 70 SBT Toán 10: Lập phương trình đường tròn tiếp xúc với hai trục tọa độ và đi qua điểm
Phương pháp giải:
Lời giải:
Gọi đường tròn (C) cần lập có tâm và bán kính R.
+ tiếp xúc với
Mặt khác: (C) tiếp xúc với nên nó thuộc một trong bốn góc phần tư của mặt phẳng.
=>(C) thuộc góc phần tư thứ nhất => =>
+ hoặc .
+ Phương trình đường tròn là hoặc
Bài 5 trang 70 SBT Toán 10: Cho đường tròn có phương trình
a) Chứng tỏ rằng điểm thuộc đường tròn
b) Viết phương trình tiếp tuyến với tại điểm
c) Viết phương trình tiếp tuyến với song song với đường thẳng
Phương pháp giải:
+ Phương trình tiếp tuyến d của đường tròn tại A có vectơ pháp tuyến
Lời giải:
có phương trình
(C) có tâm I(3;2) và bán kính R=5.
a) thuộc (C) vì
b) + VTPT của PT tiếp tuyến tại A là
PT tiếp tuyến tại A là
c) +
+
Vậy hoặc
Bài 6 trang 70 SBT Toán 10: Một cái cổng bán nguyệt rộng 6,8m, cao 3,4m. Mặt đường dưới cổng được chia thành hai làn cho xe ra vào
a) Viết phương trình mô phỏng cái cổng
b) Một chiếc xe tải rộng 2,4 m và cao 2,5 m đi đúng làn đường quy định có thể đi qua cổng được hay không?
Phương pháp giải:
Viết phương trình đường tròn tâm và bán kính R là
Lời giải:
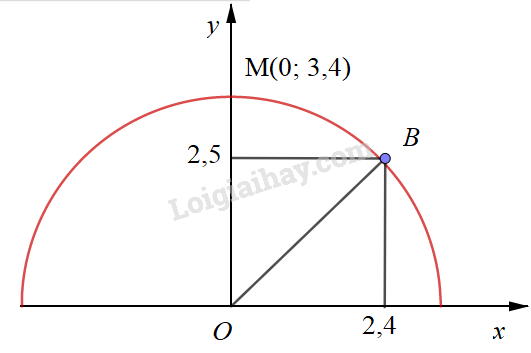
a) Chọn hệ tọa độ sao cho tâm của cái cổng hình bán nguyệt có tọa độ
Cộng rộng 6,8m, cao 3,4m nên đỉnh của cổng có tọa độ
Ta có phương trình mô phỏng cổng là:
b) chiếc xe tải rộng 2,4 m và cao 2,5 m
Khi đó thiết diện của xe tải là hình chữ nhật dài 2,5m và rộng 2,4m.
Gọi , khi đó thiết diện xe là hình chữ nhật OABC với A(2,4;0) và C(0;2,5).
Xe có thể đi qua cổng nếu hình chữ nhật nằm phía trong đường tròn hay OB <R=3,4.
Ta có:
Vậy nếu đi đúng làn đường quy định thì xe tải không thể đi qua cổng
Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2 trang 70 SBT Toán 10: Lập phương trình đường tròn trong các trường hợp sau...
Bài 3 trang 70 SBT Toán 10: Lập phương trình đường tròn ngoại tiếp tam giác có tọa độ các đỉnh...
Bài 4 trang 70 SBT Toán 10: Lập phương trình đường tròn tiếp xúc với hai trục tọa độ và đi qua điểm ...
Bài 5 trang 70 SBT Toán 10: Cho đường tròn có phương trình ...
Bài 6 trang 70 SBT Toán 10: Một cái cổng bán nguyệt rộng 6,8m, cao 3,4m....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.