Với giải Luyện tập – vận dụng 2 trang 41 SGK Toán 10 tập 1 Cánh Diều chi tiết trong Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng - Toán 10 Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Vẽ đồ thị mỗi hàm số bậc hai sau: a) y=x^2-4x-3
Luyện tập – vận dụng 2 trang 41 SGK Toán 10 tập 1 :Vẽ đồ thị mỗi hàm số bậc hai sau:
a)
b)
c)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục .
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số .
Lời giải:
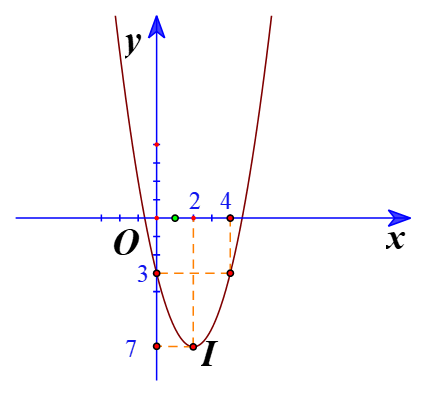
a) Đồ thị hàm số có đỉnh
Trục đối xứng là x=2
Giao điểm của parabol với trục tung là (0;-3)
Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
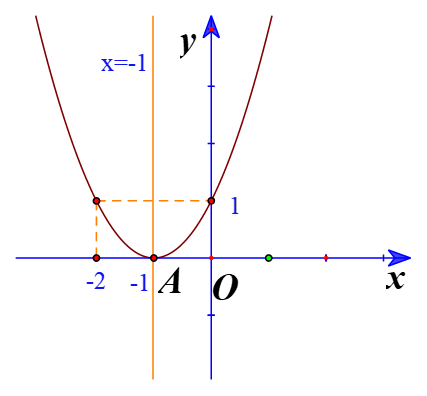
b) Đồ thị hàm số có đỉnh
Trục đối xứng là x=-1
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
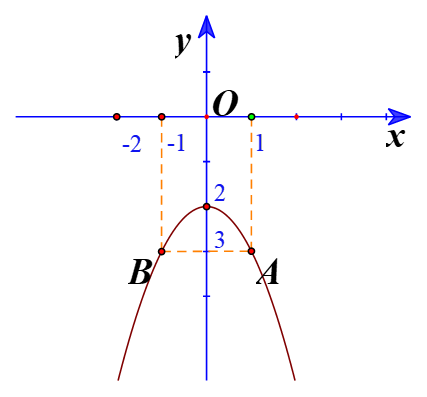
c) Đồ thị hàm số có đỉnh
Trục đối xứng là x=0
Giao điểm của parabol với trục tung là (0;-2)
Cho x=1=>y=-3
=> Điểm A(1;-3) thuộc đồ thị.
Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3).
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
Xem thêm các bài giải Toán 10 Cánh diều hay, chi tiết khác:
Câu hỏi khởi động trang 39 SGK Toán 10 tập 1 :Cầu cảng Sydney là một trong những hình ảnh biểu tượng của thành phố Sydney và nước Australia.
Hoạt động 1 trang 39 SGK Toán 10 tập 1 :Cho hàm số .
Luyện tập - vận dụng 1 trang 39 SGK Toán 10 tập 1 :Cho hai ví dụ về hàm số bậc hai.
Hoạt động 2 trang 39, 40 SGK Toán 10 tập 1 :Cho hàm số .
Hoạt động 3 trang 40 SGK Toán 10 tập 1 :Cho hàm số .
Luyện tập – vận dụng 3 trang 42 SGK Toán 10 tập 1 :Lập bảng biến thiên của mỗi hàm số sau:
Bài 2 trang 43 SGK Toán 10 tập 1 :Xác định parabol trong mỗi trường hợp sau:
Bài 3 trang 43 SGK Toán 10 tập 1 :Vẽ đồ thị của mỗi hàm số sau:
Bài 4 trang 43 SGK Toán 10 tập 1 :Cho đồ thị hàm số bậc hai ở Hình 15.
Bài 5 trang 43 SGK Toán 10 tập 1 :Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
