Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về khái niệm về phép dời hình và hai hình bằng nhau lớp 11.
Giải bài tập Toán 11 Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
Trả lời câu hỏi giữa bài:
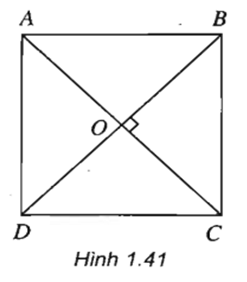
Lời giải:
Gợi ý. Sử dụng tính chất điểm nằm giữa hai điểm và khi và chỉ khi (h.1.43).
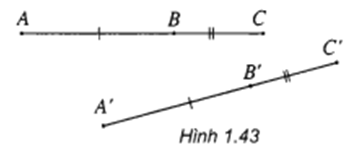
Phương pháp giải:
Áp dụng định nghĩa: phép dời hình là phép biến hình bảo toàn khoảng cảnh giữa hai điểm bất kỳ.
Lời giải:
Gọi ảnh của 3 điểm qua phép dời hình là 3 điểm
Phép dời hình là phép biến hình bảo toàn khoảng cảnh giữa hai điểm bất kỳ nên:
Ta có: thằng hàng và nằm giữa và
Hay thẳng hàng và nằm giữa và
+) Phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì.
+) Biến ba điểm thằng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
Lời giải:
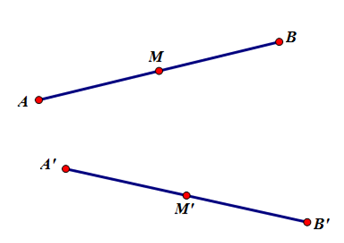
Gọi lần lượt là ảnh của qua phép dời hình
Theo tính chất 1 ta có: và ; Ba điểm thẳng hàng, trong đó nằm giữa.
là trung điểm
Kết hợp (1) là trung điểm
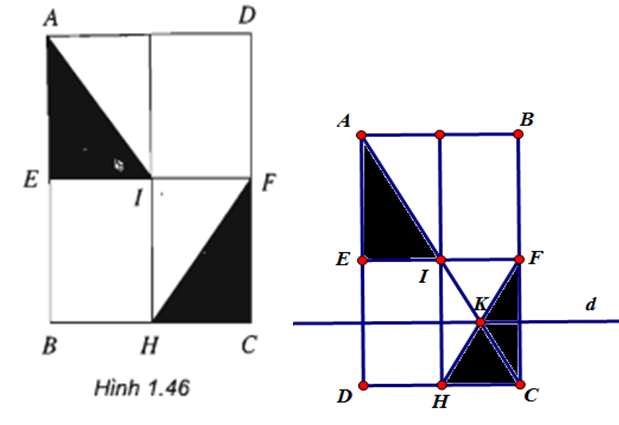
Lời giải:
- Phép đối xứng qua tâm biến:
+) thành
+) thành
+) thành
Nên biến thành
- Phép đối xứng qua trục là đường thẳng biến:
+) thành
+) thành
+) thành
Do đó biến thành
Vậy phép dời hình cần tìm là hợp của hai phép đối xứng tâm và đối xứng trục qua đường thẳng
Lời giải:
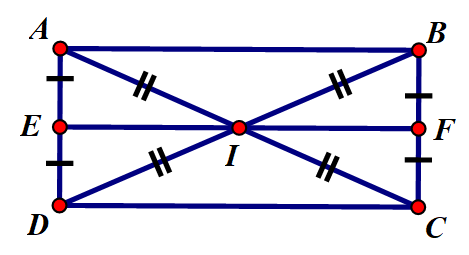
là giao điểm và nên là trung điểm của và
Mà
Gọi theo thứ tự là trung điểm của và là đường trung bình của hình chữ nhật và
vuông góc với và vuông góc với
Xét hai tam giác vuông và có:
(cạnh huyền – cạnh góc vuông)
(hai cạnh tương ứng)
là trung điểm
Do đó, phép đối xứng qua tâm biến hình thang thành hình thang
⇒ Hai hình thang và bằng nhau.
Bài tập trang 23, 24 SGK Toán 11
a) Chứng minh rằng các điểm và theo thứ tự là ảnh của và qua phép quay tâm góc .
b) Gọi tam giác là ảnh của tam giác qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm góc và phép đối xứng qua trục . Tìm tọa độ các đỉnh của tam giác .
Phương pháp giải:
a) Sử dụng định nghĩa phép quay
b) Thực hiện liên tiếp phép quay tâm góc quay và phép đối xứng trục trên mặt phẳng tọa độ
Lời giải:
a)
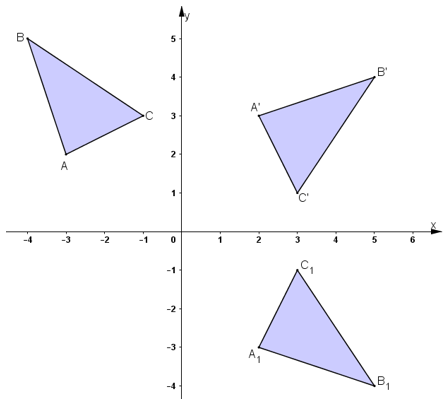
Ta có:
Tương tự ta cũng có .
Chú ý:
Cách giải tham khảo (công thức mở rộng)
Sử dụng biểu thức tọa độ của phép quay: Ảnh của điểm qua phép quay tâm góc quay là điểm với thỏa mãn hệ phương trình
(hình bên)
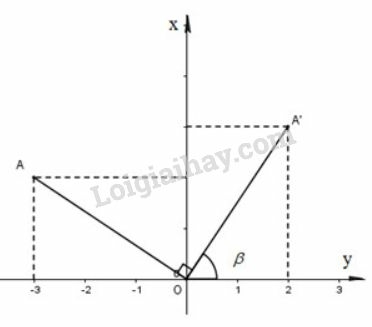
Phép quay tâm góc biến điểm thành điểm với
lần lượt là ảnh của qua phép quay tâm góc quay .
b)
(Hình 1.26)
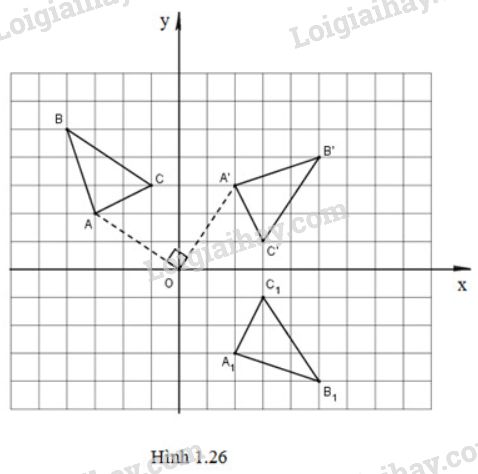
Gọi tam giác là ảnh của tam giác qua phép đối xứng trục .
Khi đó,
Vậy
Gọi L là trung điểm của OF, thực hiện liên tiếp hai phép biến hình sau:
- Phép đối xứng trục EO.
- Phép tịnh tiến theo .
Các phép tịnh tiến và phép đối xứng trục hình không làm thay đổi khoảng cách giữa hai điểm bất kì.
Lời giải:
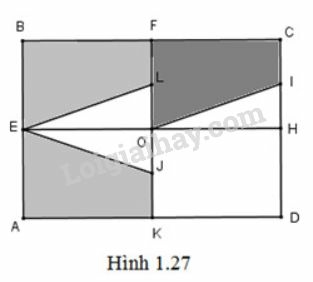
Gọi L là trung điểm của OF.
+ Vì EO là đường trung trực của các đoạn thẳng AB; KF; JL
⇒ B = ĐEO (A); F = ĐEO (K) ; L = ĐEO (J); E = ĐEO (E)
⇒ Hình thang BFLE là ảnh của hình thang AKJE qua phép đối xứng trục EO.
⇒ Hai hình thang BFLE và AKJE bằng nhau (1).
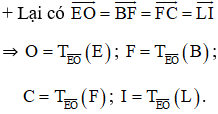
⇒ Hình thang FCIO là ảnh của hình thang BFLE qua phép tịnh tiến theo
⇒ Hai hình thang FCIO và BFLE bằng nhau (2)
Từ (1) và (2) ⇒ hai hình thang FCIO và AKJE bằng nhau
Lời giải:
Gọi phép dời hình đó là .
Gọi M, N là trung điểm của AB, AC, G là trọng tâm của tam giác ABC.
Do biến thành nên f biến thành là trung điểm của của .
Vậy biến các trung tuyến của tam giác tương ứng thành các trung tuyến của tam giác .
Do đó f biến G là giao điểm của CM, BN thành G' là giao điểm của C'M', B'N' hay G' là trọng tâm tam giác A'B'C'.
Từ đó suy ra biến trọng tâm của tam giác thành trọng tâm của tam giác .
Cách khác:
Gọi f là phép dời hình biến tam giác ABC thành tam giác A’B’C’.
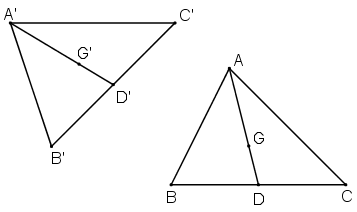
Gọi D là trung điểm của BC, D’ = f(D).
Gọi G là trọng tâm ΔABC, G’ = f(G).
+ B, D, C thẳng hàng ⇒ B’; D’; C’ thẳng hàng.
+ A; G; D thẳng hàng ⇒ A’; G’; D’ thẳng hàng.
+ B’D’ = BD = BC/2 = B’C’/2 ⇒ D’ là trung điểm B’C’.
+ A’G’ = AG = 2.AD/3 = 2.A’D’/3 ⇒ G’ là trọng tâm ΔA’B’C’.
Vậy phép dời hình f biến trọng tâm G của ΔABC thành trọng tâm G’ của ΔA’B’C’ (đpcm).
Lý thuyết Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
1. Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì. Nghĩa là với hai điểm tùy ý và ảnh tương ứng của chúng, ta luôn có
2. Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng trục, đối xứng tâm và phép quay là những phép dời hình.
3. Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình là một phép dời hình.
4. Phép dời hình có các tính chất:
a, Biến ba điểm thằng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.
b, Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn bằng nó.
c, Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.
d, Biến đường tròn thành đường tròn có cùng bán kính.
5. Nếu một phép dời hình biến tam giác thành tam giác thì nó cũng biến trọng tâm, trực tâm, tâm các đường trọn nội tiếp, ngoại tiếp.. của tam giác tương ứng thành trọng tâm, trực tâm, tâm các đường trọng nội tiếp, ngoại tiếp... của tam giác .
6. Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.