Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 8: Phép đồng dạng chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về phép đồng dạng lớp 11.
Giải bài tập Toán 11 Bài 8: Phép đồng dạng
Trả lời câu hỏi giữa bài:
Lời giải:
Phép vị tự tâm , tỉ số biến điểm thành 2 điểm sao cho:
Nếu thực hiện liên tiếp phép đồng dạng tỉ số và phép đồng dạng tỉ số ta được phép đồng dạng tỉ số
Lời giải:
- Phép đồng dạng tỉ số biến 2 điểm thành 2 điểm sao cho
- Phép đồng dạng tỉ số biến 2 điểm thành 2 điểm sao cho
Vậy: Nếu thực hiện liên tiếp phép đồng dạng tỉ số và phép đồng dạng tỉ số ta được phép đồng dạng tỉ số
Lời giải:
Phép đồng dạng tỉ số biến 3 điểm thẳng hàng thành 3 điểm sao cho:
thẳng hàng và nằm giữa
Do đó hay
thẳng hàng và nằm giữa .
Cần chứng minh:
+)
+) thẳng hàng.
Lời giải:
Gọi lần lượt là ảnh của qua phép đồng dạng tỉ số
là trung điểm hay
Lại có thẳng hàng nên thẳng hàng.
Vậy là trung điểm của
Lời giải:
Hai đường tròn bất kì đồng dạng với nhau.
Hai hình vuông bất kì đồng dạng với nhau.
Hai hình chữ nhật bất kì chưa chắc đồng dạng với nhau vì tỉ lệ các kích thước tương ứng chưa chắc bằng nhau.
Bài tập trang 33 SGK Toán 11
B1: xác định ảnh của tam giác qua phép vị tự
B2: xác định ảnh của tam giác qua phép đối xứng
Lưu ý: để tìm ảnh của tam giác qua phép dời hình, ta tìm ảnh của từng đỉnh. Các đỉnh mới tạo thành ảnh của tam giác qua phép dời hình đó.
Lời giải:
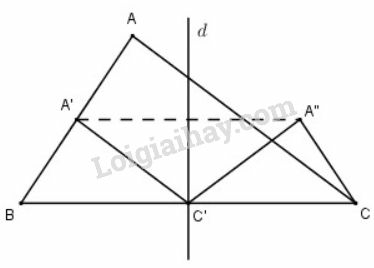
là trung điểm của
Tương tự ta có thì C'\) là trung điểm của
Do đó .
Dọi là đường trung trực của Khi đó,
; ;
Nên phép đối xứng qua đường trung trực của biến thành .
Vậy ảnh của tam giác qua phép đồng dạng đã cho là tam giác .
Thực hiện liên tiếp hai phép biến hình sau:
- Phép vị tự tâm tỉ số
- Phép đối xứng tâm
Lời giải:
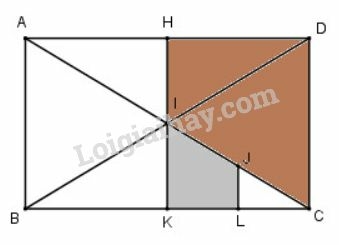
Ta có: là trung điểm của nên
Do đó .
Lại có,
Nên .
Do đó tồn tại phép đồng dạng (hợp bởi phép vị tự và phép đối xứng tâm) biến hình thang thành hình thang .
Vậy hai hình thang và hình thang đồng dạng.
Cách khác:
+ là trung điểm
Hình thang đối xứng với hình thang qua (1)
+ lần lượt là trung điểm của
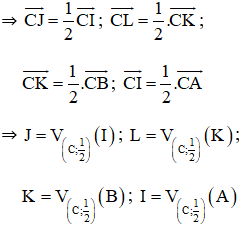
Hình thang là ảnh của hình thang qua phép vị tự tâm tỉ số
Hình thang là ảnh của hình thang qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm và phép vị tự tâm tỉ số .
và đồng dạng.
Phép quay tâm , góc quay biến đường tròn tâm bán kính thành đường tròn tâm bán kính , với .
Phép vị tự tâm , tỉ số biến đường tròn tâm , bán kính thành đường tròn tâm ; bán kính , với .
Lời giải:
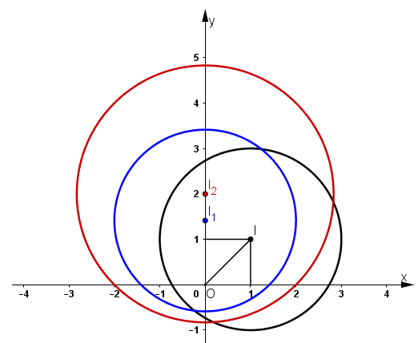
+ Gọi (Phép quay đường tròn tâm bán kính qua tâm một góc
Xác định :
Ta có:
+ Gọi ta có:
Do đó phép vị tự tâm , tỉ số biến đường tròn tâm , bán kính R thành đường tròn tâm ; bán kính .
Vậy phương trình đường tròn tâm , bán kính là .
Chú ý:
Cách khác để tìm (chỉ dùng cho trắc nghiệm) như sau:
Gọi ta có:
.
Thực hiện liên tiếp hai phép biến hình:
- Phép đối xứng qua đường thẳng với là phân giác của góc
- Phép vị tự tâm tỉ số
Lời giải:
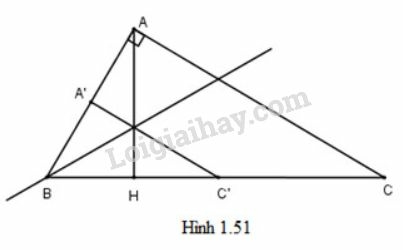
Gọi là đường phân giác của .
Gọi .
Dễ thấy .
Ta có biến thành .
Suy ra = nên góc
Theo định lý Ta-let có
Mà nên .
Do đó phép đồng dạng có được bằng cách thực hiện liên tiếp và sẽ biến thành .
Lý thuyết Bài 8: Phép đồng dạng
1. Định nghĩa
Phép biến hình được gọi là phép đồng dạng tỉ số , , nếu với hai điểm bất kì và ảnh tương ứng của chúng, ta luôn có
2. Nhận xét
a) Phép dời hình là phép đồng dạng tỉ số
b) Phép vị tự tỉ số là phép đồng dạng tỉ số
c) Nếu thực hiện liên tiếp phép đồng dạng tỉ số và phép đồng dạng tỉ số ta được phép đồng dạng tỉ số
d) Phép đồng dạng tỉ số là hợp thành của một phép dời hình và một phép vị tự tỉ số hoặc . Nó cũng là hợp thành của một phép vị tự tỉ số hoặc và một phép dời hình
3. Tính chất
Phép đồng dạng tỉ số có các tính chất:
a) Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữ các điểm ấy.
b) Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng có độ dài bằng thành đoạn thẳng có độ dài bằng .
c) Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là , biến góc thành góc bằng nó.
- Nếu một phép đồng dạng biến tam giác thành tam giác thì nó cũng biến trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiến của tam giác thành các vị trí đó trong tam giác .
d) Biến đường tròn bán kính thành đường tròn bán kính .
e) Biến đa giác cạnh thành đa giác cạnh, đỉnh thành đỉnh, cạnh thành cạnh.
4. Hai hình đồng dạng
Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.