Giải Toán 11 trang 111 Tập 1 (Kết nối tri thức)

Giải Toán 11 trang 111 Tập 1 (Kết nối tri thức)

Ngọc Nguyễn Ngày: 05-02-2024 Lớp 11

197

Với giải SGK Toán 11 Kết nối tri thức trang 111 chi tiết trong Bài 16: Giới hạn của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 111 Tập 1 (Kết nối tri thức)

Mở đầu trang 111 Toán 11 Tập 1: Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức

$m = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$ ,

trong đó m₀ là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?

Lời giải:

Sau bài học này ta sẽ giải quyết được bài toán trên như sau:

Từ công thức khối lượng $m = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$

ta thấy m là một hàm số của v, với tập xác định là nửa khoảng [0; c). Rõ ràng khi v tiến gần tới vận tốc ánh sáng, tức là v ⟶ c, ta có $\sqrt{1 - \frac{v^{2}}{c^{2}}} \to 0$ . Do đó $\lim_{v \to c^{-}} m (v) = + \infty$ , nghĩa là khối lượng m của vật trở nên vô cùng lớn khi vận tốc của vật gần tới vận tốc ánh sáng.

1. Giới hạn hữu hạn của một hàm số tại một điểm

HĐ1 trang 111 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại một điểm

Cho hàm số $f (x) = \frac{4 - x^{2}}{x - 2}$ .

a) Tìm tập xác định của hàm số f(x).

b) Cho dãy số $x_{n} = \frac{2 n + 1}{n}$ . Rút gọn f(x_n) và tính giới hạn của dãy (u_n) với u_n = f(x_n).

c) Với dãy số (x_n) bất kì sao cho x_n ≠ 2 và x_n ⟶ 2, tính f(x_n) và tìm $\lim_{n \to + \infty} f (x_{n})$ .

Lời giải:

a) Biểu thức f(x) có nghĩa khi x – 2 ≠ 0 ⇔ x ≠ 2.

Do đó, tập xác định của hàm số f(x) là D = ℝ \ {2}.

b) Ta có:

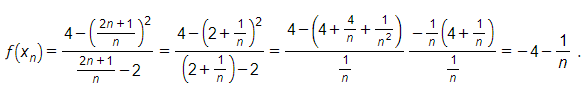
Toán 11 Bài 16 (Kết nối tri thức): Giới hạn của hàm số (ảnh 1)

$\lim_{n \to + \infty} u_{n} = \lim_{n \to + \infty} f (x_{n}) = \lim_{n \to + \infty} (- 4 - \frac{1}{n}) = - 4$ .

c) Ta có: $f (x_{n}) = \frac{4 - x_{n}^{2}}{x_{n} - 2} = \frac{(2 - x_{n}) (2 + x_{n})}{- (2 - x_{n})} = - 2 - x_{n}$ .

Vì x_n ≠ 2 và x_n ⟶ 2 với mọi n nên $\lim_{n \to + \infty} x_{n} = 2$ .

Do đó, $\lim_{n \to + \infty} f (x_{n})$ $= \lim_{n \to + \infty} (- 2 - x_{n}) = - 2 - 2 = - 4$ .

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 111 Toán 11 Tập 1: Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức

HĐ1 trang 111 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại một điểm Cho hàm số $f (x) = \frac{4 - x^{2}}{x - 2}$ .

Luyện tập 1 trang 113 Toán 11 Tập 1: Tính $\lim_{x \to 1} \frac{x - 1}{\sqrt{x} - 1}$ .

HĐ2 trang 113 Toán 11 Tập 1: Nhận biết khái niệm giới hạn một bên

Luyện tập 2 trang 113 Toán 11 Tập 1: Cho hàm số 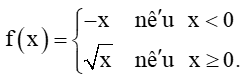Toán 11 (Kết nối tri thức) Bài 16: Giới hạn của hàm số (ảnh 5)

HĐ3 trang 114 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại vô cực

Luyện tập 3 trang 115 Toán 11 Tập 1: Tính $\lim_{x \to + \infty} \frac{\sqrt{x^{2} + 2}}{x + 1}$ .

Vận dụng trang 115 Toán 11 Tập 1: Cho tam giác OAB với A = (a; 0) và B = (0; 1) như Hình 5.5. Đường cao OH có độ dài là h.

HĐ4 trang 115 Toán 11 Tập 1:Nhận biết khái niệm giới hạn vô cực

HĐ5 trang 116 Toán 11 Tập 1: Cho hàm số $f (x) = \frac{1}{x - 1}$ . Với các dãy số (x_n) và (x'_n) cho bởi $x_{n} = 1 + \frac{1}{n}$ , ${x^{'}}_{n} = 1 - \frac{1}{n}$ , tính $\lim_{n \to + \infty} f (x_{n})$ và $\lim_{n \to + \infty} f ({x^{'}}_{n})$ .

Luyện tập 4 trang 116 Toán 11 Tập 1: Tính các giới hạn sau: a) 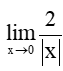Toán 11 (Kết nối tri thức) Bài 16: Giới hạn của hàm số (ảnh 9) ;

Bài 5.7 trang 118 Toán 11 Tập 1: Cho hai hàm số và g(x) = x + 1. Khẳng định nào sau đây là đúng?

Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau: a) $\lim_{x \to 0} \frac{{(x + 2)}^{2} - 4}{x}$ ;

Bài 5.9 trang 118 Toán 11 Tập 1: Cho hàm số Toán 11 (Kết nối tri thức) Bài 16: Giới hạn của hàm số (ảnh 13) (hàm Heaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/mở của dòng điện tại thời điểm t = 0).

Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên: a) $\lim_{x \to 1^{+}} \frac{x - 2}{x - 1}$ ;

Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số 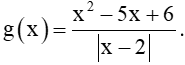Toán 11 (Kết nối tri thức) Bài 16: Giới hạn của hàm số (ảnh 14) .

Bài 5.12 trang 118 Toán 11 Tập 1:Tính các giới hạn sau: a) $\lim_{x \to + \infty} \frac{1 - 2 x}{\sqrt{x^{2} + 1}}$ ;

Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số $f (x) = \frac{2}{(x - 1) (x - 2)}$ .

Tính $\lim_{x \to 2^{+}} f (x)$ và $\lim_{x \to 2^{-}} f (x)$ .

Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Một vài áp dụng của toán học trong tài chính

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

291

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

312

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

340

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

288

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.