Với giải Bài 5.25 trang 124 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài tập cuối chương 5 giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Bài 5.25 trang 124 Toán 11 Tập 1 | Kết nối tri thức Giải Toán lớp 11
Bài 5.25 trang 124 Toán 11 Tập 1: Cho dãy số (un) có tính chất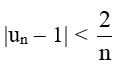 
. Có kết luận gì về giới hạn của dãy số này?
Lời giải:
Vì 
Do đó, . Từ đó suy ra .
Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (un) với . Mệnh đề đúng là
Bài 5.19 trang 123 Toán 11 Tập 1: Cho . Giới hạn của dãy số (un) bằng
Bài 5.20 trang 123 Toán 11 Tập 1: Cho cấp số nhân lùi vô hạn (un) với Tổng của cấp số nhân này bằng
Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số . Mệnh đề đúng là
Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số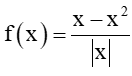
Khi đó bằng
Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số 
. Hàm số f(x) liên tục trên
Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số Hàm số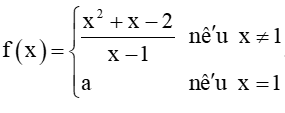 
liên tục tại x = 1 khi
Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau: a) ;
Bài 5.27 trang 124 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số.
Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau: a) ; b) ;
Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên: a)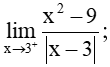 
Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn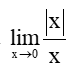 
không tồn tại.
Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho.
Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số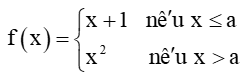
liên tục trên ℝ.
Xem thêm các bài giải sách giáo khoa Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
