Toptailieu.vn biên soạn và giới thiệu Phương pháp giải Phương trình bậc nhất hai ẩn và tập nghiệm (50 bài tập minh họa) hay, chi tiết nhất, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hỗn số, từ đó học tốt môn Toán 9.

Phương pháp giải Phương trình bậc nhất hai ẩn và tập nghiệm (50 bài tập minh họa)

I. Lý thuyết

1. Khái niệm phương trình bậc nhất hai ẩn

- Phương trình bậc nhất hai ẩn x, y là phương trình có dạng: ax + by = c

trong đó a, b, c là các số cho trước, $a\ne 0;b\ne 0$.

- Nếu số thực $x_0;y_0$ thỏa mãn $a{x}_0+b{y}_0=c$ thì cặp số $\left(x_0;y_0\right)$ được gọi là nghiệm của phương trình ax + by = c.

- Trong mặt phẳng tọa độ Oxy, mỗi nghiệm $\left(x_0;y_0\right)$ của phương trình ax + by = c được biểu diễn bởi điểm có tọa độ $\left(x_0;y_0\right)$.

2. Tập nghiệm của phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn ax + by =c luôn có vô số nghiệm.

Tập nghiệm của phương trình biểu diễn bởi đường thẳng d: ax + by = c

- Nếu $a\ne 0$ và b = 0 thì phương trình có nghiệm $\left\{\begin{array}{l}x=\frac{c}{a}\\ y\in ℝ\end{array}\right.$ và đường thẳng d song song hoặc trùng với trục tung.

- Nếu a = 0 và $b\ne 0$ thì phương trình có nghiệm $\left\{\begin{array}{l}x\in ℝ\\ y=\frac{c}{b}\end{array}\right.$ và đường thẳng d song song hoặc trùng với trục hoành.

- Nếu $a\ne 0;b\ne 0$ thì phương trình có nghiệm $\left\{\begin{array}{l}x\in ℝ\\ y=\frac{-a}{b}x+\frac{c}{b}\end{array}\right.$ hoặc $\left\{\begin{array}{l}y\in ℝ\\ x=\frac{-b}{a}y+\frac{c}{a}\end{array}\right.$ khi đó đường thẳng d cắt cả hai trục Ox; Oy. Đường thẳng d là đồ thị hàm số $y=\frac{-a}{b}x+\frac{c}{b}$.

II. Dạng bài tập và phương pháp giải

Dạng 1: Xét một cặp số cho trước có là nghiệm của phương trình bậc nhất hai ẩn không

Phương pháp giải: Nếu cặp số thực $\left(x_0;y_0\right)$ thỏa mãn $a{x}_0+b{y}_0=c$ thì nó được gọi là nghiệm của phương trình ax + by = c.

Ví dụ 1: Trong các cặp số (12; 1); (1; 1); (2; -3) cặp số nào là nghiệm của phương trình 2x – 5y =19.

Lời giải:

- Xét cặp số (12; 1)

Thay x = 12 và y = 1 ta có:

2.12 -1.5 = 24 – 5 = 19 nên cặp số (12; 1) là nghiệm của phương trình 2x – 5y = 19.

- Xét cặp số (1; 1) ta có:

Thay x = 1; y = 1 ta có:

2.1 – 5.1 = -3 nên cặp số (1; 1) không là nghiệm của phương trình 2x – 5y =19.

- Xét cặp số (2; -3)

Thay x = 2 và y = -3 ta có:

2.2 – 5.(-3) = 4 + 15 = 19 nên căp số (2; -3) là nghiệm của phương trình 2x – 5y = 19.

Ví dụ 2: Viết phương trình bậc nhất hai ẩn có hai nghiệm là (2; 0) và (-1; -2).

Lời giải:

Vì nghiệm của phương trình bậc nhất hai ẩn nằm trên một đường thẳng nên ta gọi đường thẳng đó là d: y = ax + b.

+ Thay x = 2; y = 0 vào đường thẳng d ta có: 0 = 2.a + b (1)

+ Thay x = -1; y = -2 vào đường thẳng d ta có: -2 = -1.a + b (2)

Từ (2) ta có: b = -2 + a thay vào (1) ta có:

2.a + a – 2 =0

$\iff$3a – 2 = 0

$\iff$3a = 2

$\iff a=\frac{2}{3}$$\Rightarrow b=-2+\frac{2}{3}=\frac{-4}{3}$

Đường thẳng d cần tìm là y = $\frac{2}{3}$x$-\frac{4}{3}$

$\Rightarrow$Phương trình bậc nhất hai ẩn là 2x – 3y – 4 = 0.

Dạng 2: Viết công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn và biểu diễn tập nghiệm phương trình trên mặt phẳng tọa độ

Phương pháp giải: Xét phương trình bậc nhất hai ẩn ax + by + c = 0.

- Để viết công thức nghiệm tổng quát của phương trình, trước tiên ta biểu diễn x theo y (hoặc y theo x) rồi đưa ra kết luận về công thức nghiệm tổng quát.

- Để biểu diễn tập nghiệm phương trình trên mặt phẳng tọa độ, ta vẽ đường thẳng d có phương trình ax + by = c trên mặt phẳng tọa độ.

Ví dụ 1: Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau:

a) 2x – 3y = 5

b) 4x +0y =12.

Lời giải:

a) Xét phương trình 2x – 3y = 5 ta có:

$a\ne 0;b\ne 0$ (do a = 2; b = -3) nên ta có công thức nghiệm của phương trình là

$\left\{\begin{array}{l}x\in ℝ\\ y=\frac{-a}{b}x+\frac{c}{b}\end{array}\right.$$\iff \left\{\begin{array}{l}x\in ℝ\\ y=\frac{2}{3}x-\frac{5}{3}\end{array}\right.$

Vẽ đường thẳng $y=\frac{2}{3}x-\frac{5}{3}$ trên hệ mặt phẳng tọa độ.

Cho x = 0 $\Rightarrow y=\frac{-5}{3}$$\Rightarrow A\left(0;\frac{-5}{3}\right)$

Cho y = 0$\Rightarrow x=\frac{5}{2}\Rightarrow B\left(\frac{5}{2};0\right)$

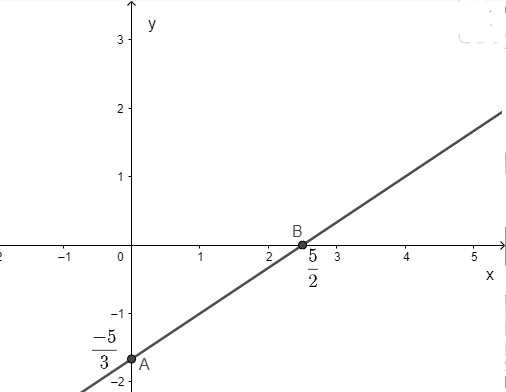
Nghiệm của phương trình 2x – 3y = 5 là đường thẳng được biểu diễn trên hình vẽ.

b) Xét phương trình 4x + 0y = 12

$a\ne 0;b=0$ (do a = 4; b = 0) nên ta có công thức nghiệm của phương trình là

$\left\{\begin{array}{l}x=\frac{c}{a}\\ y\in ℝ\end{array}\right.$$\iff \left\{\begin{array}{l}x=\frac{12}{4}=3\\ y\in ℝ\end{array}\right.$

Vẽ đường thẳng x = 3 trên hệ mặt phẳng tọa độ.

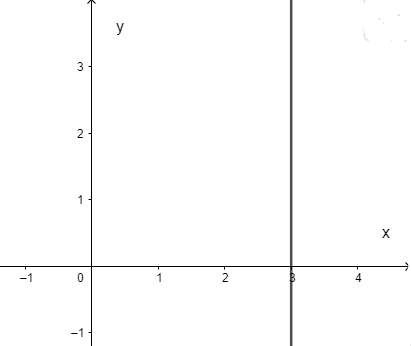
Dạng 3: Tìm điều kiện của tham số để đường thẳng thỏa mãn điều kiện cho trước

Phương pháp giải: Ta có thể sử dụng một số lưu ý sau đây để giải dạng toán này.

- Nếu $a\ne 0$ và b = 0 thì phương trình đường thẳng d: ax + by = c có dạng d: $x=\frac{c}{a}$khi đó d song song hoặc trùng với Oy.

- Nếu a = 0 và $b\ne 0$ thì phương trình đường thẳng d: ax + by = c có dạng d: $y=\frac{c}{b}$khi đó d song song hoặc trùng với Ox.

- Nếu $a\ne 0;b\ne 0$ thì phương trình đường thẳng d: ax + by = c có dạng d: $y=\frac{-a}{b}x+\frac{c}{b}$.

- Đường thẳng d: ax + by = c đi qua điểm $M\left(x_0;y_0\right)$ khi và chỉ khi $a{x}_0+b{y}_0=c$.

Ví dụ 1:  Cho đường thẳng d có phương trình: (m – 2)x + (3m – 1)y = 6m – 2

Tìm m để:

a) d song song hoặc trùng với trục hoành.

b) d song song hoặc trùng với trục tung

c) d đi qua điểm A(1; -1).

Lời giải:

a) Để d song song với trục hoành

$\iff \left\{\begin{array}{l}a=0\\ b\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}m-2=0\\ 3m-1\ne 0\end{array}\right.$

$\iff \left\{\begin{array}{l}m=2\\ 3m\ne 1\end{array}\right.$

$\iff \left\{\begin{array}{l}m=2\\ m\ne \frac{1}{3}\end{array}\right.$

Vậy m = 2 thì d song song với trục hoàng.

b) Để d song song với trục tung $\iff \left\{\begin{array}{l}a\ne 0\\ b=0\end{array}\right.$

$\iff \left\{\begin{array}{l}m-2\ne 0\\ 3m-1=0\end{array}\right.$

$\iff \left\{\begin{array}{l}m\ne 2\\ 3m=1\end{array}\right.$

$\iff \left\{\begin{array}{l}m\ne 2\\ m=\frac{1}{3}\end{array}\right.$

Vậy $m=\frac{1}{3}$thì d song song với trục tung.

c) d đi qua A(1; -1). Thay x = 1; y = -1 và d ta có:

(m - 2).1 + (3m – 1).(-1) = 6m – 2

$\iff m-2-3m+1=6m-2$

$\iff m-3m-2+1-6m+2=0$

$\iff -8m+1=0$

$\iff -8m=-1$

$\iff m=\frac{1}{8}$

Vậy $m=\frac{1}{8}$ thì d đi qua A(1; -1)

III. Bài tập tự luyện

Bài 1: Cặp số (-2; 3) là nghiệm của phương trình nào trong các phương trình dưới đây?

a) x – y = 1

b) 2x + 3y = 5

c) 2x + y = 7

d) 2x – y = -7

Bài 2: Trong các cặp số (1; 3); (-2; 0); (0; 4); (3; 2) cắp số nào là nghiệm của phương trình 2x + 2y = 8.

Bài 3: Tìm các giá trị của m để phương trình bậc nhất hai ẩn $\sqrt{m+1}x-2y=m+1$có một nghiệm là (1; -1).

Bài 4: Cho hai nghiệm của một phương trình bậc nhất hai ẩn là (2; 3) và (4; 6). Tìm phương trình bậc nhất hai ẩn đó.

Bài 5: Viết công thức tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ:

a) 3x – y = 5

b) 2x + 0y = 6

c) 0x + 3y = 9.

Bài 6: Cho đường thẳng d có phương trình:

(2m – 1)x +3(m – 1)y = 4m – 2

Tìm các tham số m để

a) d song song với Ox

b) d song song với Oy

c) d đi qua gốc tọa độ

d) d đi qua điểm A(2; 1).

Bài 7: Tìm giá trị của tham số m để cặp số $\left(\frac{-3}{2};2\right)$ là nghiệm của phương trình:

 (m – 3)x +2my = 5 + m

Bài 8: Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ:

a) x – 2y = 7

b) 3x – 2y = 3

c) 7x + 0y = 14.

Bài 9: Tìm phương trình đường thẳng d biết d đi qua hai điểm M(-1; -3) và N(2; 1).

Bài 10: Cho đường thẳng d có phương trình:

(2m – 3)x + (3m – 1)y = m + 2

a) d song song với Ox

b) d song song với Oy

c) d đi qua gốc tọa độ

d) d đi qua A(2; 3).

Xem thêm các dạng Toán 9 hay, chọn lọc khác:

Phương trình bậc nhất hai ẩn và tập nghiệm và cách giải bài tập

Hệ phương trình có chứa tham số và cách giải bài tập

Giải bài toán bằng cách lập hệ phương trình hay, chi tiết

Hệ thức giữa cạnh và đường cao trong tam giác vuông đầy đủ và cách giải

Các bài toán về Tỉ số lượng giác của góc nhọn và cách giải