Với Giải Bài 2 trang 65 sách bài tập Toán 8 Tập 1 trong Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều Sách bài tập Toán lớp 8 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 8.
Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD
Bài 2 trang 65 sách bài tập Toán 8 Tập 1: Cho hình bình hành ABCD. Gọi H và K lần lượt là chân đường cao hạ từ A và C đến BD.
a) Chứng minh rằng tứ giác AHCK là hình bình hành.
b) Gọi M là giao điểm của AK và BC, N là giao điểm của CH và AD. Chứng minh AN = CM.
c) Gọi O là trung điểm của HK. Chứng minh M, O, N thẳng hàng.
Lời giải:
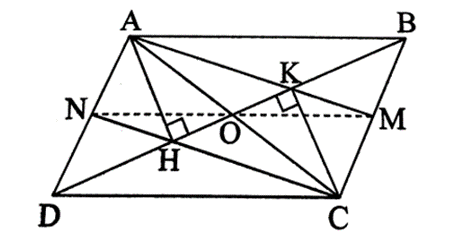
a) Do ABCD là hình bình hành nên AB // CD
Suy ra (hai góc so le trong) hay .
Xét ∆AHB vuông tại H và ∆CKD vuông tại K, ta có:
AB = CD (do ABCD là hình bình hành); (chứng minh trên).
Suy ra ∆AHB = ∆CKD (cạnh huyền – góc nhọn)
Do đó AH = CK (hai cạnh tương ứng)
Ta có: AH ⊥ BD, CK ⊥ BD suy ra AH // CK.
Tứ giác AHCK có: AH // CK, AH = CK nên là hình bình hành.
b) Vì AHCK là hình bình hành nên AK // CH, hay AM // CN. (1)
Hơn nữa, ABCD là hình bình hành và N ∈AD, M ∈ BC nên AN // CM. (2)
Từ (1) và (2) suy ra ANCM là hình bình hành.
Vậy AN = CM.
c) Tứ giác AHCK là hình bình hành có hai đường chéo AC, HK cắt nhau tại trung điểm
O của HK nên O cũng là trung điểm của AC.
Tứ giác ANCM là hình bình hành có hai đường chéo AC, NM cắt nhau tại trung điểm
O của AC nên O cũng là trung điểm của MN.
Vậy M, O, N thẳng hàng.
Xem thêm các bài giải sách bài tậpToán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.