Với Giải trang 28 SBT Toán lớp 11 trong Bài tập cuối chương 1 trang 25 Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.
Nội dung bài viết
SBT Toán 11 trang 28 Tập 1 (Kết nối tri thức)
A. S = 2π.
B. S = 0.
C. S = 4π.
D. S = 3π.
Lời giải:
Đáp án đúng là: A
Ta có 3cos x – 1 = 0 ⇔cosx=13⇔cosx≈cos(0,392π)
Mà x ∈ (0; 2π) nên x ≈ 0,392π hoặc x ≈ – 0,392π + 2π.
Vậy tổng các nghiệm cần tìm là S = 0,392π + (– 0,392π + 2π) = 2π.
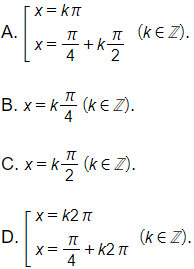
Lời giải:
Đáp án đúng là: A
Giá trị của hai hàm số y = sin3x và y = sin x bằng nhau khi và chỉ khi sin 3x = sin x
B. TỰ LUẬN
a) 23π4; b) 31π6; c) – 1 380°.
Lời giải:
a) Ta có 23π4=6π−π4. Góc 23π4 được biểu diễn bởi điểm M(√22; −√22) trên đường tròn lượng giác (hình dưới).
Vậy sin23π4=−√22; cos23π4=√22 và tan23π4=cot23π4=−1.
b) Ta có 31π6=7π6+4π. Góс 31π6 được biểu diễn bởi điểm M(−√32; −12)> trên đường tròn lượng giác (hình dưới).
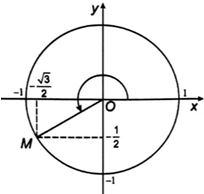
Vậy sin31π6=−12; cos31π6=−√32; tan31π6=1√3 và cot31π6=√3.
c) Ta có – 1 380° = − 4 . 360° + 60°. Góc –1 380° được biểu diễn bởi điểm M(12; √32) trên đường tròn lượng giác (hình dưới).

Vậy sin(– 1 380°) = √32; cos(– 1 380°) = 12; tan(– 1 380°) = √3 và cot(– 1 380°) = 1√3.
Lời giải:
+) Trong 15 phút thì mũi kim phút vạch nên một cung tròn có độ dài bằng 14 độ dài đường tròn, do đó độ dài của cung này bằng
14⋅2π⋅R=14⋅2π⋅1,75=7π8≈2,75 (m).
+) Trong 15 phút thì mũi kim giờ vạch nên một cung tròn có độ dài bằng 14⋅112=148 đường tròn, do đó độ dài của cung này bằng
148⋅2π⋅R'.
Lời giải:
Góc ở tâm chắn cung kinh tuyến nối huyện Quản Bạ tỉnh Hà Giang và huyện Cái Nước tỉnh Cà Mau có số đo bằng 23° – 9° = 14°.
Vậy độ dài cung kinh tuyến đó bằng .
Ta có cos 2α = 2 cos2 α – 1 = .
Ta có sin2 α = 1 – cos2 a = = .
Lại do sin α > 0 nên sin α = .
Suy ra sin 2α = 2 sin α cos α = .
Ta có cos 2β = 1 – 2 sin2 β = = .
Ta có cos2 β = 1 – sin2 β = = .
Lại do nên cos β < 0, do đó .
Suy ra sin 2β = 2 sin β cos β = .
Ta có
cos(α + β) = cos α cos β – sin α sin β = .
sin(α – β) = sin α cos β – cos α sin β = .
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau
b) ;
c) ;
d) .
Lời giải:
a)
.
b)
.
c)
.
d)
.
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x:
a) ;
b) ;
c) ;
d) .
Lời giải:
a) Cách 1:
.
Vậy biểu thức A không phụ thuộc vào biến x.
Cách 2:
.
Vậy biểu thức A không phụ thuộc vào biến x.
b)
.
Vậy biểu thức B không phụ thuộc vào biến x.
c)
.
Vậy biểu thức C không phụ thuộc vào biến x.
d)
.
Vậy biểu thức D không phụ thuộc vào biến x.
Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 1.31 trang 25 SBT Toán 11 Tập 1: Đổi số đo góc α = 105° sang rađian ta được
Bài 1.33 trang 25 SBT Toán 11 Tập 1: Giá trị Cot 89 pi/6 bằng bao nhiêu
Bài 1.34 trang 25 SBT Toán 11 Tập 1: Cho pi/2 < a < pi. Mệnh đề nào sau đây đúng
Bài 1.35 trang 25 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
Bài 1.36 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào đúng?
Bài 1.37 trang 26 SBT Toán 11 Tập 1: Biết sin x = 1/2. Giá trị của cos2 x bằng
Bài 1.39 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
Bài 1.40 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
Bài 1.41 trang 26 SBT Toán 11 Tập 1: Tập xác định của hàm số y = căn 1 - cosx là
Bài 1.42 trang 26 SBT Toán 11 Tập 1: Khẳng định nào sau đây đúng?
Bài 1.43 trang 27 SBT Toán 11 Tập 1: Khẳng định nào sau đây sai?
Bài 1.44 trang 27 SBT Toán 11 Tập 1: Hàm số nào dưới đây có đồ thị nhận trục tung làm trục đối xứng?
Bài 1.45 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
Bài 1.46 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
Bài 1.47 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào dưới đây đúng?
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình 2cosx= căn 3 trên đoạn 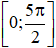 là
là
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x
Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau: a)
Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p: a) y = sin x – cos x
Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau: a) y = sin3 x – cot x
Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau: a) y = sin + cos 3x
Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau: a)
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau: a) sin 5x + cos 5x = – 1
Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.