Với Giải trang 30 SBT Toán lớp 11 trong Bài tập cuối chương 1 trang 25 Sách bài tập Toán lớp 11 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán lớp 11.
SBT Toán 11 trang 30 Tập 1 (Kết nối tri thức)
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau:
b) cos 3x – cos 5x = sin x;
c) 2 cos2 x + cos 2x = 2;
d) sin4 x + cos4 x = sin2 2x.
Lời giải:
a) Ta có sin 5x + cos 5x = – 1
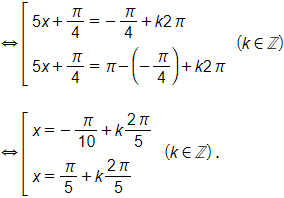
b) Ta có cos 3x – cos 5x = sin x
+ Với sin x = 0 ta được x = kπ (k ∈ ℤ).
+ Với
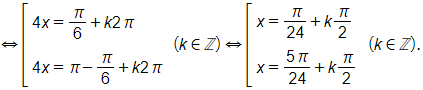
c) Ta có 2 cos2 x + cos 2x = 2
⇔ (2 cos2 x – 1) + cos 2x = 1
⇔ cos 2x + cos 2x = 1
⇔ 2cos 2x = 1
⇔ cos 2x =
⇔ cos 2x =
⇔ 2x =
.
d) Ta có sin4 x + cos4 x = sin2 2x
(do sin2 2x + cos2 2x = 1)
.
a) Chứng minh rằng diện tích mặt cắt của thanh xà gồ được tính bởi công thức
S(θ) = 450 sin 2θ (cm2),
ở đó góc θ được chỉ ra trong hình vẽ dưới đây.
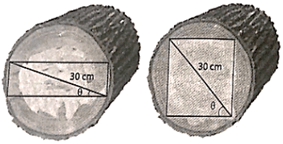
b) Tìm góc θ để diện tích mặt cắt của thanh xà gồ là lớn nhất.
Lời giải:
a) Mặt cắt của thanh xà gồ (hình dưới) là hình chữ nhật có hai kích thước là
AB = 30cos θ và BC = 30sin θ.
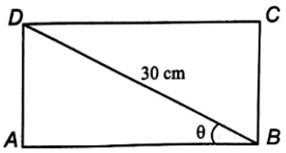
Vậy diện tích mặt cắt là S = AB ∙ BC = 30cos θ ∙ 30sin θ = 450sin 2θ.
b) Vì – 1 ≤ sin 2θ ≤ 1 nên ta có S = 450sin 2θ ≤ 450.
Vậy diện tích mặt cắt của thanh xà gồ lớn nhất khi sin 2θ = 1 hay góc θ = 45°.
ở đó P(t) là huyết áp tính theo đơn vị mmHg (milimét thuỷ ngân) và thời gian t tính theo giây.
a) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 100 mmHg.
b) Trong khoảng từ 0 đến 1 giây, hãy xác định số lần huyết áp là 120 mmHg
Lời giải:
a) Huyết áp là 100 mmHg khi
.
Xét 0 < t < 1 . Suy ra k ∈ {1; 2} vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 2 lần huyết áp là 100 mmHg.
b) Huyết áp là 120 mmHg khi
.
Xét 0 < t < 1 . Suy ra k = 0 vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 1 lần huyết áp là 120 mmHg.
a) Huyết áp là 100 mmHg khi
.
Xét 0 < t < 1 . Suy ra k ∈ {1; 2} vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 2 lần huyết áp là 100 mmHg.
b) Huyết áp là 120 mmHg khi
.
Xét 0 < t < 1 . Suy ra k = 0 vì k ∈ ℤ.
Vậy trong khoảng từ 0 đến 1 giây, có 1 lần huyết áp là 120 mmHg.
Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
Bài 1.31 trang 25 SBT Toán 11 Tập 1: Đổi số đo góc α = 105° sang rađian ta được
Bài 1.33 trang 25 SBT Toán 11 Tập 1: Giá trị Cot 89 pi/6 bằng bao nhiêu
Bài 1.34 trang 25 SBT Toán 11 Tập 1: Cho pi/2 < a < pi. Mệnh đề nào sau đây đúng
Bài 1.35 trang 25 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
Bài 1.36 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào đúng?
Bài 1.37 trang 26 SBT Toán 11 Tập 1: Biết sin x = 1/2. Giá trị của cos2 x bằng
Bài 1.39 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
Bài 1.40 trang 26 SBT Toán 11 Tập 1: Trong các đẳng thức sau, đẳng thức nào sai?
Bài 1.41 trang 26 SBT Toán 11 Tập 1: Tập xác định của hàm số y = căn 1 - cosx là
Bài 1.42 trang 26 SBT Toán 11 Tập 1: Khẳng định nào sau đây đúng?
Bài 1.43 trang 27 SBT Toán 11 Tập 1: Khẳng định nào sau đây sai?
Bài 1.44 trang 27 SBT Toán 11 Tập 1: Hàm số nào dưới đây có đồ thị nhận trục tung làm trục đối xứng?
Bài 1.45 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
Bài 1.46 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào sau đây sai?
Bài 1.47 trang 27 SBT Toán 11 Tập 1: Mệnh đề nào dưới đây đúng?
Bài 1.48 trang 27 SBT Toán 11 Tập 1: Số nghiệm của phương trình 2cosx= căn 3 trên đoạn 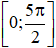 là
là
Bài 1.55 trang 28 SBT Toán 11 Tập 1: Rút gọn các biểu thức sau
Bài 1.56 trang 28 SBT Toán 11 Tập 1: Chứng minh các biểu thức sau không phụ thuộc vào x
Bài 1.58 trang 29 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau: a)
Bài 1.59 trang 29 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của p: a) y = sin x – cos x
Bài 1.60 trang 29 SBT Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau: a) y = sin3 x – cot x
Bài 1.61 trang 29 SBT Toán 11 Tập 1: Xét tính tuần hoàn của các hàm số sau: a) y = sin + cos 3x
Bài 1.62 trang 29 SBT Toán 11 Tập 1: Giải các phương trình sau: a)
Bài 1.63 trang 30 SBT Toán 11 Tập 1: Giải các phương trình sau: a) sin 5x + cos 5x = – 1
Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.