Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Câu 1: Hàm đa thức bậc ba có thể có mấy cực trị?

A. 1

B. 2

C. 0

D. B và C đều đúng

Lời giải:

$y^{\prime }=0$ có hai nghiệm phân biệt $x_1,x_2\Rightarrow$ có $2$ cực trị.

$y^{\prime }=0$ vô nghiệm hoặc có nghiệm kép $\Rightarrow$ không có cực trị.

Do đó hàm đa thức bậc ba chỉ có thể có $2$ cực trị hoặc không có cực trị nào.

Đáp án cần chọn là: D

Câu 2: Số điểm cực trị của hàm số $y=a{x}^3+b{x}^2+cx+d\left(a\ne 0\right)$ có thể có nhiều nhất mấy điểm cực trị?

A. 3

B. 2

C. 1

D. 0

Lời giải:

Hàm đa thức bậc ba chỉ có thể có 2 cực trị hoặc không có cực trị nào nên số điểm cực trị nhiều nhất có thể có là 

Đáp án cần chọn là: B

Lời giải:

Hàm đa thức bậc ba không có cực trị và nghịch biến thì đạo hàm $y^{\prime }$ mang dấu âm với mọi $x\in \left(-\mathrm{\infty };+\mathrm{\infty }\right)$.

Đáp án cần chọn là: B

Lời giải:

- Hàm số bậc ba không có cực trị thì nó đơn điệu tăng hoặc giảm trên $R$ nên đồ thị luôn cắt trục hoành tại $1$ điểm duy nhất nên A đúng, D sai.

- Hàm số bậc ba có 2 cực trị thì đồ thị có thể cắt trục hoành tại $1,2$ hoặc $3$ điểm nên B, C sai.

Đáp án cần chọn là: A

Lời giải:

- Hàm số bậc ba có 2 điểm cực trị thì đồ thị có thể cắt trục hoành tại $1,2$ hoặc 3 điểm nên C, D sai.

- Đồ thị hàm số bậc ba cắt trục hoành tại $1$ điểm duy nhất thì nó có thể có $2$ điểm cực trị hoặc không có điểm cực trị nào.

Đáp án cần chọn là: B

Lời giải:

Hàm số bậc ba luôn có $y_{CD}>y_{CT}$ nên nếu $y_{CD}=0$ thì $y_{CT}<0$.

Do đó điểm cực tiểu của đồ thị hàm số luôn nằm dưới trục hoành.

Đáp án cần chọn là: D

Lời giải:

Từ các dạng đồ thị trên ta thấy hai đồ thị đều có 2 điểm chung với trục hoành.

Đáp án cần chọn là:C

Lời giải:

Quan sát các dáng đồ thị của hàm số bậc ba:

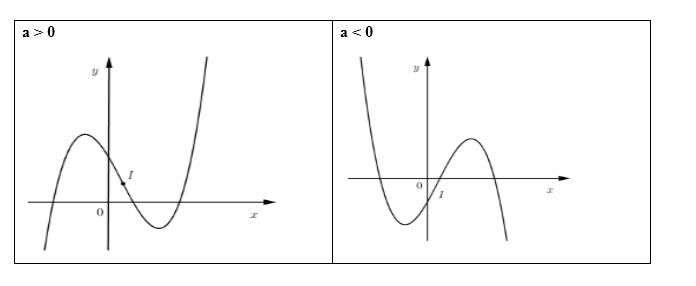
Ta thấy đồ thị hàm số bậc ba chỉ có $2$ điểm chung với trục hoành nếu một trong hai điểm cực trị của đồ thị hàm số nằm trên trục hoành hay một trong hai điểm cực trị của hàm số là nghiệm của phương trình $f\left(x\right)=0$

Đáp án cần chọn là: D

Lời giải:

Hàm số có $2$ cực trị thì có bảng biến thiên ở các dạng sau:

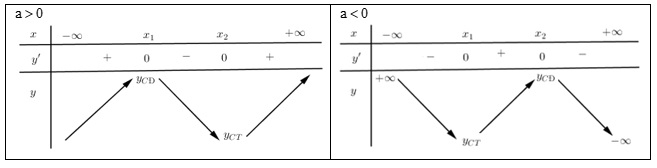
Quan sát bảng biến thiên ta thấy:

Nếu $y_{CD}.y_{CT}<0$ thì $y_{CT}<0<y_{CD}$ nên đường thẳng $y=0$ cắt đồ thị hàm số tại $3$ điểm phân biệt.

Đáp án cần chọn là:A

Lời giải:

Vì $y_{CD}.y_{CT}=0\iff [\begin{array}{l}{y}_{CD}=0\\ y_{CT}=0\end{array}$ hay một trong hai điểm cực trị của đồ thị hàm số nằm trên trục hoành.

Khi đó đồ thị hàm số chỉ có $2$ giao điểm chung với $Ox$

Đáp án cần chọn là: B

Lời giải:

Đáp án A: Hàm số bậc ba có $2$ cực trị thì đồ thị hàm số cắt trục hoành tại $3$ điểm phân biệt nếu $y_{CD}.y_{CT}<0$ hoặc chỉ cắt $Ox$ tại 1 điểm nếu $y_{CD}.y_{CT}>0$ nên A sai.

Đáp án B: Đồ thị hàm số bậc ba luôn cắt trục hoành tại ít nhất $1$ điểm nhưng chưa chắc đó là điểm uốn nên B sai.

Đáp án C: Đồ thị hàm số bậc ba cắt trục hoành tại $3$ điểm phân biệt thì hàm số có hai điểm cực trị là đúng.

Đáp án D: Đồ thị hàm số bậc ba cắt trục hoành tại $1$ điểm duy nhất thì nó không có cực trị hoặc có cực trị nhưng hai giá trị cực trị cùng dấu nên D sai.

Đáp án cần chọn là:C

Lời giải:

Đáp án A: Đồ thị hàm số bậc ba luôn có điểm uốn nhưng chưa chắc thuộc trục tung nên A sai.

Đáp án B: Đồ thị hàm số bậc ba không có trục đối xứng nên B sai.

Đáp án C: Điểm uốn chính là tâm đối xứng của đồ thị hàm số bậc ba nên với mỗi điểm thuộc đồ thị, lấy đối xứng qua điểm đó ta cũng được một điểm thuộc đồ thị nên C đúng.

Đáp án D: Đồ thị hàm số bậc ba $y=a{x}^3+b{x}^2+cx+d\left(a\ne 0\right)$ luôn chỉ có một điểm chung duy nhất với $Oy$ nên D sai.

Đáp án cần chọn là: C

Lời giải:

Hàm bậc bốn trùng phương có $a>0$ và $3$ điểm cực trị thì có $1$ điểm cực đại và $2$ điểm cực tiểu.

Đáp án cần chọn là:A

Lời giải:

Hàm số bậc bốn trùng phương luôn có ít nhất $1$ điểm cực trị.

Đáp án cần chọn là: D

Lời giải:

Đồ thị hàm bậc 4 trùng phương luôn cắt trục tung tại điểm $\left(0;c\right)$ chính là cực trị của đồ thị hàm số.

Ngoài ra, đồ thị hàm số bậc 4 trùng phương cũng có thể không cắt $Ox$ nên A sai.

Đồ thị nhận trục tung làm trục đối xứng chứ không phải trục hoành nên C sai.

Đồ thị không có tâm đối xứng nên D sai.

Đáp án cần chọn là:B

Lời giải:

Đồ thị hàm bậc 4 trùng phương luôn cắt trục tung tại điểm $\left(0;c\right)$ chính là cực trị của đồ thị hàm số.

Ngoài ra, đồ thị hàm số bậc 4 trùng phương cũng có thể không cắt $Ox$ nên A sai.

Đồ thị nhận trục tung làm trục đối xứng nên C sai.

Đồ thị không có tâm đối xứng nên D sai.

Đáp án cần chọn là: B

Lời giải:

Hàm số $y=a{x}^4+b{x}^2+c$ có $a<0,b>0$ nên có $3$ cực trị và đồ thị có dạng như sau:

Quan sát đồ thị ta thấy:

- Hàm số có $2$ cực đại và $1$ cực tiểu nên A đúng.

- Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành nếu $y_{CD}<0$ nên B đúng.

- Đồ thị hàm số cắt $Ox$ tại hai điểm phân biệt nếu $c>0$ nên C đúng, D sai.

Đáp án cần chọn là:D

Lời giải:

Ta có: $y={\displaystyle \frac{x-3}{2x-6}}={\displaystyle \frac{1}{2}},\mathrm{\forall }x\ne 3$

Do đó đồ thị hàm số không có tiệm cận đứng.

Đáp án cần chọn là: B

Lời giải:

+ Đáp án A : Xét phương trình hoành độ giao điểm $\frac{2x-1}{x+1}=0\Rightarrow x=\frac{1}{2}$ nên đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x=\frac{1}{2}$. Do đó A đúng.

+ Đáp án B: Đồ thị số có tiệm cận ngang là: $y=\frac{2}{1}=2$. Do đó B đúng.

+ Đáp án C: Hàm số $y=\frac{2x-1}{x+1}$ có ĐK: $x\ne -1$ nên nó gián đoạn tại $x=-1$ nên C đúng.

+ Đáp án D: Hàm số $y=\frac{2x-1}{x+1}$ có $y^{\prime }=\frac{3}{{\left(x+1\right)}^2}>0;\mathrm{\forall }x\ne -1$ nên nó đồng biến trên từng khoảng xác định $\left(-\mathrm{\infty };-1\right);\left(-1;+\mathrm{\infty }\right)$. Do đó D sai vì ta không thể nói đồng biến trên tập xác định của hàm số.

Đáp án cần chọn là:D

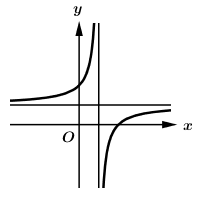
Lời giải:

+ Từ đồ thị ta nhận thấy hàm số đồng biến trên mỗi khoảng xác định $\Rightarrow y^{\prime }>0$.

+ Do hàm số $y={\displaystyle \frac{x+a}{x-1}}$ không xác định tại $x=1$ $\Rightarrow y^{\prime }>0\mathrm{\forall }x\ne 1$.

Đáp án cần chọn là: A

Câu 21: Đường cong trong hình dưới đây là đồ thị của một hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x⁴ + 3x² - 2

B. y = x³ - 2x² + 1

C. y = -4x⁴ + x² + 4

D. y = x⁴ - 2x² + 3

Lời giải:

Dựa vào hình vẽ, ta thấy đây là đồ thị ứng với hàm bậc bốn trùng phương có a > 0 và a, b, trái dấu.

Đáp án cần chọn là:D

Câu 22: Đồ thị trong hình dưới đây là đồ thị của đồ thị hàm số nào?

A. y = x² - 2x + 1

B. y = x³ + 4x² - 2x + 5

C. y = x⁴ + x² + 1

D. y = x⁴ - 3x² + 5

Lời giải:

Dựa vào hình vẽ, ta thấy đồ thị trên là của hàm trùng phương có a > 0 và a, b, cùng dấu hoặc hàm số bậc hai với a > 0 ⇒ loại B và D.

Tuy nhiên đỉnh của parabol của đồ thị hàm số y = -x³ - 3x² + 1 là I(1; 0) nằm trên trục hoành ⇒ loại A

Đáp án cần chọn là: C

Câu 23: Tâm đối xứng của đồ thị hàm số y = -x³ - 3x² + 1 là:

A. (-1; -1)

B. (-2; -3)

C. (0; 1)

D. Không có đáp án

Lời giải:

y' = -3x² - 6x; y'' = -6x - 6; y'' = 0 => x = -1

Vậy điểm U(-1; -1) là tâm đối xứng của đồ thị .

(Đồ thị hàm số bậc ba nhận điểm uốn làm tâm đối xứng – hoành độ điểm uốn là nghiệm phương trình y'' = 0 ).

Đáp án cần chọn là:A

Câu 24: Trong các mệnh đề sau, mệnh đề nào đúng?

A. I(1; 0) là tâm đối xứng của

B. I(1; 0) là tâm đối xứng của y = -x³ + 3x² - 2

C. I(1; 0) là điểm thuộc đồ thị

D. I(1; 0) là giao điểm của y = x³ - 3x² - 2 với trục hoành.

Lời giải:

Đối với hàm phân thức hữu tỉ, giao điểm của 2 đường tiệm cận là tâm đối xứng của đồ thị hàm số.

A. Tâm đối xứng của

C. Điểm I(1; 0) không thuộc đồ thị

D. Điểm I(1; 0) không thuộc đồ thị y = x³ - 3x² - 2 nên không phải là giao điểm của y = x³ - 3x² - 2 với trục hoành.

Đáp án cần chọn là: B

Câu 25: Tìm m để bất phương trình x⁴ + 2x² ≥ m luôn đúng.

A. m = 0

B. m < 0

C. m ≤ 0

D. Không có đáp án

Lời giải:

Xét hàm số y = x⁴ + 2x² có a = 1 > 0; b = 2 > 0 => a, b cùng dấu.

Đồ thị có dạng như hình bên.

Do đó, để bất phương trình x⁴ + 2x² ≥ m luôn đúng thì m ≤ min(x⁴ + 2x²)

Từ đồ thị hàm số ta suy ra m ≤ 0 .

Đáp án cần chọn là:C

Câu 26: Cho hàm số

Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x -1

A. y = 3x + 1

B. y = 3x - 29/3

C. 3x + 20

D. Cả A và B đúng

Lời giải:

Ta có y' = x² - 4x + 3. Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.

Xét y' = 3 <=> x² - 4x = 0

Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1

Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là

Đáp án cần chọn là: D

Câu 27: Gọi M, N là giao điểm của

Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng

A. 2

B. 1

C. 0

D. -1

Lời giải:

Xét phương trình hoành độ giao điểm

Giao điểm của hai đồ thị hàm số là M(x₁; y₁), N(x₂; y₂) với x₁, x₂ là nghiệm phương trình (1). Do đó

Đáp án cần chọn là:B

Câu 28: Tìm m để phương trình x³ + 3x² = m có ba nghiệm phân biệt

A. m > 4

B. m < 0

C. 0 ≤ m ≤ 4

D. 0 < m < 4

Lời giải:

Xét hàm số y = f(x) = x³ + 3x² (C)

Đồ thị hàm số có dạng như hình bên.

x³ + 3x² = m có ba nghiệm phân biệt

<=> Đường thẳng y = m cắt đồ thị (C) tại ba điểm phân biệt <=> 0 < m < 4

Đáp án cần chọn là: D

Câu 29: Cho hàm số y = 3x - 4x³ . Có nhiều nhất mấy tiếp tuyến với đồ thị hàm số đi qua điểm M(1; 3) ?

A. 1

B. 2

C. 3

D. 4

Lời giải:

y' = 3 - 12x

Đường thẳng (d) có hệ số góc là k đi qua M(1;3) y=k(x-1)+3 .

Đường thẳng (d) tiếp xúc với đồ thì hàm số khi hệ phương trình sau có nghiệm

Với x = 0 thì k = 3

Do đó có tối đa hai tiếp tuyến đi qua điểm M(1;3).

Đáp án cần chọn là:B

Câu 30: Với m > 0 phương trình 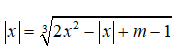có ít nhất mấy nghiệm?

A. 0

B. 1

C. 2

D.3

Lời giải:

Đồ thị hàm số y = |x|³ - 2x² + |x| + 1 có dạng như hình (2)

Số nghiệm của phương trình |x|³ - 2x² + |x| + 1 = m là số giao điểm của đồ thị hàm số y = |x|³ - 2x² + |x| + 1 và đường thẳng y = m.

Số nghiệm của phương trình |x|³ - 2x² + là số giao điểm của đồ thị hàm số và đường thẳng y = m.

Dựa vào đồ thị với m > 0 phương trình có tối thiểu 0 nghiệm ( 0 nghiệm – tức là phương trình vô nghiệm).

Đáp án cần chọn là: A

Lời giải:

Xét phương trình hoành độ giao điểm $\left(x-2\right)\left(x^2+1\right)=0\iff x-2=0\iff x=2$ (do $x^2+1>0\mathrm{\forall }x$).

Vậy $\left(C\right)$ cắt trục hoành tại một điểm.

Đáp án cần chọn là:A

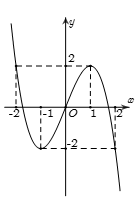
Lời giải:

Đáp án A: đúng.

Đáp án B: Với $m>2$ hoặc $m<-2$ thì đường thẳng $y=m$ cắt đồ thị hàm số tại một điểm duy nhất nên B đúng.

Đáp án C: Hàm số đạt cực tiểu tại $x=-1$ chứ không phải đạt cực tiểu bằng $-1$ nên C sai.

Đáp án D: Giá trị lớn nhất của hàm số trên $\left[-2;2\right]$ đạt được bằng $2$ tại $x=-2$ nên D đúng.

Đáp án cần chọn là: C

Câu 33. Tiếp tuyến của đồ thị hàm số 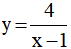 tại điểm có hoành độ x₀ = 2 có phương trình là:

A. y = -2x - 2

B. y = -4x + 12

C. y = x -1

D. y = -2x + 2

Lời giải:

Tập xác định: D = R\ {1}.

Đạo hàm : 

Suy ra: y’(2) = - 4 và y(2) = 4.

Do đó phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x₀ = 2 là:

y = -4(x – 2) + 4 hay y = - 4x+ 12

Đáp án cần chọn là:B

Câu 34. Cho hàm số y = x³ + x²- 6x+ 1. Phương trình tiếp tuyến tại điểm A(0; 1)

A. y = -2x+ 1

B. y = 2x+ 1

C. y = - 6x+ 1

D.y = 3x+ 1

Lời giải:

Hàm số đã cho liên tục và xác định trên R.

Đạo hàm: y’ = 3x² + 2x- 6

Ta có: y’(0) = - 6 nên phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm A(0; 1) là:

y = - 6(x- 0) + 1 hay y = - 6x + 1

Đáp án cần chọn là: C

Câu 35. Cho hàm số y = 2x² + 4x+ 1. Tiếp tuyến của đồ thị hàm số tại điểm có tung độ -1 có phương trình là

A. y = x+ 1

B.y = x

C. y = 1

D. y = -1

Lời giải:

Hàm số đã cho liên tục và xác định trên R .

Đạo hàm: y’ = 4x+ 4.

Với y = -1 ta có: 2x² + 4x+ 1 = - 1 ⇔ x = -1. Bài toán trở thành viết phương trình tiếp tuyến tại điểm A(- 1; -1)

Ta có y’(-1) = 0. Do đó, phương trình tiếp tuyến cần tìm là:

y = 0 (x+1) – 1 hay y = - 1

Đáp án cần chọn là:D

Câu 36. Cho đồ thị (C) của hàm số y = x³ + 6x² – 12x+ 1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm uốn.

A. y = - 24 x- 7

B. y = 10 x+ 2

C. y = 24 x + 1

D. Đáp án khác

Lời giải:

Hàm số đã cho liên tục và xác định trên R.

Ta có: y’ = 3x² + 12x – 12 và y” = 6x+ 12.

Xét phương trình: y” = 0 ⇔ x = - 2 ⇒ y (-2) = 41 và y’(-2) = - 24.

Do đó điểm uốn của đồ thị hàm số là I(- 2; 41). Phương trình tiếp tuyến tại điểm uốn là :

y = - 24(x+ 2) + 41 hay y = -24x – 7

Đáp án cần chọn là: A

Câu 37. Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số 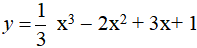 có phương trình là:

A. y = 1 

B. y = 0

C. y = x+ 1

D. y = x - 1

Lời giải:

+ Hàm số đã cho xác định và liên tục trên R.

+ Đạo hàm y’ = x² - 4x + 3.

Do đó, hàm số đạt cực tiểu tại điểm x = 3.

+ ta viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = 3.

Ta có: (3) = 1 và y’(3) = 0.

Do đó phương trình tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là :

y = 0. (x- 3) +1 hay y = 1.

Đáp án cần chọn là:A

Câu 38. Cho hàm số 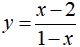 có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:

A. y = - x + 1

B. y = - x+ 2

C. y = - 2x + 4

D. y = x - 2

Lời giải:

Trực hoành có phương trình là y = 0.

Phương trình giao điểm của (H) và trục hoành là:

 ⇒ y(2) = 0.

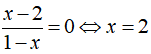
Vậy giao điểm của đồ thị hàm số (H) và trục hoành là I(2; 0)

Đạo hàm: 

Phương trình tiếp tuyến tại giao điểm I của ( H) và trục hoành là:

y = -1. (x- 2) + 0 hay y = - x + 2.

Đáp án cần chọn là: B

Câu 39. Hệ số góc của tiếp tuyến của đồ thì hàm số 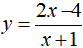 tại giao điểm của đồ thị hàm số với trục tung bằng.

A. -2

B. 2

C. 6

D. 3

Lời giải:

Tập xác định: D = R\ {- 1}.

Điểm A(x; y) là giao điểm của đồ thị hàm số và trục tung thỏa mãn hệ phương trình:

Suy ra; hệ số góc của tiếp tuyến của đồ thị hàm số đã cho tại giao điểm của đồ thị hàm số với trục tung là k = y’(0) = 6

Đáp án cần chọn là:C

Câu 40. Hệ số góc của tiếp tuyến của đồ thị hàm số 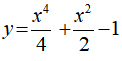 tại điểm có hoành độ x₀ = 1 bằng:

A. -2

B. 2

C. 0

D. Đáp số khác

Lời giải:

Đạo hàm y’ = x³ + x.

Ta có y(1) = 2 và y’(1) = 2.

Do đó, hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1 là:

k = y’(1) = 2

Đáp án cần chọn là: B

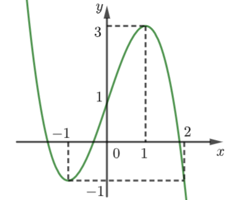
Lời giải:

Ta có: $f\left(f\left(x\right)\right)=1\iff [\begin{array}{l}f\left(x\right)=a\left(a<-1\right)\\ f\left(x\right)=0\\ f\left(x\right)=b\left(1<b<2\right)\end{array}$

Dựa vào đồ thị ta thấy: $f\left(x\right)=a$ với $a<-1$ có $1$ nghiệm.

$f\left(x\right)=0$ có $3$ nghiệm.

$f\left(x\right)=b$ với $1<b<2$ có $3$ nghiệm

Số nghiệm thực phân biệt của phương trình $f\left(f\left(x\right)\right)=1$ là $7$

Đáp án cần chọn là:B

Câu 42: Hàm số y = f(x) liên tục trên R và có bảng biến thiên dưới đây. Khẳng định nào sau đây là đúng?

A. Hàm số có ba điểm cực trị.

B. Hàm số đạt cực đại tại x = 0.

C. Hàm số đạt cực tiểu tại x = -1.

D. Hàm số đạt cực đại tại x = 2.

Lời giải:

Chọn đáp án: C

Đáp án cần chọn là: C

Câu 43: Cho hàm số y = f(x) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là khẳng định sai?

A. Hàm số nghịch biến trên R

B. Hàm số đạt cực tiểu tại x = 1

C. Hàm số không có cực trị.

D. 

Lời giải:

Từ bảng biến thiên của hàm số ta thấy hàm số nghịch biến trên R, hàm số không có cực trị và

Vậy khẳng định sai là “Hàm số đạt cực tiểu tại x = 1”

Đáp án cần chọn là:B

Câu 44: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.

Khẳng định nào sau đây là sai?

A. M(0; 2) được gọi là điểm cực đại của hàm số.

B. f(-1) được gọi là giá trị cực tiểu của hàm số.

C. x₀ = 1 được gọi là điểm cực tiểu của hàm số.

D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞).

Lời giải:

Điểm M(0; 2) được gọi là điểm cực đại của đồ thị hàm số.

Đáp án cần chọn là:A

Câu 45: Đường tiệm cận ngang của hàm số y = (x-3)/(2x+1) là

A. x = 1/2.

B. x = -1/2.

C. y = -1/2.

D. y = 1/2.

Lời giải:

Ta có: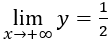 nên TCN là y = 1/2.

Đáp án cần chọn là:D

Câu 46: Cho hàm số y = (2x-1)/(x+1). Khẳng định nào sau đây đúng?

A. Đồ thị có tiệm cận đứng x = -1.

B. Đồ thị có tiệm cận ngang y = 1

C. Đồ thị có tiệm cận đứng x = 1.

D. Đồ thị có tiệm cận ngang y = 3

Lời giải:

Ta có: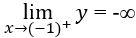 nên đường thẳng x = -1 là tiệm cận đứng của đồ thị.

Đáp án cần chọn là:A

Câu 47: Đồ thị hàm số y = (1-2x)/(x-1) có tiệm cận đứng là đường thẳng nào sau đây?

A. x = -2.

B. y = -2.

C. y = 1.

D. x = 1.

Lời giải:

Ta có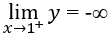 nên đồ thị hàm số có tiệm cận đứng là x = 1.

Đáp án cần chọn là:D

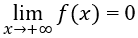
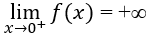
Câu 48: Cho hàm số y = f(x) có và . Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận đứng.

B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho.

C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng y = 0.

D. Hàm số đã cho có tập xác định là D = (0; +∞).

Lời giải:

Vì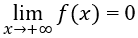 => TCN y = 0 => TCN là trục hoành

Vì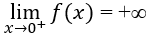 => TCĐ x = 0 => TCĐ là trục tung

Đáp án cần chọn là:B

Câu 49: Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y = (2x+3)/(x+1)?

A. y = 2

B. y = -1

C. x = 1

D. x = -1

Lời giải:

Vì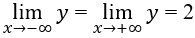 nên đồ thị hàm số có tiệm cận ngang là y = 2.

Đáp án cần chọn là:A

Câu 50: Tìm tiệm cận đứng của đồ thị hàm số y = (2x+1)/(x+1)

A. x = 1

B. y = 2

C. x = -1

D. x = -2

Lời giải:

Vì: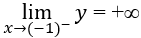 và

Đáp án cần chọn là:C