Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Phương trình mũ và phương trình lôgarit (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Phương trình mũ và phương trình lôgarit

Câu 1. Phương trình 3^x+1 = 27 có bao nhiêu nghiệm nguyên âm?

A. 0

B. 1

C. 2

D.3

Lời giải:

Ta có: 3^{x + 1} = 27 3^{x + 1} = 3³

⇔x + 1 = 3 ⇔ x = 2

Vậy nghiệm của phương trình đã cho là x = 2. Do đó, phương trình đã cho không có nghiệm nguyên âm.

Đáp án cần chọn là:A

Câu 2. Phương trình 5^x = 10 có nghiệm x = 1+ log₅a. Tìm a?

A. a = 1

B.a = 2

C.a = 5

D.a = 10

Lời giải:

Ta có: 5^x = 10, lấy loga cơ số 5 hai vế ta được:

⇔x = log₅10 = 1 + log₅2

Vậy a= 2.

Đáp án cần chọn là:B

Câu 3. Giải phương trình 4^{2x + 1} = 12.

A. x = log₄3

B. x = log₂3

C. x = log₁₆3

D. x = log₈3

Lời giải:

Ta có: 4^{2x+ 1} = 12, lấy loga cơ số 4 hai vế ta được;

2x + 1= log₄12 ⇔ 2x + 1 = 1 + log₄3

⇔ 2x= log₄3

Đáp án cần chọn là:C

Câu 4. Giải phương trình 2^{x2 − 3x + 6} = 2^{x + 3}

A.x = 1; x = 2

B. x = −1; x = 2

C. x = 1; x = 3

D. x = −1; x = 3

Lời giải:

Phương trình đã cho xác định với mọi x.

Ta có: 2^{x2 − 3x + 6} = 2^{x + 3}

⇔ x² − 3x + 6 = x + 3

⇔ x² − 4x + 3= 0

⇔ x = 1 hoặc x = 3

Đáp án cần chọn là:C

Câu 5. Biết rằng phương trình 2^{x2 − x + 4} = 4^{x + 1} có hai nghiệm phân biệt là x1, x2 ( x1 > x2). Tính giá trị của biểu thức S = x₁⁴ + 2x₂⁴

A. S = 18

B. S = 83

C. S = 21

D. S = 30

Lời giải:

Phương trình đã cho xác định với mọi x.

Ta có: 2^{x2 − x + 4} = 4^{x + 1} ⇔ 2^{x2 − x + 4} = (2²)^{x + 1}

2^{x2 − x + 4} = 2^{2(x + 1)}

x² − x+ 4 = 2( x+ 1) ⇔ x² − 3x + 2 = 0

⇔ x = 1 hoặc x = 2

Do đó, x₁ = 2 và x₂ = 1. Suy ra, S = 24 + 2. 14 = 18

Đáp án cần chọn là:A

Câu 6. Phương trình 2^{8 − x2} . 5^{8 − x2} = 0,001.(10⁵)^{1 − x} có tổng các nghiệm là:

A. 5.

B. 7.

C. − 7

D. −5

Lời giải:

Ta có :

2^{8 − x2} . 5^{8 − x2} = 0,001.(10⁵)^{1 − x}

⇔ (2.5)^{8 − x2} = 10⁻³ . 10^{5 − 5x} ⇔ 10^{8 − x2} = 10^{2 − 5x}

Do đó, tổng các nghiệm của phương trình đã cho là : −1+ 6 = 5.

Đáp án cần chọn là:A

Câu 7. Biết rằng phương trình 9^{x2 − 10x + 11} = 81 có hai nghiệm phân biệt x₁, x₂. Tính S= x₁ + x₂

A. 8

B.10

C. 6

D.12

Lời giải:

Phương trình đã cho xác định với mọi x.

Ta có : 9^{x2 − 10x + 11} = 81 ⇔ (3²)^{x2 − 10x + 11} = 3⁴

⇔(3²)^{x2 − 10x + 11} = 3⁴ ⇔ 2. (x² − 10x + 11) = 4

⇔ 2x² − 20 x + 22 − 4= 0 ⇔ 2x² − 20x + 18 =0

⇔x = 1 hoặc x = 9. Do đó , tổng hai nghiệm của phương trình đã cho là S = 10

Đáp án cần chọn là:B

Câu 8. Cho phương trình : 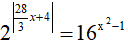. Khẳng định nào sau đây là đúng ?

A. Tích các nghiệm của phương trình là một số âm.

B. Tổng các nghiệm của phương tình là một số nguyên .

C. Nghiệm của phương trình là các số vô tỉ.

D. Phương trình vô nghiệm.

Lời giải:

       

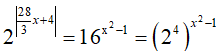
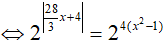
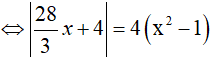
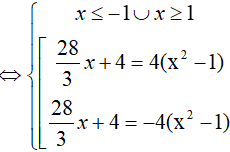
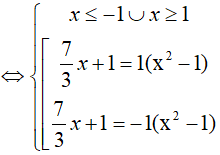
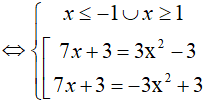
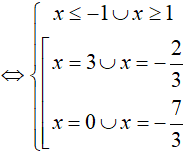
Nghiệm của phương trình là:

Khi đó

Đáp án cần chọn là:A

Câu 9. Phương trình 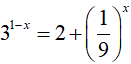 có bao nhiêu nghiệm âm?

A.1.

B. 3.

C. 2.

D. 0.

Lời giải:

Phương trình đã cho xác đinh với mọi x.

Phương trình tương đương với 

Đặt 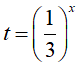(t > 0) . Phương trình trở thành :

3t = 2 + t² ⇔ t² − 3t + 2 = 0 ⇔ t = 1 hoặc t = 2

● Với t= 1, ta được

● Với t= 2, ta được

Vậy phương trình có một nghiệm âm.

Đáp án cần chọn là:A

Câu 10. Số nghiệm của phương trình 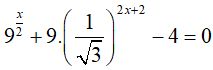là:

A.2

B. 4.

C. 1.

D. 0

Lời giải:

Phương trình đã cho xác định với mọi x.

Phương trình tương đương với 

  

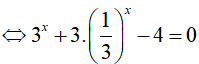
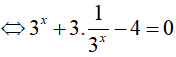
Đặt t = 3x ( t > 0). Phương trình trở thành t² − 4t + 3 = 0 ⇔ t = 1 hoặc t = 3

● Với t = 1, ta được 3^x = 1 ⇔ x = 0.

● Với t = 3, ta được 3^x = 3 ⇔ x = 1.

Vậy phương trình có nghiệm x = 0, x = 1.

Đáp án cần chọn là:A

Câu 11. Cho phương trình 4.4^x − 9. 2^x+1 + 8 = 0 . Gọi x₁; x₂ là hai nghiệm của phương trình trên. Khi đó, tích x₁.x₂ bằng :

A. − 2   

B. 2 

C. − 1

D. 1

Lời giải:

Ta có: 4.4^x − 9. 2^x+1 + 8 =0 ⇔ 4. (2²)^x − 9.2.2^x + 8 = 0

⇔ 4. 2^2x − 18.2^x + 8 = 0

Đặt t= 2^x ( t > 0), khi đó phương trình đã cho tương đương với

4t² − 18t + 8 = 0

 

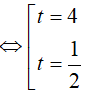
Vậy tích 2 nghiệm phương trình đã cho là: S= 2.(−1)= − 2.

Đáp án cần chọn là:A

Câu 12. Phương trình (7 + 4√3)^x + (2 + √3)^x có nghiệm là:

A. x = log_{(2 + √3)}2

B. x = log₂3

C. x = log₂(2 + √3)

D. x = log₃2

Lời giải:

Ta có: 7 + 4√3 = (2 + √3)²

Do đó, phương trình đã cho trở thành:

(2 + √3)^2x + (2 + √3)^x = 6

Đặt t = (2 + √3)^x( t > 0 ), khi đó phương trình trên tương đương với:

t² + t = 6

⇔ 2 = (2 + √3)^x ⇔ x = log_{(2 + √3)}2

Đáp án cần chọn là:A

Câu 13. Nghiệm của phương trình 12. 3^x + 3. 15^x − 5^{x+ 1} = 20 là:

A. x = log₃5 − 1

B. x = log_>35

C.x = log₃5 + 1.

D. x = log₅3 − 1

Lời giải:

Ta có: 12 . 3^x + 3 . 15^x − 5^{x + 1} = 20

⇔ ( 12.3^x + 3.15^x ) − (5^{x+ 1} + 20) = 0

⇔ 3.3^x ( 4 + 5^x) − 5. ( 5^x +4) = 0

⇔ ( 3.3^x − 5) . (4 + 5^x) = 0

⇔ 3^{x + 1} − 5 = 0 ( vì 4+ 5x > 0 với mọi x)

⇔ 3^x+1 = 5 ⇔ x + 1 = log₃5

⇔ x = log³5 − 1

Đáp án cần chọn là:A

Câu 14. Phương trình sau có tất cả bao nhiêu nghiệm nguyên 4^{x2 − 3x + 2} + 4^{x2 + 6x + 5} = 4^{2x2 + 3x + 7} + 1.

A. 2 

B. 3

C. 4

D.1.

Lời giải:

       

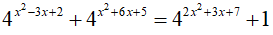
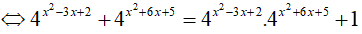
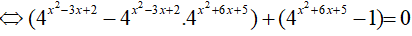
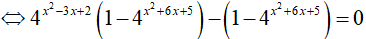
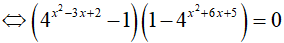
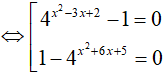
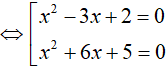
Vậy phương trình đã cho có 4 nghiệm nguyên phân biệt.

Đáp án cần chọn là:A

Câu 15. Phương trình 2^{x − 3} = 3^{x2 − 5x + 6} có bao nhiêu nghiệm không nguyên?

A. 0

B. 1 

C. 2

D. 3.

Lời giải:

Theo đầu bài ta có: 2^{x − 3} = 3^{x2 − 5x + 6}

Logarit hóa hai vế của phương trình (theo cơ số 2) ta được: log₂2^{x − 3} = log₂3^{x2 − 5x + 6}

        

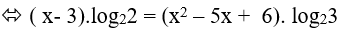
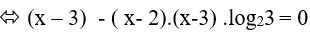
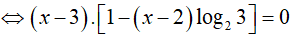
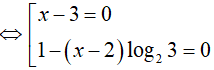
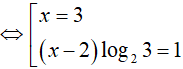
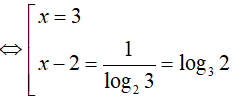
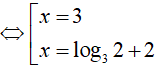
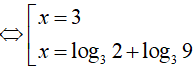
Vậy phương trình đã cho có 1 nghiệm không nguyên

Đáp án cần chọn là:B

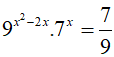
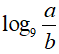
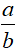
Câu 16. Biết rằng phương trình  có hai nghiệm phân biệt là x₁, x₂ .Tổng x₁ + x₂ có dạng  ,với a,b ∈ N* và  là phân số tối giản. Tính S = a+ 2b

A. S= 95

B. S= 169

C. S= 32

D. S= 43

Lời giải:

Điều kiện: x ∈ R (*)

Phương trình

       

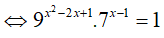
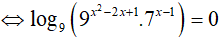
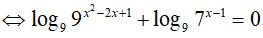
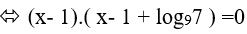
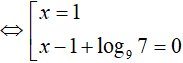
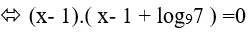
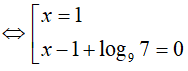
Do đó: x₁ + x₂ = 2 − log₉7 = log₉81 − log₉7

Đáp án cần chọn là:B

Câu 17. Phương trình (√3 − √2)^x + (√3 + √2)^x = (√10)^x có tất cả bao nhiêu nghiệm thực ?

A. 1

B. 2

C. 3

D. 0

Lời giải:

 

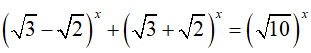
Xét hàm số

Hàm số f(x) nghịch biến trên R do các cơ số

Do đó, nếu phương trình đã cho có nghiệm thì nghiệm đó là duy nhất.

Ta thấy f(2) =1 nên phương trình có nghiệm duy nhất là x = 2.

Đáp án cần chọn là:A

Câu 18. Phương trình 3^2x +2x (3^x + 1) − 4. 3^x − 5 = 0 có tất cả bao nhiêu nghiệm không âm ?

A. 1

B. 2

C. 0

D. 3

Lời giải:

Ta có: 3^2x +2x (3^x + 1) − 4. 3^x − 5 = 0

   

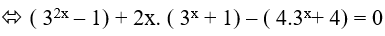
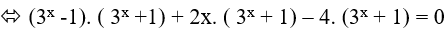
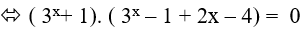
⇔ 3^x + 2x − 5 = 0 ( vì 3^x + 1 > 0 với mọi x)

Xét hàm số f(x) = 3^x + 2x − 5 ; f'(x) = 3^xln3 + 2 > 0; ∀x ∈ R.

Suy ra, hàm số f(x) đồng biến trên R. Do đó, phương trình đã cho nếu có nghiệm thì nghiệm đó là duy nhất.

Lại có, f(1) = 0 nên nghiệm duy nhất của phương trình là x = 1.

Đáp án cần chọn là:A

Câu 19. Phương trình 4^x + 2^x (x − 7) − 4x + 12= 0 có số nghiệm là?

A. 0

B. 1

C. 3

D. 2

Lời giải:

Đặt t= 2x ( t > 0) phương trình đã cho thành: t² + (x − 7)t − 4x + 12= 0 (1)

Coi (1) là phương trình bậc hai ẩn t, ta có

Δ = (x − 7)² − 4(−4x + 12) = x² + 2x + 1 = (x + 1)² ≥ 0

Do đó (1)

+ TH1. Nếu t = 4 thì 2^x = 4 ⇔ x = 2

+ TH2. Nếu t = 3 - x thì 2^x = 3- x , theo ví dụ trên ta được x= 1

Vậy phương trình đã cho có nghiệm là x = 1; x = 2.

Đáp án cần chọn là:D

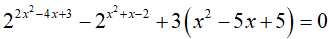
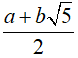
Câu 20. Biết rằng phương trình  có hai nghiệm phân biệt là x₁, x₂ ( x₁ > x₂). Nghiệm x₁ có dạng  , với a,b ∈ Z . Tính S= a⁴ + 10ab

A. S= 11

B. S= − 9

C. S= 575

D. S= 675

Lời giải:

Điều kiện: x ≠ R (*)

Để ý: (2x² − 4x + 3) − (x² + x − 2) = x² − 5x + 5

Ta biến đổi phương trình

⇔ f(2x² − 4x + 3)= f(x² + x − 2) (1)

Xét hàm số f(t) = 2^t + 3t với t ∈ R có f’(t) = 2^t.ln2 + 3 > 0 với mọi t.

Suy ra, hàm số f(t) đồng biến trên R nên (1)

   

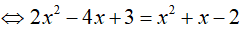
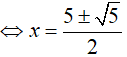
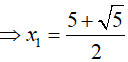
Đáp án cần chọn là:D

Câu 21. Phương trình 2^{x2 + 1} + 3^{x2 + 2} = 5(sinx + cosx) có số nghiệm là ?.

A. 2

B. 1

C. 0

D. 3

Lời giải:

Điều kiện: x ≠ R (*)

Ta có 2^{x2 + 1} + 3^{x2 + 2} ≥ 2^{0 + 1} + 3^{0 + 2} = 11, ∀x ∈ R.

Mà 5(sinx + cosx) ≤ 5(1 + 1) = 10, ∀x ∈ R

=> 2^{x2 + 1} + 3^{x2 + 2} > 5(sinx + cosx) => phương trình vô nghiệm .

Đáp án cần chọn là:C

Câu 22. Với giá trị nào của tham số m thì phương trình (2 + √3)^x + (2 − √3)^x = m vô nghiệm?

A. m ≤ 2

B . m > 2

C. m = 2

D. m < 2

Lời giải:

Nhận xét: (2 + √3) + (2 − √3) = 1 ⇔ (2 + √3)^x + (2 − √3)^x = 1 .

Đặt t = (2 + √3)^x.

Khi đó, phương trình đã cho trở thành:

 

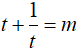
Xét hàm số 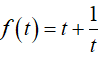 xác định và liên tục trên (0; +∞).

Ta có:

Cho

Bảng biến thiên:

Dựa vào bảng biến thiên, nếu m < 2 thì phương trình (1’) vô nghiệm nên phương trình (1) vô nghiệm.

Đáp án cần chọn là:D

Câu 23. Với giá trị nào của tham số m thì phương trình 4^x − m. 2^x+1 +2m = 0 có hai nghiệm x₁, x₂ thoả mãn x₁ + x₂ = 3?

A. m= − 2

B. m = 4

C. m = 1

D. m = 3

Lời giải:

Ta có: 4^x − m. 2^x+1 +2m = 0 ⇔ (2^x)² − 2m.2^x + 2m = 0 (*)

Phương trình (*) là phương trình bậc hai ẩn 2^x có: Δ' = (−m)² − 2m = m² − 2m

Phương trình (*) có nghiệm ⇔ m² − 2m ≥ 0 ⇔ m(m − 2) ≥ 0

Áp dụng định lý Vi-ét ta có: 2^x₁. 2^x₂ = 2m ⇔ 2^{x₁ + x₂} = 2m

Do đó; x₁ + x₂ = 3 ⇔ 2³ = 2m ⇔ m = 4.

Thử lại ta được m = 4 thỏa mãn.

Đáp án cần chọn là:B

Câu 24. Tìm tập hợp tất cả các giá trị của tham số m để phương trình 6^x +( 3 − m).2^x − m = 0 có nghiệm thuộc khoảng (0; 1)

A. [3; 4]

B. [2; 4]

C. (2; 4)

D. (3; 4)

Lời giải:

Phương trình tương đương: m(2^x + 1) = 6^x + 3 . 2^x.

Xét hàm số

Ta có:

Suy ra, f(x) đồng biến trên khoảng (0 ; 1) thì f(0) < f(x) < f(1)

Đáp án cần chọn là:C

Câu 25.Có bao nhiêu giá trị nguyên của m để phương trình √(3^x + 3)+ √(5 − 3^x) = m có nghiệm.

A. 1

B. 2

C. 3

D. 4

Lời giải:

Điều kiện: 5 − 3^x ≥ 0 ⇔ 3^x ≤ 5 ⇔ x ≤ log₃5

Xét hàm số f(x) = √(3^x + 3) + √(5 − 3^x), x ∈ (−∞; log₃5)

Ta có:

  

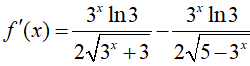
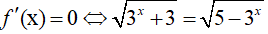
BBT:

Số nghiệm của √(3^x + 3)+ √(5 − 3^x) = m (*) chính là số giao điểm của đồ thị hàm số y= f(x) và đường thẳng y = m

Vậy để (*) có nghiệm thì

Đáp án cần chọn là:B

Câu 26. Điều kiện xác định của phươg trình log_x(2x² − 7x − 12) là:

A. x ∈ (0; 1) ∪ (1: +∞)

B. x ∈ (−∞; 0) .

C. x ∈ (0; 1) .

D. x ∈ (0; +∞)

Lời giải:

Phương trình log_x(2x² − 7x − 12) xác định:

 

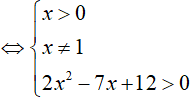
⇔x ∈ (0; 1) ∪ (1: +∞)

Đáp án cần chọn là:A

Câu 27. Điều kiện xác định của phương trình 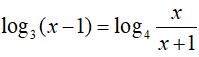 là:

A. x ∈ (1; +∞).

B. x ∈ (−1; 0).

C. x ∈ R\[−1; 0].

D. x ∈ (−∞; 1).

Lời giải:

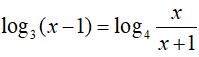
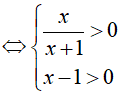
Điều kiện xác định của phương trình đã cho là: Biểu thức log₃(x − 1) và  xác định

 

⇔ x > 1

Đáp án cần chọn là:A

Câu 28. Điều kiện xác định của phương trình 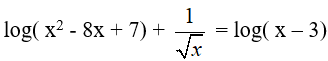 là:

A. 0 < x < 7

B. x > 7

C. 3 < x < 7

D. 0 < x < 3

Lời giải:

Điều kiện phương trình:

 

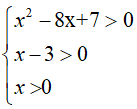
⇔ x > 7

Đáp án cần chọn là:B

Câu 29. Phương trình 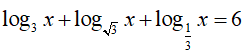 có nghiệm là:

A. x = 27

B. x = 9

C. x = 3

D. x = log₃6

Lời giải:

Điều kiện x > 0

⇔ log₃x + 2log₃x − log₃x = 6

2log₃x = 6 ⇔ log₃x = 3 ⇔ x = 27

Đáp án cần chọn là:A

Câu 30. Phương trình 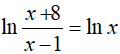 có nghiệm là:

A. x= − 2

B. x = 4 hoặc x = −2

C. x = 4

D. x = 1

Lời giải:

    

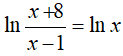
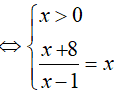
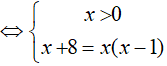
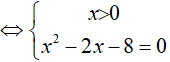
⇔ x = 4

Đáp án cần chọn là:C

Câu 31. Số nghiệm của phương trình log₄ (x + 12). log_x2 = 1 là:

A. 0.

B. 2.

C. 3.

D. 1.

Lời giải:

Điều kiện : 0 < x ≠ 1

     

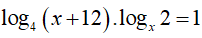
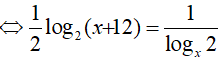
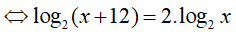
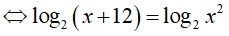
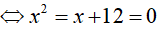
Vậy phương trình đã cho có 1 nghiệm là x=4.

Đáp án cần chọn là:D

Câu 32. Phương trình log_{2x − 3}(3² − 7x + 3) − 2 = 0 có nghiệm là:

A. x = 2; x= 3

B. x= 2 

C. x= 3

D. x= 1, x= 5

Lời giải:

Điều kiện: 

   

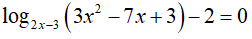
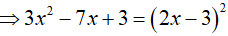
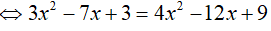
Kết hợp với điều kiện, ta có nghiệm phương trình là x= 3

Đáp án cần chọn là:D

Câu 33. Số nghiệm nguyên dương của phương trình 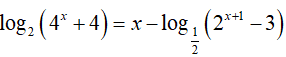 là:

A. 2.

B. 1.

C. 3.

D. 0.

Lời giải:

Điều kiện: 2^{x + 1} − 3 > 0 ⇔ x > log₂3 − 1

Ta có:

   

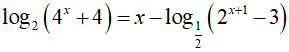
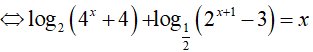
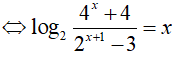
Đặt t = 2^x(t > 0)

Ta có

⇔ t² − 3t − 4 = 0 => t = 4

Do đó, 2^x = 4 ⇔ x = 2 (thỏa mãn điều kiện)

Vậy nghiệm của phương trình đã cho là x = 2.

Đáp án cần chọn là:B

Câu 34. Số nghiệm của phương trình log₄(log₂x) + log₂(log₄x) = 2 là:

A. 0.

B. 2.

C. 3.

D. 1.

Lời giải:

Phương trình đã cho tương đương:

      

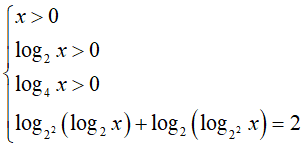
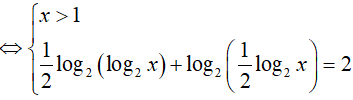
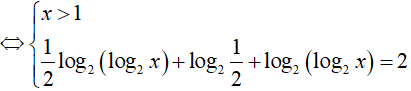
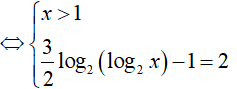
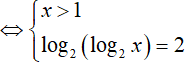
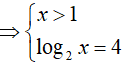
=> x = 16

Đáp án cần chọn là:D

Câu 35. Phương trình log₂²x − 4log₂x + 3 = 0 có tổng các nghiệm là:

A. 6

B. 8

C. 2

D. 10

Lời giải:

Điều kiện: x > 0

Đặt log₂ x= t. Khi đó, phương trình đã cho trở thành

   

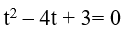
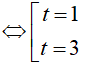
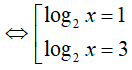
Kết hợp với điểu kiện, phương trình đã cho có 2 nghiệm là x= 2 và x= 8.

Tổng các nghiệm của phương trình là: S = 2 + 8 =10

Đáp án cần chọn là:D

Câu 36. Phương trình log₅²(2x − 1) − 8log₅√(2x − 1) + 3 = 0 có tổng các nghiệm là:

A. 4

B. 10

C. 26

D. 66

Lời giải:

Điều kiện 

 

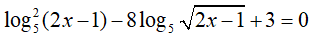
Đặt t= log₅ (2x − 1). Khi đó, phương trình (*) trở thành:

    

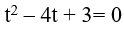
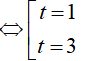
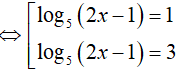
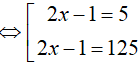
Do đó, tổng các nghiệm của phương trình đã cho là: 63 + 3= 66.

Đáp án cần chọn là:D

Câu 37. Số nghiệm của phương trình log₂x . log₃(2 − 1) = 2log₂x là:

A. 2.

B. 0.

C. 1.

D. 3.

Lời giải:

PT

     

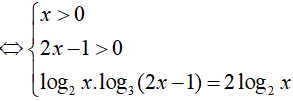
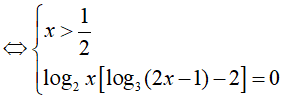
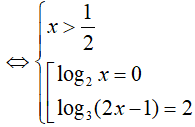
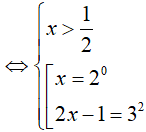
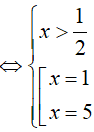
So điều kiện suy ra phương trình có nghiệm x= 3.

Đáp án cần chọn là:A

Câu 38. Tìm tất cả các giá trị thực của tham số m để phương trình log₃x − log₃(x − 2) = log_√3m có nghiệm?

A. m > 1.

B. m ≥ 1.

C. m < 1

D. m ≤ 1.

Lời giải:

Điều kiện: x > 2 và m > 0.

  

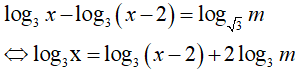
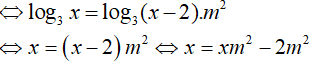
Phương trình có nghiệm x > 2 khi đó:

  

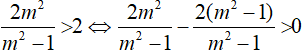
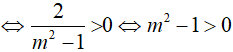
Kết hợp điều kiện m > 0 ta được m > 1 .

Đáp án cần chọn là:A

Câu 39. Tìm tất cả các giá trị thực của tham số m để phương trình 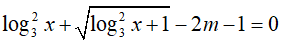có ít nhất một nghiệm thuộc đoạn [1; 3^√3] ?

A. m ∈ [0; 2].

B. m ∈ (0; 2).

C. m ∈ (0; 2].

D. m ∈ [0; 2).

Lời giải:

Với x ∈ [1; 3^√3] hay 1 ≤ x ≤ 3^√3

 

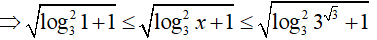
Đặt t = √(log₃²x + 1); t ∈ [1; 2]

Phương trình đã cho trở thành: t² − 1 + t − 2m − 1 = 0 hay t² + t − 2= 2m

Khi đó bài toán trở thành:Tìm m để phương trình t² + t − 2 = 2m có ít nhất một nghiệm thuộc đoạn [1; 2].

Xét hàm số f(t) = t² + t − 2, ∀t ∈ [1; 2], f'(t) = 2t + 1 > 0, ∀t ∈ [1; 2]

Suy ra hàm số đồng biến trên [1; 2].

Ta có bảng biến thiên của hàm số.

Khi đó phương trình có nghiệm khi 0 ≤ 2m ≤ 4 ⇔ 0 ≤ m ≤ 2

Vậy 0 ≤ m ≤ 2 là các giá trị cần tìm.

Đáp án cần chọn là:A

Câu 40. Tìm tất cả các giá trị của tham số m để phương trình log₂(5^x − 1).log₄(2.5^x − 2 ) = m có nghiệm x ≥ 1 ?

A. m ∈ [2; +∞).

B. m ∈ [3; +∞). 

C. m ∈ (−∞; 2].

D. m ∞ (−∞; 3].

Lời giải:

Ta có: log₂(5^x − 1).log₄(2.5^x − 2 )

Đặt t = log₂ (5^x − 1). Khi đó, phương trình đã cho trở thành:

Với x ≤ 1 => 5^x ≤ 5 => log₂(5^x − 1) ≤ log₂(5 − 1)hay t ≥ 2 .

Khi đó bài toán trở thành: Tìm m để phương trình t² + t = 2m có nghiệm

Xét hàm số f(t) = t² + t, ∀t ≥ 2, f'(t) = 2t + 1 > 0, ∀t ≥ 2

Suy ra hàm số đồng biến với t ≥ 2.

Khi đó phương trình có nghiệm khi 2m ≥ 6 ⇔ m ≥ 3

Vậy m ≥ 3 là các giá trị cần tìm.

Đáp án cần chọn là:B

Câu 41. Tìm tất cả các giá trị thực của tham số m để phương trình log₃²x − (m + 2)log₃x + 3m − 1 = 0 có hai nghiệm x1; x2 thỏa mãn x₁.x₂ = 27?

A. m = −2

B. m = −

C. m = 1

D. m = 27

Lời giải:

Đặt t = log₃x. Khi đó phương trình có dạng: t² − (m + 2).t + 3m − 1 = 0 (1).

Để phương trình có hai nghiệm phân biệt thì

Δ = (m + 2)² − 4(3m − 1) = m² − 8m + 8 > 0

Với điều kiện (*), phương trình (1) có 2 nghiệm t1 ; t2 và :

t₁ + t₂ = log₃x₁ + log₃x₂ = log₃ (x₁.x₂) = log₃27 = 3

Theo Vi-ét ta có: t₁ + t₂ = m + 2. Do đó, m+ 2 = 3 ⇔ m= 1 (thỏa mãn điều kiện)

Vậy m = 1 là giá trị cần tìm.

Đáp án cần chọn là:C

Câu 42. Tìm tất cả các giá trị thực của tham số m để phương trình 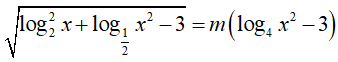có nghiệm thuộc [32; +∞)?

A. m ∈ (1; √3].

B. m ∈ [1; √3).

C. m ∈ [−1; √3). 

D. m ∈ (−√3; 1]

Lời giải:

Điều kiện: x > 0.Khi đó phương trình tương đương:

Đặt t = log₂x với x ≥ 32 => log₂x ≥ log₂32 = 5 hay t ≥ 5

Phương trình đã cho trở thành : √(t² − 2t − 3) = m(t − 3) (*).

Khi đó bài toán trở thành : Tìm m để phương trình (*) có nghiệm t ≥ 5 ”

Với t ≥ 5 thì (*)

   

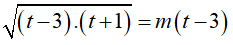
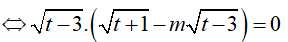
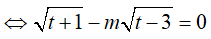
Ta có:

Với

hay

Suy ra 1 < m ≤ √3 Vậy phương trình có nghiệm với 1 < m ≤ √3

Đáp án cần chọn là:C

Câu 43: Giả sử x là nghiệm của phương trình

A. 0

B. ln3

C. –ln3

D. 1/ln3

Lời giải:

Để ý rằng

nên phương trình đã cho tương đương với

Đáp án cần chọn là:A

Câu 44: Tính tích tất cả các nghiệm của phương trình 3^{2x2 + 2x + 1} - 28.3^{x2 + x} + 9 = 0

A. -4

B. -2

C. 2

D. 4

Lời giải:

Ta có: 3^{2x2 + 2x + 1} -28.3^{x2 + x} + 9 = 0 ⇔ 3.3^{2(x2 + x)} - 28.3^{x2 + x} + 9 = 0

Đặt t = 3^x2 + x > 0 nhận được phương trình

Với t = 1/3 = 3^-1 được 3^{x2 + x} = 3^-1 ⇔ x² + x + 1 = 0(vô nghiệm)

Với t = 9 được phương trình 3^{x2 + x} = 9 = 3² ⇔ x² + x = 2

x² + x - 2 = 0 ⇔ x -2 hoặc x = 1

Tích của hai nghiệm này bằng -2.

Đáp án cần chọn là:B

Câu 45: Giải phương trình (x² - 2x)lnx = lnx³

A. x = 1, x = 3

B. x = -1, x = 3

C. x = ±1, x = 3

D. x = 3

Lời giải:

Điều kiện x > 0. Khi đó phương trình đã cho tương đương với

(x² -2x)lnx = 3lnx ⇔ (x² - 2x + 3)lnx = 0

Vậy phương trình có hai nghiệm là x = 1, x = 3 .

Chọn đáp án A.

Chú ý. Sai lầm thường gặp là quên điều kiện dẫn đến không loại được nghiệm x = -1 và chọn phương án nhiễu C.

Thậm chí, có thể học sinh biến đổi (x² - 2x)lnx = 3lnx ⇔ x² -2x = 3(giản ước cho lnx) dẫn đến mất nghiệm x = 1 và chọn phương án nhiễu D.

Đáp án cần chọn là:A

Câu 46:Giải phương trình logx = log(x + 3) - log(x - 1)

A. x = 1

B. x = 3

C. x = 4

D. x = -1, x = 3

Lời giải:

Điều kiện x > 1. Khi đó phương trình tương đương với

Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.

Đáp án cần chọn là:B

Câu 47: Giải phương trình log_√2(x + 1) = log₂(x² + 2) - 1

A. x = 1 

B. x = 0

C. x = 0, x = -4

D. x = 0, x = 1

Lời giải:

Điều kiện x > -1. Khi đó phương trình tương đương với

2log₂(x + 1) = log₂(x² + 2)

Đáp án cần chọn là:B

Câu 48: Cho biết log_b²x + log_x²b = 1, b > 0, b ≠ 1, x ≠ 1. Khi đó x bằng:

A. b

B. √b

C. 1/b

D. 1/b²

Lời giải:

Điều kiện: x > 0

Đáp án cần chọn là:A

Câu 49: Cho biết 2^x = 8^{y + 1} và 9^y = 3^{x - 9} . Tính giá trị của x + y

A. 21

B. 18

C. 24

D. 27

Lời giải:

Vậy x + y =27.

Đáp án cần chọn là:D

Câu 50: Giả sử x, y là hai số thực thỏa mãn đồng thời 3^{x2 - 2xy} = 1 và 2log₃x = log₃(y + 3). Tính x + y

A. 9/4

B. 3/2

C. 3

D. 9

Lời giải:

Điều kiện x > 0, y > -3.

Ta có: 3^{x2 - 2xy} = 1 = 3⁰ ⇔ x² - 2xy = 0

⇔ x(x - 2y) = 0 ⇔ x - 2y = 0 (x > 0) ⇔ x = 2y (1)

2log₃x = log₃( y + 3) ⇔ log₃x² = log₃(y + 3) ⇔ x² = y + 3 (2)

Thế (1) vào (2) ta được:

Đáp án cần chọn là:C