Toptailieu.vn xin giới thiệu 51 câu trắc nghiệm Phép vị tự (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 11 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán. Tài liệu gồm có các nội dung chính sau:

Mời các bạn đón xem:

51 câu trắc nghiệm Phép vị tự (có đáp án) chọn lọc

Câu 1: Trong mặt phẳng tọa độ Oxy cho đường (C) có phương trình.

   x² + y² - 4x + 6y - 3 = 0. Qua phép vị tự tâm H(1;3) tỉ số k = -2, đường tròn (C) biến thành đường tròn (C’) có phương trình.

A.  x² + y² + 2x - 30y + 60 = 0

B.   x² + y² - 2x - 30y + 62 = 0

C.   x² + y² + 2x - 30y + 62 = 0

D.  x² + y² - 2x - 30y + 60 = 0

Lời giải:

Đáp án: C

   (C)  (x - 2)² + (y + 3)² = 16 tâm I(2;-3), bán kính R = 4.    V_(H;-2)(I) = I'(x;y)  HI'→ = -2HI→

Câu 2: Cho hai đường thẳng d và d’ cắt nhau. Có bao nhiêu phép vị tự biến d thành d’?

   A. không có phép vị tự nào      B. có một phép vị tự duy nhất

   C. có hai phép vị tự                  D. có vô số phép vị tự

Lời giải:

Đáp án: A

Không có phép vị tự nào biến d thành d’ (Phép vị tự biến một đường thẳng thành đường thẳng song song hoặc trùng với nó).

Câu 3: Cho hai đường tròn (O;R) và (O’;R) (O không trùng với O’). Có bao nhiều phép vị tự biến (O) thành (O’)?

A. không có phép vị tự nào     

B. có một phép vị tự duy nhất

C. có hai phép vị tự                 

D. có vô số phép vị tự

Lời giải:

Đáp án: B

   Có một phép vị tự duy nhất, tâm vị tự là trung điểm OO’, tỉ số vị tự là k = -1.

Câu 4: Có bao nhiêu phép vị tự biến một đường tròn thành chính nó?

A. không có phép vị tự nào     

B. có một phép vị tự duy nhất

C. có hai phép vị tự                 

D. có vô số phép vị tự

Lời giải:

Đáp án: C

   (hình 1) Có hai phép vị tự: V_{(O; 1)}(O; OA) = (O; OA) và V_{(0; -1)}(O; OA) = (O; OB)

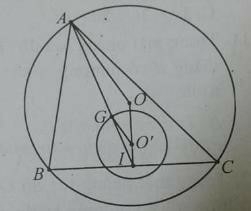
Câu 5: Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC , G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây?

A.  phép vị tự tâm A tỉ số k = 2/3

B.   phép vị tự tâm A tỉ số k = -2/3

C.   phép vị tựu tâm I tỉ số k = 1/3   

D. phép vị tự tâm I tỉ số k = -1/3

Lời giải:

Đáp án: C

    B, C cố định nên trung điểm I của BC cũng cố định. G là trọng tâm tam giác ABC nên ta có  = 1/3   có phép vị tự I tỉ số k = 1/3 biến A thành G. A chạy trên (O) nên G chạy trên (O’) ảnh của O qua phép vị tự trên.

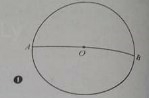
Câu 6: Cho tam giác ABC nội tiếp đường tròn (O;R). điểm A cố định, dây BC có độ dài bằng R; G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?

Lời giải:

Đáp án: C

(hình 2) Ta có tam giác OBC đều, đường cao OI = (R√3)/2

 I chạy trên đường tròn tâm O bán kính (R√3)/2.

A cố định, G là trọng tâm ta giác ABC nên  = 2/3     có phép vị tự tâm A tỉ số k = 2/3 biến đường tròn (O;(R√3)/2) thành đường

tròn (O';R’) với

Lời giải:

Đáp án: C

   Lấy điểm A, A’ bất kì lần lượt trên d và d’.

   Trên đường thẳng AA’ lấy điểm I bất kì, đặt IA'/IA = k.

   Khi đó, phép vị tự tâm I tỉ số k biến A thành A’, biến đường thẳng d thành đường thẳng d’.

Vì A và A’ là 2 điểm bất kì trên d và d’ nên có vô số phép vị tự biến d thành d’

Đáp án C

Câu 8: Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.

   Phép vị tự tâm G tỉ số -1/2 biến:

A. Điểm A thành điểm G     

B. Điểm A thành điểm D

C. Điểm D thành điểm A     

D. Điểm G thành điểm A

   b) Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành

A. Tam giác GBC     

B. Tam giác DEF

C. Tam giác AEF     

D. Tam giác AFE

   c) Phép vị tự tâm G tỉ số -1/2 biến  thành

   A.       B. 

   C.       D. 

Lời giải:

Đáp án: B

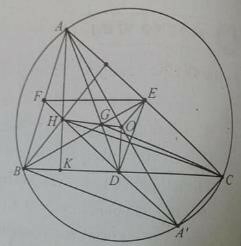
a)     = -1/2   phép vị tự tâm G tỉ số -1/2 biến A thành D. Đáp án B.

b)    Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F  

biến tam giác ABC thành tam giác DEF. Đáp án B

c)     Gọi A’ là điểm đối xứng với A qua tâm O. Chứng mình BHCA’ là hình bình hành, suy ra H; A’; D thẳng hàng và DO là đường trung bình của tam giác AHA’   = -1/2       phép vị tự tâm G tỉ số -1/2 biến  thành .

Câu 9: Trong mặt phẳng tọa độ Oxy phép vị tự H(1;2) tỉ số k = -3 điểm M(4;7) biến thành điểm M’ có tọa độ

   A. M'(-13;-8)      B. M'(8;13)    C. M'(-8;-13)      D. M'(-8;13)

Lời giải:

Đáp án: C

Câu 10: Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình : 3x + y

+ 6 = 0. Qua phép vị tự tâm O(0;0) tỉ số k = 2, đường thẳng d biến thành đường thẳng d’ có phương trình.

A.  -3x + y - 6 = 0

B.   -3x + y + 12 = 0

C.   3x - y + 12 = 0   

D. 3x + y + 18 = 0

Lời giải:

Đáp án: D

   Lấy M(-2;0) thuộc d. Phép vị tự tâm O (0;0) tỉ số k = 2 biến d thành d’//d và biến M thành M’ thì  = 2  M'(-4;0). Phương trình d’: 3(x + 4) + y + 6 = 0  3x + y + 18 = 0. Đáp án D.

Câu 11: Cho hình thang ABCD có AD // BC và AD = 2 BC. Gọi O là giao điểm hai đường chéo hình thang. Phép vị tự tâm A biến C thành O có tỉ số vị tự là:   

A. k = 3/2   

B.   k = 2/3   

C.   k = 2   

D.  k = 3

Lời giải:

Đáp án: B

   Vì BC // AD nên áp dụng hệ quả định lí ta – let ta có:

Câu 12: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ có tọa độ

A.  M'(-12;-9)   

B.   M'(12;9)

C.   M'(-9;12)    

D.  M'(12;-9)

Lời giải:

Đáp án: D

    = -3

   A. M'(1;-5)   

   B.M'(8;13)

   C. M'(6;-23)   

   D.M'(6;-27)

Lời giải:

Đáp án: C

Câu 15: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -5, biến đường thẳng d có phương trình : 2x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:

A.  2x + 3y - 16 = 0

B.   3x + 2y - 4 = 0

C.   3x + 2y - 20 = 0    D. 2x + 3y + 20 = 0

Lời giải:

Đáp án: D

   Phép vị tự tâm O(0; 0) tỉ số k = -5, biến M(x; y) thuộc d thành M’(x’, y’) thuộc d’   = -5

Câu 16: Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;4) tỉ số k = -2, biến đường thẳng d có phương trình : 7x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:

A.  7x + 3y - 49 = 0

B.   3x + 7y - 47 = 0

C.   7x + 3y + 49 = 0

D.  3x + 7y - 49 = 0

Lời giải:

Đáp án: A

   Phép vị tự tâm I (1; 4) tỉ số k = -2, biến M(x; y) thuộc d thành M’(x’;y’) thuộc d;

   IM'→ = -2IM→

Lời giải:

Đáp án: B

   Phép vị tự tâm O(0; 0) tỉ số k = -2 biến tâm O của (C) thành O, biến bán kính R = 3 thành R’ = 6  phương trình (C’) là x² + y² = 36

Câu 18: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = 2 biến đường tròn (C) có phương trình: x² + y² + 4x + 6y = 12 thành đường tròn (C’) có phương trình:

A.  (x - 4)² + (y - 6)² = 100

B.   (x + 2)² + (y + 3)² = 100

C.   (x + 4)² + (y + 6)² = 100

D.  (x - 2)² + (y - 3)² = 100

Lời giải:

Đáp án: C

   (C)  (x + 2 )² + (y + 3)² = 25. Phép vị tự tâm O(0; 0) tỉ số k = 2 biến tâm I(-2; 3) của (C) thành I’(-4; -6), biến bán kính R = 5 thành R’ = 10  phương trình (C’) là: (x + 4)² + (y + 6)² = 100

Câu 19: Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;0) tỉ số k = 2, biến đường tròn (C) có phương trình : x² + 4x + y² + 6y = 12 thành đường tròn (C’) có phương trình

A.  (x - 5)² + (y - 6)² = 100

B.   (x + 5)² + (y + 6)² = 100

C.   (x + 4)² + (y + 6)² = 100

D.  (x - 2)² + (y - 3)² = 100

Lời giải:

Đáp án: B

   (C)  (x + 2 )² + (y + 3 )² = 25. Phép vị tự tâm H(1; 0) tỉ số k = 2, biến tâm I(-2;

-3) của (C) thành I’(x;y)

biến bán kính R = 4√2 thành R' = 2√2  phương trình (C’) là:

Đáp án: C

   Lấy điểm A, A’ bất kì lần lượt trên d và d’.

   Trên đường thẳng AA’ lấy điểm I bất kì, đặt IA'/IA = k.

   Khi đó, phép vị tự tâm I tỉ số k biến A thành A’, biến đường thẳng d thành đường thẳng d’.

   Vì A và A’ là 2 điểm bất kì trên d và d’ nên có vô số phép vị tự biến d thành d’

   Đáp án C

Câu 22: Cho tam giác ABC có trọng tâm G, trực tâm H, tâm đường tròn ngoại tiếp O. gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB.

   Phép vị tự tâm G tỉ số -1/2 biến:

 A. Điểm A thành điểm G     

B. Điểm A thành điểm D

C. Điểm D thành điểm A     

D. Điểm G thành điểm A

   b) Phép vị tự tâm G tỉ số -1/2 biến tam giác ABC thành

A. Tam giác GBC     

B. Tam giác DEF

C. Tam giác AEF     

D. Tam giác AFE

   c) Phép vị tự tâm G tỉ số -1/2 biến AH→ thành

A. OD→     

B. DO→

C. HK→     

D. KH→

Lời giải:

Đáp án: B

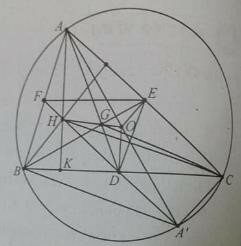
a)   GD→ = -1/2 GA→  phép vị tự tâm G tỉ số -1/2 biến A thành D. Đáp án B.

b)  Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F  

biến tam giác ABC thành tam giác DEF. Đáp án B

c)   Gọi A’ là điểm đối xứng với A qua tâm O. Chứng mình BHCA’ là hình bình hành, suy ra H; A’; D thẳng hàng và DO là đường trung bình của tam giác AHA’  DO→ = -1/2AH→       phép vị tự tâm G tỉ số -1/2 biến AH→ thành DO→.

Câu 23: Trong mặt phẳng tọa độ Oxy phép vị tự H(1;2) tỉ số k = -3 điểm M(4;7) biến thành điểm M’ có tọa độ

A.  M'(-13;-8)     

B. M'(8;13)   

C. M'(-8;-13)     

D. M'(-8;13)

Lời giải:

Đáp án: C

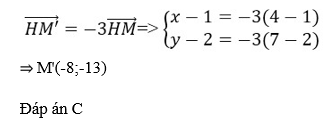
Đáp án C

Câu 24: Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình : 3x + y + 6 = 0. Qua phép vị tự tâm O(0;0) tỉ số k = 2, đường thẳng d biến thành đường thẳng d’ có phương trình.   

A. -3x + y - 6 = 0

A.  -3x + y + 12 = 0

B.  3x - y + 12 = 0   

D. 3x + y + 18 = 0

Lời giải:

Đáp án: D

   Lấy M(-2;0) thuộc d. Phép vị tự tâm O (0;0) tỉ số k = 2 biến d thành d’//d và biến M thành M’ thì OM'→ = 2OM→  M'(-4;0). Phương trình d’: 3(x + 4) + y + 6 = 0  3x + y + 18 = 0. Đáp án D.

Câu 25: Trong mặt phẳng tọa độ Oxy cho đường (C) có phương trình.

   x² + y² - 4x + 6y - 3 = 0. Qua phép vị tự tâm H(1;3) tỉ số k = -2, đường tròn (C) biến thành đường tròn (C’) có phương trình.

A.  x² + y² + 2x - 30y + 60 = 0

B.   x² + y² - 2x - 30y + 62 = 0

C.   x² + y² + 2x - 30y + 62 = 0

D.  x² + y² - 2x - 30y + 60 = 0

Lời giải:

Đáp án: C

   (C)  (x - 2)² + (y + 3)² = 16 tâm I(2;-3), bán kính R = 4.

   V_(H;-2)(I) = I'(x;y)  HI'→ = -2HI→

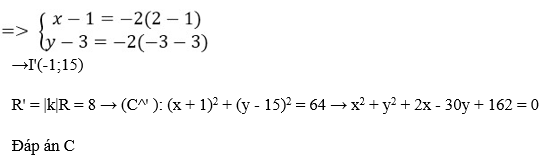
Câu 26: Cho hai đường thẳng d và d’ cắt nhau. Có bao nhiêu phép vị tự biến d thành d’?

A. không có phép vị tự nào     

B. có một phép vị tự duy nhất

C. có hai phép vị tự     

D. có vô số phép vị tự

Lời giải:

Đáp án: A

   Không có phép vị tự nào biến d thành d’ (Phép vị tự biến một đường thẳng thành đường thẳng song song hoặc trùng với nó).

Câu 27: Cho hai đường tròn (O;R) và (O’;R) (O không trùng với O’). Có bao nhiều phép vị tự biến (O) thành (O’)?

A. không có phép vị tự nào     

B. có một phép vị tự duy nhất

C. có hai phép vị tự     

D. có vô số phép vị tự

Lời giải:

Đáp án: B

   Có một phép vị tự duy nhất, tâm vị tự là trung điểm OO’, tỉ số vị tự là k = -1.

Câu 28: Có bao nhiêu phép vị tự biến một đường tròn thành chính nó?

A. không có phép vị tự nào     

B. có một phép vị tự duy nhất

C. có hai phép vị tự     

D. có vô số phép vị tự

Lời giải:

Đáp án: C

   (hình 1) Có hai phép vị tự: V_{(O; 1)}(O; OA) = (O; OA) và V_{(0; -1)}(O; OA) = (O; OB)

Câu 29: Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC , G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây?

A.  phép vị tự tâm A tỉ số k = 2/3

B.   phép vị tự tâm A tỉ số k = -2/3

C.   phép vị tựu tâm I tỉ số k = 1/3   

D. phép vị tự tâm I tỉ số k = -1/3

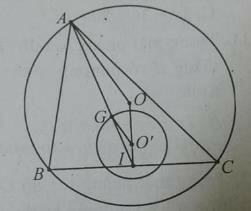
Lời giải:

Đáp án: C

    B, C cố định nên trung điểm I của BC cũng cố định. G là trọng tâm tam giác ABC nên ta có IG→ = 1/3 IA→  có phép vị tự I tỉ số k = 1/3 biến A thành G. A chạy trên (O) nên G chạy trên (O’) ảnh của O qua phép vị tự trên.

Câu 30: Cho tam giác ABC nội tiếp đường tròn (O;R). điểm A cố định, dây BC có độ dài bằng R; G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?

Lời giải:

Đáp án: C

   (hình 2) Ta có tam giác OBC đều, đường cao OI = (R√3)/2     I chạy trên đường tròn tâm O bán kính (R√3)/2.

   A cố định, G là trọng tâm ta giác ABC nên AG→ = 2/3 AI→    có phép vị tự tâm A tỉ số k = 2/3 biến đường tròn (O;(R√3)/2) thành đường

tròn (O';R’) với 

   Chọn đáp án C

Câu 31: Cho hình thang ABCD có AD // BC và AD = 2 BC. Gọi O là giao điểm hai đường chéo hình thang. Phép vị tự tâm A biến C thành O có tỉ số vị tự là:    A. k = 3/2   

B.   k = 2/3   

C.   k = 2   

D.  k = 3

Lời giải:

Đáp án: B

   Vì BC // AD nên áp dụng hệ quả định lí ta – let ta có:

Câu 32: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -3, biến điểm M(-4;3) thành điểm M’ có tọa độ

A.  M'(-12;-9)   

B.   M'(12;9)

C.   M'(-9;12)   

D.  M'(12;-9)

Lời giải:

Đáp án: D

   OM'→ = -3OM→

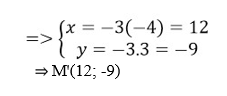
Câu 33: Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;2) tỉ số k = 5, biến điểm M(2;-3) thanh điểm M’ có tọa độ:

   A. M'(1;-5)   

   B.M'(8;13)

   C. M'(6;-23)   

   D.M'(6;-27)

Lời giải:

Đáp án: C

   IM'→ = 5IM→

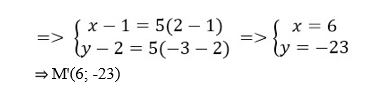
Câu 34: Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(0;2) tỉ số k = -1/2 , biến điểm M(12;-3) thành điểm M’ có tọa độ:

A.  M'(12;-1/2)   

B.   M'(-6;9/2)

C.   M'(6;-2)   

D.  M'(-6;12)

Lời giải:

Đáp án: B

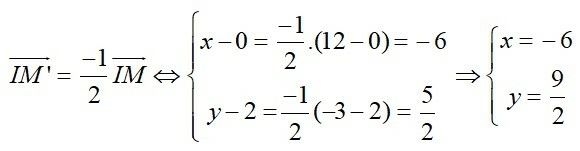
Câu 35: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -5, biến đường thẳng d có phương trình : 2x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:

A.  2x + 3y - 16 = 0

B.   3x + 2y - 4 = 0

C.   3x + 2y - 20 = 0    D. 2x + 3y + 20 = 0

Lời giải:

Đáp án: D

   Phép vị tự tâm O(0; 0) tỉ số k = -5, biến M(x; y) thuộc d thành M’(x’, y’) thuộc

d’  OM'→ = -5OM→

Câu 36: Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;4) tỉ số k = -2, biến đường thẳng d có phương trình : 7x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:

A.  7x + 3y - 49 = 0

B.   3x + 7y - 47 = 0

C.   7x + 3y + 49 = 0

D.  3x + 7y - 49 = 0

Lời giải:

Đáp án: A

   Phép vị tự tâm I (1; 4) tỉ số k = -2, biến M(x; y) thuộc d thành M’(x’;y’) thuộc d;

   IM'→ = -2IM→

Câu 37: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -2, biến đường tròn (C) có phương trình: x² + y² = 9 thành đường tròn (C’) có phương trình:

A.  x² + y² = 18

B.   x² + y² = 36

C.   x² + y² = 9

D.  x² + y² = 6

Đáp án: B

   Phép vị tự tâm O(0; 0) tỉ số k = -2 biến tâm O của (C) thành O, biến bán kính R = 3 thành R’ = 6  phương trình (C’) là x² + y² = 36

Câu 38: Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = 2 biến đường tròn (C) có phương trình: x² + y² + 4x + 6y = 12 thành đường tròn (C’) có phương trình:

A.  (x - 4)² + (y - 6)² = 100

B.   (x + 2)² + (y + 3)² = 100

C.   (x + 4)² + (y + 6)² = 100

D.  (x - 2)² + (y - 3)² = 100

Lời giải:

Đáp án: C

   (C)  (x + 2 )² + (y + 3)² = 25. Phép vị tự tâm O(0; 0) tỉ số k = 2 biến tâm I(-2; 3) của (C) thành I’(-4; -6), biến bán kính R = 5 thành R’ = 10  phương trình (C’) là: (x + 4)² + (y + 6)² = 100

Câu 39: Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;0) tỉ số k = 2, biến đường tròn (C) có phương trình : x² + 4x + y² + 6y = 12 thành đường tròn (C’) có phương trình

   A. (x - 5)² + (y - 6)² = 100 B. (x + 5)² + (y + 6)² = 100

C.   (x + 4)² + (y + 6)² = 100

D.  (x - 2)² + (y - 3)² = 100

Lời giải:

Đáp án: B

   (C)  (x + 2 )² + (y + 3 )² = 25. Phép vị tự tâm H(1; 0) tỉ số k = 2, biến tâm I(-2; -3) của (C) thành I’(x;y)

   HI'→ = 2HI→

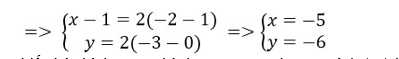
biến bán kính R = 5 thành R’ = 10  Phương trình (C’) là: (x + 5)² + (y + 6)² = 100

Câu 40: Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k = 1/2, biến đường tròn (C) có phương trình : (x - 2)² + (y - 3)² = 32 thành đường tròn (C’) có phương trình:

A.  (x - 3/2)² + y² = 16

B.   (x - 3/2)² + (y - 2)² = 8

C.   (x - 3)² + (y - 2)² = 32

D.  (x - 3/2)² + y² = 8

Lời giải:

Đáp án: D

    Phép vị tự tâm H (1; -3) tỉ số k = 1/2, biến tâm I(2; 3) của (C) thành I’(x; y)

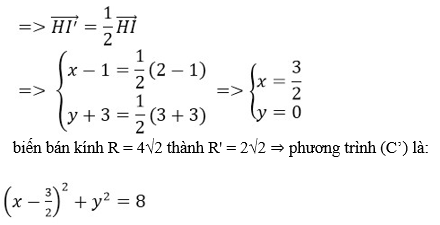
Câu 41. Trong mặt phẳng Oxy, cho đường thẳng d có phương trình 5x + 2y-7 = 0.

Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép vị tự tâm O tỉ số k = -2.

A.  5x + 2y + 14 = 0.

B.   5x + 2y + 7 = 0.

C.  5x - 2y + 14 = 0.

D.  5x + 2y - 14 = 0.

Lời giải:

Đáp án: A

Giải thích:

Lấy M(x;y) ∈ d ⇒ 5x + 2y - 7 = 0 (*).

Gọi M'(x';y') = V_(O,-2)(M).

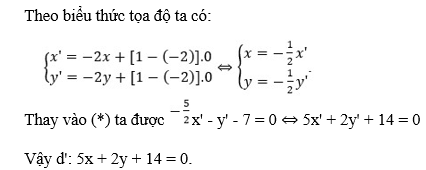
Câu 42. Tìm ảnh của các đt d sau qua phép vị tự tâm O, tỉ số k, biết: d: 4x – 3y + 1 = 0, k = -3

A.  4x – 2y – 3 = 0

B.   4x – 2y + 1 = 0

C.  12x + 9y – 3 = 0

D.  4x – 2y + 3 = 0

Lời giải:

Đáp án: A

Giải thích:

 Gọi V_(O,-3)(d) = d' ⇒ d’ // d nên PT đt d’ có dạng: 4x – 3y + C = 0

Chọn A(2; 3) ∈ d V_(O,-3)(A) = A' (-6; -9) ∈ d’. Khi đó: -24 + 27 + C = 0 ⇔ C = -3

Vậy: PT đt d’ là: 4x – 2y – 3 = 0

Câu 43. Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d) có phương trình 2x + 3y - 1 = 0 và điểm I(-1;3), phép vị tự tâm I tỉ số k = -3 biến đường thẳng (d) thành đường thẳng (d'). Viết phương trình đường thẳng (d')

A.  2x + 3y + 25 = 0

B.   2x + 3y – 25 = 0

C.  2x – 3y – 25 = 0

D.  6x – 9y – 3 = 0

Lời giải:

Đáp án: A

Giải thích:

Đường thẳng (d') có dạng: 2x + 3y + m = 0.

Lấy A(-1;1) ∈ (d), gọi A'(x;y) là ảnh của A qua

Đáp án: A

Giải thích:

Phép vị tự tâm I (1; 4) tỉ số k = -2, biến M(x; y) thuộc d thành M’(x’;y’) thuộc d;

⇒ vecto IM' = vecto -2IM

Câu 45. Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -2, biến đường tròn (C) có phương trình: x² + y² = 9 thành đường tròn (C’) có phương trình:

A.  x² + y² = 18

B.   x² + y² = 36

C.  x² + y² = 9

D.  x² + y² = 6

Lời giải:

Đáp án: B

Giải thích:

Phép vị tự tâm O(0; 0) tỉ số k = -2 biến tâm O của (C) thành O, biến bán kính R = 3 thành R’ = 6  phương trình (C’) là x² + y² = 36

Câu 46. Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = 2 biến đường tròn (C) có phương trình: x² + y² + 4x + 6y = 12 thành đường tròn (C’) có phương trình:

A.  (x - 4)² + (y - 6)² = 100

B.   (x + 2)² + (y + 3)² = 100

C.  (x + 4)² + (y + 6)² = 100

D.  (x - 2)² + (y - 3)² = 100

Lời giải:

Đáp án: C

Giải thích: (C)  (x + 2 )² + (y + 3)² = 25. Phép vị tự tâm O(0; 0) tỉ số k = 2 biến tâm I(-2; -3) của (C) thành I’(-4; -6), biến bán kính R = 5 thành R’ = 10  phương trình (C’) là: (x + 4)² + (y + 6)² = 100

Câu 47.Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k = 1/2, biến đường tròn (C) có phương trình : (x - 2)² + (y - 3)² = 32 thành đường tròn (C’) có phương trình:

A.  (x - 3/2)² + y² = 16

B.   (x - 3/2)² + (y - 2)² = 8

C.  (x - 3)² + (y - 2)² = 32

D.  (x - 3/2)² + y² = 8

Lời giải:

Đáp án: D

Giải thích:

Đáp án: B

Giải thích:

Đường tròn (C) có bán kính là R = 4.

Đường tròn (C') có bán kính là R' = 2.

Do (C) là ảnh của (C') qua phép vị tự tỉ số k ⇒ R = |k|R' ⇔ 4 = 2|k| ⇔ k = ±2.

Câu 49. Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;2) tỉ số k = 5, biến điểm M(2;-3) thanh điểm M’ có tọa độ:

A.  M'(1;-5)   

B.   M'(8;13)

C.  M'(6;-23)   

D.  M'(6;-27)

Lời giải:

Đáp án: C

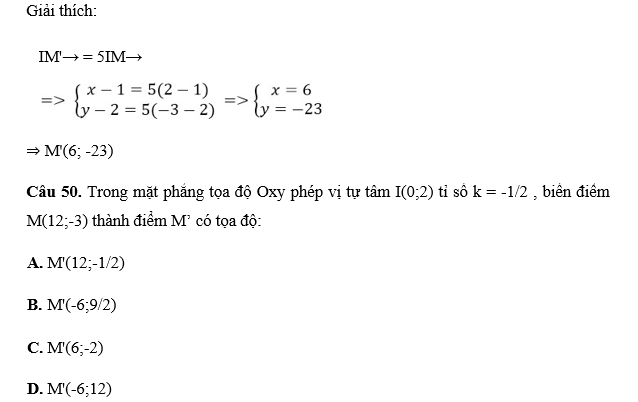
Đáp án: B

Giải thích:

Phép vị tự có tâm là trung điểm OO'OO', tỉ số vị tự bằng -1 .