Toptailieu.vn xin giới thiệu 25 câu trắc nghiệm Tập hợp. Các phép toán trên tập hợp (Cánh diều) có đáp án - Toán 10 chọn lọc, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
25 câu trắc nghiệm Tập hợp. Các phép toán trên tập hợp (Cánh diều) có đáp án - Toán 10
Câu 1. Kí hiệu A ∩ B nghĩa là:
A. Hợp của hai tập hợp A và B;
B. Giao của hai tập hợp A và B;
C. Hiệu của tập hợp A và tập hợp B;
D. Phần bù của tập hợp A trong tập hợp B.
Đáp án: B
Giải thích:
Hợp của hai tập hợp A và B được kí hiệu là A ∪ B.
Giao của hai tập hợp A và B được kí hiệu là A ∩ B.
Hiệu của A và B được kí hiệu là A \ B.
Cho A ⊂ B, khi đó phần bù của A trong B được kí hiệu là CBA.
Vậy ta chọn đáp án B.
Câu 2. Trong các khẳng định sau, khẳng định nào sai?
A. x ∈ A \ B Þ x ∈ A;
B. x ∈ CEA Þ x ∉ A;
C. x ∈ A \ B Þ x ∉ B;
D. x ∈ A ∩ B Þ x ∈ A hoặc x ∈ B.
Đáp án: D
Giải thích:
⦁ Ta có A \ B = {x | x ∈ A và x ∉ B}.
Do đó phương án A, C đúng.
⦁ Kí hiệu CEA dùng để chỉ phần bù của A trong E, với A ⊂ E.
Do đó nếu x ∈ CEA thì x ∉ A.
Vì vậy phương án B đúng.
⦁ Ta có A ∩ B = {x | x ∈ A và x ∈ B}.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 3. Cho A = {1; 2; 4; 5} và B = {–2; –1; 0; 1; 2}. Khi đó A ∪ B là tập hợp:
A. {1; 2};
B. {–2; –1; 0; 1; 2; 4; 5};
C. {4; 5};
D. {–2; –1; 0}.
Đáp án: B
Giải thích:
Với A = {1; 2; 4; 5} và B = {–2; –1; 0; 1; 2}.
Khi đó A ∪ B là hợp của tập hợp A và tập hợp B, gồm tất cả các phần tử thuộc A hoặc B.
Þ A ∪ B = {–2; –1; 0; 1; 2; 4; 5}.
Ta chọn phương án B.
Câu 4. Cho tập E = {2; 4; 6; 9}, F = {1; 2; 3; 4}. Tập nào sau đây bằng tập E \ F?
A. {1; 2; 3; 5};
B. {1; 3; 6; 9};
C. {6; 9};
D. {1}.
Đáp án: C
Giải thích:
Tập E \ F bao gồm các phần tử thuộc tập E nhưng không thuộc tập F.
Các phần tử thuộc E nhưng không thuộc F là: 6; 9.
Do đó E \ F = {6; 9}.
Vậy ta chọn phương án C.
Câu 5. Cho hai tập hợp U = {1; 2; 3; 4}, V = {1; 2}. Tập CUV là tập hợp nào sau đây?
A. {1; 2};
B. {1; 2; 3; 4};
C. {3; 4};
D. ∅.
Đáp án: C
Giải thích:
Với U = {1; 2; 3; 4}, V = {1; 2} ta thấy V ⊂ U.
Tập CUV (= U \ V) bao gồm các phần tử thuộc U nhưng không thuộc V.
Các phần tử thuộc U nhưng không thuộc V là: 3; 4.
Do đó CUV = {3; 4}.
Vậy ta chọn phương án C.
Câu 6. Cho A ≠ ∅. Trong các mệnh đề sau, mệnh đề nào sai?
A. A ∪ ∅ = ∅;
B. ∅ ∪ A = A;
C. ∅ ∪ ∅ = ∅;
D. A ∪ A = A.
Đáp án: A
Giải thích:
Phương án B, C, D đúng.
Phương án A sai. Sửa lại: A ∪ ∅ = A.
Vậy ta chọn phương án A.
Câu 7. Cho hai tập hợp A và B khác rỗng thỏa mãn A ⊂ B. Trong các mệnh đề sau, mệnh đề nào sai?
A. A ∩ B = A;
B. A \ B = ∅;
C. B \ A = B;
D. A ∪ B = B.
Đáp án: C
Giải thích:
Ta có sơ đồ Ven biểu diễn A ⊂ B như sau:
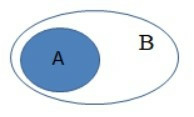
Quan sát sơ đồ Ven, ta thấy:
⦁ A ∩ B = A. Suy ra phương án A đúng.
⦁ A \ B = ∅. Suy ra phương án B đúng.
⦁ B \ A = CBA (phần không tô màu trên biểu đồ Ven). Suy ra phương án C sai.
⦁ A ∪ B = B. Suy ra phương án D đúng.
Vậy ta chọn phương án C.
Câu 8. Khẳng định nào sau đây sai?
A. ℤ ∪ ℚ = ℚ;
B. ℕ ∪ ℕ* = ℕ*;
C. ℚ ∩ ℝ = ℚ;
D. ℕ* ∩ ℝ = ℕ*.
Đáp án: B
Giải thích:
Ta có quan hệ bao hàm: ℕ* Ì ℕ Ì ℤ Ì ℚ Ì ℝ.
Khi đó:
• ℤ ∪ ℚ = ℚ. Do đó A đúng;
• ℕ ∪ ℕ* = ℕ. Do đó B sai;
• ℚ ∩ ℝ = ℚ. Do đó C đúng;
• ℕ* ∩ ℝ = ℕ*. Do đó D đúng.
Vậy ta chọn phương án B.
Câu 9. Cho tập hợp A = (–∞;–2] và tập B = (–1; +∞). Khi đó A ∪ B là:
A. (–2; +∞);
B. (–2; –1];
C. ℝ;
D. ∅.
Đáp án: C
Giải thích:
Để xác định tập hợp A ∪ B, ta vẽ sơ đồ sau đây:
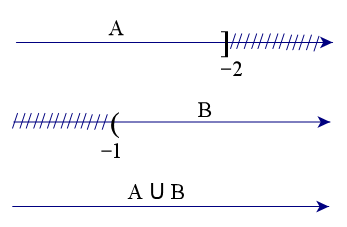
Từ sơ đồ, ta thấy A ∪ B = ℝ.
Vậy ta chọn phương án C.
Câu 10. Cho tập hợp C = [–5; 3), D = (1; +∞). Khi đó C ∩ D là tập nào sau đây?
A. (1; 3);
B. (1; 3];
C. [–5; +∞);
D. [–5; 1].
Đáp án: A
Giải thích:
Để xác định tập hợp C ∩ D, ta vẽ sơ đồ sau đây:
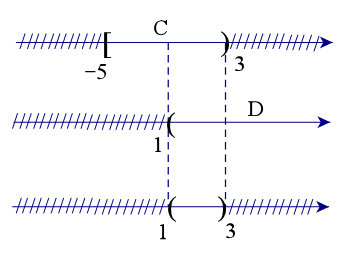
Từ sơ đồ, ta thấy C ∩ D = (1; 3).
Vậy ta chọn phương án A.
Câu 11. Cho hai tập hợp G = (1; 5]; H = (2; 7]. Tập hợp G \ H là:
A. (1; 2];
B. (2; 5);
C. (–1; 7];
D. (–1; 2).
Đáp án: A
Giải thích:
Để xác định tập hợp G \ H, ta vẽ sơ đồ sau đây:
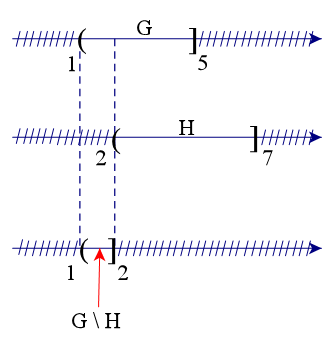
Từ sơ đồ, ta thấy G \ H = (1; 2] (vì tập H không lấy số 2 nên phần bù sẽ lấy số 2).
Vậy ta chọn phương án A.
Câu 12. Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ Ven như hình vẽ.
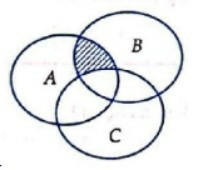
Phần gạch sọc trong hình vẽ là tập hợp nào sau đây?
A. (A ∪ B) \ C;
B. (A ∩ B) \ C;
C. (A \ C) ∪ (A \ B);
D. (A ∩ B) ∪ C.
Đáp án: B
Giải thích:
Quan sát hình vẽ, ta thấy mỗi phần tử x thuộc phần gạch sọc đều thỏa mãn cả 3 yêu cầu sau:
⦁ x ∈ A;
⦁ x ∈ B;
⦁ x ∉ C.
Vì x ∈ A và x ∈ B nên ta có x ∈ (A ∩ B).
Vì x ∈ (A ∩ B) và x ∉ C nên ta có x ∈ (A ∩ B) \ C.
Vậy ta chọn phương án B.
Câu 13. Cho hai tập hợp M = {1; 2; 4; 7; 9} và N = {–1; 0; 7; 10}. Tập hợp M \ N có bao nhiêu phần tử?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: D
Giải thích:
Ta có M \ N là tập hợp gồm những phần tử thuộc M nhưng không thuộc N.
Do đó ta có các phần tử: 1; 2; 4; 9.
Vậy M \ N = {1; 2; 4; 9} có 4 phần tử.
Ta chọn phương án D.
Câu 14. Cho hai tập hợp A = {1; 2; a; b} và B = {1; x; y} với x, y khác a, b, 2, 1. Kết luận nào sau đây là đúng?
A. A ∩ B = B;
B. A ∩ B = ∅;
C. A ∩ B = A;
D. A ∩ B = {1}.
Đáp án: D
Giải thích:
Vì x, y khác a, b, 2, 1 nên A và B có một phần tử chung là 1.
Do đó A ∩ B = {1}.
Ta chọn phương án D.
Câu 15. Cho A: “Tập hợp các học sinh khối 10 học giỏi”, B: “Tập hợp các học sinh nữ khối 10 học giỏi”, C: “Tập hợp các học sinh nam khối 10 học giỏi”. Vậy tập hợp C là:
A. A ⊂ B;
B. B \ A;
C. A ∩ B;
D. A \ B.
Đáp án: D
Giải thích:
Vì tập hợp B là tập hợp các học sinh nữ khối 10 học giỏi nên tập hợp C gồm những phần tử thuộc tập hợp A mà không thuộc tập hợp B.
Do đó C = A \ B.
Ta chọn phương án D.
Câu 16. Cho tập hợp 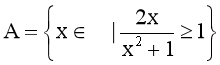 ; B là tập hợp tất cả các giá trị nguyên của b sao cho phương trình x2 – 2bx + 4 = 0 vô nghiệm. Số phần tử chung của hai tập hợp trên là:
; B là tập hợp tất cả các giá trị nguyên của b sao cho phương trình x2 – 2bx + 4 = 0 vô nghiệm. Số phần tử chung của hai tập hợp trên là:
A. 1;
B. 2;
C. 3;
D. 0.
Đáp án: A
Giải thích:
⦁ Xét tập hợp A:
Ta có 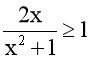 .
.
Û 2x ≥ x2 + 1 (do x2 + 1 > 0)
Û x2 – 2x + 1 ≤ 0.
Û (x – 1)2 ≤ 0.
Mà (x – 1)2 ≥ 0 với mọi x.
Nên (x – 1)2 ≤ 0 Û x – 1 = 0
Û x = 1 ∈ ℝ.
Vì vậy A = {1}.
⦁ Xét tập hợp B:
Xét phương trình x2 – 2bx + 4 = 0 (*)
∆’ = b2 – 4.
Phương trình (*) vô nghiệm Û ∆’ < 0.
Û b2 – 4 < 0.
Û –2 < b < 2.
Vì b là số nguyên nên ta nhận b = –1; b = 0; b = 1.
Suy ra tập B = {–1; 0; 1}.
Tập A ∩ B = {1}.
Vậy số phần tử chung của tập A và tập B là 1 phần tử.
Do đó ta chọn phương án A.
Câu 17. Cho ba tập hợp A = [–2; 2], B = [1; 5], C = [0; 1]. Khi đó tập (A \ B) ∩ C là:
A. {0; 1};
B. [0; 1);
C. (–2; 1);
D. [–2; 5].
Đáp án: B
Giải thích:
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
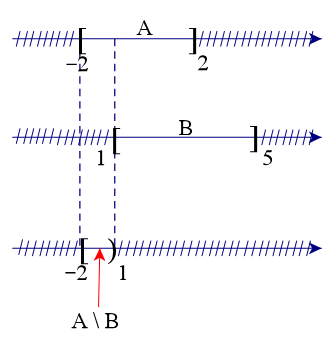
Từ sơ đồ, ta thấy A \ B = [–2; 1) (vì tập B chứa số 1 nên phần bù sẽ không lấy số 1).
Để xác định tập hợp (A \ B) ∩ C, ta vẽ sơ đồ sau đây:

Từ sơ đồ, ta thấy (A \ B) ∩ C = [0; 1) (giao tức là lấy phần chung, tuy tập C có số 1 nhưng vì tập A \ B không lấy số 1 nên ta không lấy số 1).
Vậy ta chọn phương án B.
Câu 17. Cho A = {x ∈ ℝ | x + 2 ≥ 0}, B = {x ∈ ℝ | 5 – x ≥ 0}. Khi đó A \ B là:
A. [–2; 5];
B. [–2; 6];
C. (5; +∞);
D. (2; +∞).
Đáp án: C
Giải thích:
⦁ Ta có x + 2 ≥ 0.
Û x ≥ –2.
Do đó tập A = [–2; +∞).
⦁ Ta có 5 – x ≥ 0.
Û x ≤ 5.
Do đó tập B = (–∞; 5].
Để xác định tập hợp A \ B, ta vẽ sơ đồ sau đây:
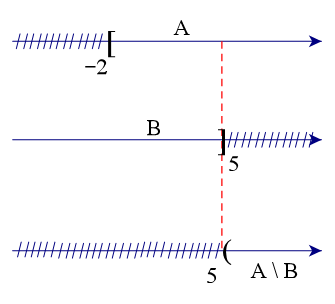
Từ sơ đồ, ta thấy A \ B = (5; +∞) (vì tập B có số 5 nên phần bù sẽ không lấy số 5).
Vậy ta chọn phương án C.
Câu 19. Cho hai tập khác rỗng A = (m – 1; 4], B = (–2; 2m + 2), m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.
A. –1 < m < 5;
B. 1 < m < 5;
C. –2 < m < 5;
D. m > –3.
Đáp án: C
Giải thích:
Vì tập A khác rỗng nên ta có m – 1 < 4.
Û m < 5 (1)
Vì tập B khác rỗng nên ta có –2 < 2m + 2.
Û –4 < 2m.
Û m > –2 (2)
Từ (1) và (2), ta suy ra tập hợp A và B đều khác rỗng khi và chỉ khi –2 < m < 5 (*).
Để A ∩ B ≠ ∅ thì m – 1 < 2m + 2.
Nghĩa là, m > –3 (**).
Giao (*) và (**) lại với nhau, ta thu được kết quả –2 < m < 5.
Vậy ta chọn phương án C.
Câu 20. Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
A. 54;
B. 40;
C. 26;
D. 68.
Đáp án: B
Giải thích:
Gọi T, L, K lần lượt là tập hợp các học sinh giỏi Toán, tập hợp các học sinh giỏi Lý và tập học các học sinh không giỏi môn nào cả.
Theo đề, ta có:
⦁ n(T) = 25;
⦁ n(L) = 23;
⦁ n(T ∩ L) = 14;
⦁ n(K) = 6.
Ta có sơ đồ Ven biểu diễn 3 tập hợp T, L, K như sau:
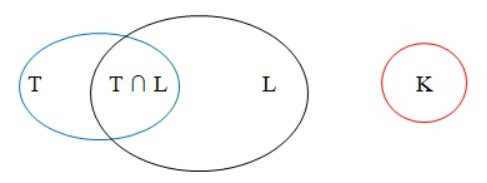
Khi đó số học sinh cả lớp là: n(T ∪ L) + n(K).
Ta có n(T ∪ L) = n(T) + n(L) – n(T ∩ L) = 25 + 23 – 14 = 34.
Vậy số học sinh cả lớp là: 34 + 6 = 40 (học sinh).
Do đó ta chọn phương án B.
Câu 21: Cho các tập hợp:
A = {m ∈ N | m là ước của 16}; B = {n ∈ N | n là ước của 24}.
Tập hợp A ∩ B là:
A. ∅
B. {1; 2; 4; 8}
C. {±1; ±2; ±4; ±8}
D. {1; 2; 4; 8; 16}
Ta có A = {m ∈ N | m là ước của 16} = {1; 2; 4; 8; 16},
B = {n ∈ N | n là ước của 24 = {1; 2; 3; 4; 6; 8; 12; 24}.
⇒ A ∩ B = {1; 2; 4; 8} .
Chú ý: A ∩ B chính là tập hợp các ước số tự nhiên của 8 = ƯCLN(16;24).
Chọn đáp án B
Câu 22: Gọi T là tập hợp các học sinh của lớp 10A; N là tập hợp các học sinh nam và G là tập hợp các học sinh nữ của lớp 10A. Xét các mệnh đề sau:
(I) N ∪ G = T
(II) N ∪ T = G
(III) N ∩ G = ∅
(IV) T ∩ G = N
(V) T \ N = G
(VI) N \ G = N .
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A. 2
B. 3
C. 4
D. 5
Trong các mệnh đề trên, có 4 mệnh đề đúng là (I), (III), (V), (VI).
Chú ý: Vì N ⊂ T, G ⊂ T nên N ∪ T = T, T ∩ G = G.
Chọn đáp án C
Câu 23: Xác định tập hợp X thỏa mãn hai điều kiện:
X ∪ {1; 2; 3} = {1; 2; 3; 4} và X ∩ {1; 2; 3; a} = {2; 3}.
A. X = {2; 3}
B. X = {1; 2; 3; 4}
C. X = {2; 3; 4}
D. X = {2; 3; 4; a}
Vì X ∪ {1; 2; 3} = {1; 2; 3; 4} nên 4 ∈ X và tập X ⊂ {1; 2; 3; 4}. Vì X ∩ {1; 2; 3; a} = 2; 3} nên 2; 3 ∈ X và 1 ∉ X, a ∉ X.
Tóm lại, ta có X = {2; 3; 4}.
Chọn đáp án C
Câu 24: Cho A = {a, b, c, d, e} và B = {c, d, e, k}. Tập hợp A ∩ B là:
A. {a, b}
B. {c, d, e}
C. {a, b, c, d, e, k}
D. {a, b, k}
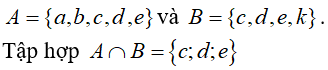
Chọn đáp án B
Câu 25: Cho hai tập hợp M = {1; 3; 6; 8} và N = {3; 6; 7; 9}. Tập hợp M ∪ N là:
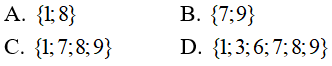
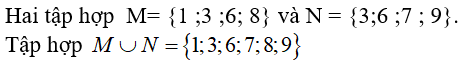
Chọn đáp án D
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.