Toán 12 (Kết nối tri thức) Bài 3: Đường tiệm cận của đồ thị hàm số

Mai Hương Ngày: 15-03-2024 Lớp 12

187

Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Kết nối tri thức) Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 3 từ đó học tốt môn Toán 12.

Toán 12 (Kết nối tri thức) Bài 3: Đường tiệm cận của đồ thị hàm số

Hoạt động 1 trang 20 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = \frac{2 x + 1}{x}$ có đồ thị (C). Với $x > 0$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = 2$ (H.1.19).

a) Tính khoảng cách MH.

b) Có nhận xét gì về khoảng cách MH khi $x \to + \infty$ ?

Lời giải:

a) Ta có: $M (x; \frac{2 x + 1}{x})$ ; $H (x; 2)$ .

Do đó, $M H = \sqrt{{(x - x)}^{2} + {(2 - \frac{2 x + 1}{x})}^{2}} = \sqrt{{(\frac{2 x - 2 x - 1}{x})}^{2}} = \frac{1}{x}$ (do $x > 0$ )

b) Ta có: $lim_{x \to + \infty} \frac{1}{x} = 0$ . Do đó, khi $x \to + \infty$ thì $M H \to 0$ .

Luyện tập 1 trang 21 SGK Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x - 1}{x - 1}$ .

Lời giải:

Ta có: $lim_{x \to + \infty} \frac{2 x - 1}{x - 1} = lim_{x \to + \infty} \frac{2 - \frac{1}{x}}{1 - \frac{1}{x}} = 2; lim_{x \to - \infty} \frac{2 x - 1}{x - 1} = lim_{x \to - \infty} \frac{2 - \frac{1}{x}}{1 - \frac{1}{x}} = 2$ .

Do đó, tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x - 1}{x - 1}$ là $y = 2$ .

Vận dụng 1 trang 21 SGK Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu.

Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số $m (t) = 15 e^{- 0, 012 t}$ . Khối lượng m(t) thay đổi ra sao khi $t \to + \infty$ ? Điều này thể hiện trên Hình 1.18 như thế nào?

Lời giải:

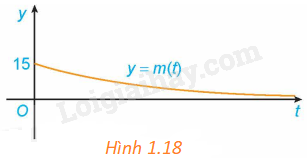
Ta có: $lim_{t \to + \infty} m (t) = lim_{t \to + \infty} 15 e^{- 0, 012 t} = lim_{t \to + \infty} \frac{15}{e^{0, 012 t}} = 0$

Do đó, $m (t) \to 0$ khi $t \to + \infty$ .

Trong hình 1.18, khi $t \to + \infty$ thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).

Hoạt động 2 trang 21 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = \frac{x}{x - 1}$ có đồ thị (C). Với $x > 1$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $x = 1$ (H.1.22).

a) Tính khoảng cách MH.

b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?

Lời giải:

a) Ta có: $M (x; \frac{x}{x - 1}); H (1; \frac{x}{x - 1})$

Do đó, $M H = \sqrt{{(1 - x)}^{2} + {(\frac{x}{x - 1} - \frac{x}{x - 1})}^{2}} = x - 1$ (do $x > 1$ )

b) Khi khoảng cách MH dần đến 0 thì tung độ của điểm M dần ra xa vô tận về phía trên (tung độ điểm M tiến ra $+ \infty$ ).

Luyện tập 2 trang 22 SGK Toán 12 Tập 1: Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ .

Lời giải:

Ta có: $lim_{x \to + \infty} \frac{2 x + 1}{x - 4} = lim_{x \to + \infty} \frac{2 + \frac{1}{x}}{1 - \frac{4}{x}} = 2; lim_{x \to - \infty} \frac{2 x + 1}{x - 4} = lim_{x \to - \infty} \frac{2 + \frac{1}{x}}{1 - \frac{4}{x}} = 2$ nên tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ là $y = 2$ .

Lại có: $lim_{x \to 4^{+}} f (x) = lim_{x \to 4^{+}} \frac{2 x + 1}{x - 4} = + \infty; lim_{x \to 4^{-}} f (x) = lim_{x \to 4^{-}} \frac{2 x + 1}{x - 4} = - \infty$ nên tiệm cận đứng của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ đường thẳng $x = 4$

Vận dụng 2 trang 22 SGK Toán 12 Tập 1: Để loại bỏ p% một loài tảo độc khỏi hồ nước, người ta ước tính chi phí bỏ ra là $C (p) = \frac{45 p}{100 - p}$ (triệu đồng), với $0 \leq p < 100$ . Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa của đường tiệm cận này.

Lời giải:

Ta có: $lim_{p \to 100^{-}} C (p) = lim_{p \to 100^{-}} \frac{45 p}{100 - p} = + \infty$ nên tiệm cận đứng của đồ thị hàm số C(p) là $p = 100$ .

Ý nghĩa của đường tiệm cận là: Không thể loại bỏ hết loài tảo độc ra khỏi hồ nước dù chi phí là bao nhiêu.

Hoạt động 3 trang 23 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = x - 1 + \frac{2}{x + 1}$ có đồ thị (C) và đường thẳng $y = x - 1$ như Hình 1.24.

a) Với $x > - 1$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = x - 1$ . Có nhận xét gì về khoảng cách MH khi $x \to + \infty$ ?

b) Chứng tỏ rằng $lim_{x \to + \infty} [f (x) - (x - 1)] = 0$ . Tính chất này thể hiện trên Hình 1.24 như thế nào?

Lời giải:

a) Nhìn vào đồ thị ta thấy, khi $x \to + \infty$ thì khoảng cách MH tiến tới 0.

b) Ta có: $lim_{x \to + \infty} [f (x) - (x - 1)] = lim_{x \to + \infty} [x - 1 + \frac{2}{x + 1} - (x - 1)] = lim_{x \to + \infty} \frac{2}{x + 1} = lim_{x \to + \infty} \frac{\frac{2}{x}}{1 + \frac{1}{x}} = 0$

Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng $y = x - 1$ tiến đến 0 khi $x \to + \infty$ .

Luyện tập 3 trang 24 SGK Toán 12 Tập 1: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{x^{2} - 4 x + 2}{1 - x}$ .

Lời giải:

Ta có: $lim_{x \to 1^{+}} f (x) = lim_{x \to 1^{+}} \frac{x^{2} - 4 x + 2}{1 - x} = + \infty$ ; $lim_{x \to 1^{-}} f (x) = lim_{x \to 1^{-}} \frac{x^{2} - 4 x + 2}{1 - x} = - \infty$

Vậy tiệm cận đứng của đồ thị hàm số $y = f (x)$ là đường thẳng $x = 1$

Ta có: $y = f (x) = \frac{x^{2} - 4 x + 2}{1 - x} = - x + 3 - \frac{1}{1 - x}$

Do đó, $lim_{x \to + \infty} [f (x) - (- x + 3)] = lim_{x \to + \infty} \frac{- 1}{1 - x} = 0$ , $lim_{x \to - \infty} [f (x) - (- x + 3)] = lim_{x \to - \infty} \frac{- 1}{1 - x} = 0$

Vậy tiệm cận xiên của đồ thị hàm số $y = f (x)$ là đường thẳng $y = - x + 3$

Bài 1.16 trang 25 SGK Toán 12 Tập 1: Hình 1.26 là đồ thị của hàm số $y = f (x) = \frac{2 x^{2}}{x^{2} - 1}$

Sử dụng đồ thị này, hãy:
a) Viết kết quả của các giới hạn sau: $lim_{x \to - \infty} f (x)$ ; $lim_{x \to + \infty} f (x)$ ; $lim_{x \to 1^{-}} f (x)$ ; $lim_{x \to - 1^{+}} f (x)$
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

Lời giải:

a) $lim_{x \to - \infty} f (x) = 2$ ; $lim_{x \to + \infty} f (x) = 2$ ; $lim_{x \to 1^{-}} f (x) = - \infty$ ; $lim_{x \to - 1^{+}} f (x) = - \infty$

b) Do đó, tiệm cận đứng của đồ thị hàm số là $x = 1; x = - 1$ .

Tiệm cận ngang của đồ thị hàm số là $y = 2$

Bài 1.17 trang 25 SGK Toán 12 Tập 1: Đường thẳng $x = 1$ có phải là tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} + 2 x - 3}{x - 1}$ không?

Lời giải:

Ta có: $lim_{x \to 1^{+}} f (x) = lim_{x \to 1^{+}} \frac{x^{2} + 2 x - 3}{x - 1} = lim_{x \to 1^{+}} \frac{(x - 1) (x + 3)}{x - 1} = lim_{x \to 1^{+}} (x + 3) = 4$

$lim_{x \to 1^{-}} f (x) = lim_{x \to 1^{-}} \frac{x^{2} + 2 x - 3}{x - 1} = lim_{x \to 1^{-}} \frac{(x - 1) (x + 3)}{x - 1} = lim_{x \to 1^{-}} (x + 3) = 4$

Do đó, đường thẳng $x = 1$ không là tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} + 2 x - 3}{x - 1}$ .

Bài 1.18 trang 25 SGK Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:
a) $y = \frac{3 - x}{2 x + 1}$ ;
b) $y = \frac{2 x^{2} + x - 1}{x + 2}$ .

Lời giải:

a) Vì $lim_{x \to + \infty} y = lim_{x \to + \infty} \frac{3 - x}{2 x + 1} = lim_{x \to + \infty} \frac{\frac{3}{x} - 1}{2 + \frac{1}{x}} = - \frac{1}{2}$ ; $lim_{x \to - \infty} y = lim_{x \to - \infty} \frac{3 - x}{2 x + 1} = lim_{x \to - \infty} \frac{\frac{3}{x} - 1}{2 + \frac{1}{x}} = - \frac{1}{2}$

Do đó, đường thẳng $y = \frac{- 1}{2}$ là tiệm cận ngang của đồ thị hàm số $y = \frac{3 - x}{2 x + 1}$ .

Vì $lim_{x \to {(- \frac{1}{2})}^{-}} y = lim_{x \to {(- \frac{1}{2})}^{-}} \frac{3 - x}{2 x + 1} = - \infty; lim_{x \to {(- \frac{1}{2})}^{+}} y = lim_{x \to {(- \frac{1}{2})}^{+}} \frac{3 - x}{2 x + 1} = + \infty$

Do đó, đường thẳng $x = \frac{- 1}{2}$ là tiệm cận đứng của đồ thị hàm số $y = \frac{3 - x}{2 x + 1}$ .

b) Vì $lim_{x \to - \infty} y = lim_{x \to - \infty} \frac{2 x^{2} + x - 1}{x + 2} = lim_{x \to - \infty} [x \frac{(2 + \frac{1}{x} - \frac{1}{x^{2}})}{(1 + \frac{2}{x})}] = - \infty$

$lim_{x \to + \infty} y = lim_{x \to + \infty} \frac{2 x^{2} + x - 1}{x + 2} = lim_{x \to + \infty} [x \frac{(2 + \frac{1}{x} - \frac{1}{x^{2}})}{(1 + \frac{2}{x})}] = + \infty$

Do đó, đồ thị hàm số $y = \frac{2 x^{2} + x - 1}{x + 2}$ không có tiệm cận ngang.

Vì $lim_{x \to - 2^{-}} y = lim_{x \to - 2^{-}} \frac{2 x^{2} + x - 1}{x + 2} = - \infty; lim_{x \to - 2^{+}} y = lim_{x \to - 2^{+}} \frac{2 x^{2} + x - 1}{x + 2} = + \infty$

Do đó, đồ thị hàm số $y = \frac{2 x^{2} + x - 1}{x + 2}$ có tiệm cận đứng là $x = - 2$

Ta có: $y = \frac{2 x^{2} + x - 1}{x + 2} = 2 x - 3 + \frac{5}{x + 2}$

$lim_{x \to + \infty} [f (x) - (2 x - 3)] = lim_{x \to + \infty} [2 x - 3 + \frac{5}{x + 2} - (2 x - 3)] = lim_{x \to + \infty} \frac{5}{x + 2} = 0$

$lim_{x \to - \infty} [f (x) - (2 x - 3)] = lim_{x \to - \infty} [2 x - 3 + \frac{5}{x + 2} - (2 x - 3)] = lim_{x \to - \infty} \frac{5}{x + 2} = 0$

Do đó, đồ thị hàm số $y = \frac{2 x^{2} + x - 1}{x + 2}$ có tiệm cận xiên là: $y = 2 x - 3$ .

Bài 1.19 trang 25 SGK Toán 12 Tập 1: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là $C (x) = 2 x + 50$ (triệu đồng). Khi đó, $f (x) = \frac{C (x)}{x}$ là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và $lim_{x \to + \infty} f (x) = 2$ . Tính chất này nói lên điều gì?

Lời giải:

Ta có: $f (x) = \frac{C (x)}{x} = \frac{2 x + 50}{x}$

Vì $f^{'} (x) = \frac{- 50}{x^{2}} < 0$ với mọi số thực x nên hàm số $f (x) = \frac{C (x)}{x}$ giảm.

$lim_{x \to + \infty} f (x) = lim_{x \to + \infty} \frac{2 x + 50}{x} = lim_{x \to + \infty} \frac{2 + \frac{50}{x}}{1} = 2$ (đpcm)

Bài 1.20 trang 25 SGK Toán 12 Tập 1: Một mảnh vườn hình chữ nhật có diện tích bằng $144 m^{2}$ . Biết độ dài một cạnh của mảnh vườn là x (m).

a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.

b) Tìm các tiệm cận của đồ thị hàm số P(x).

Lời giải:

a) Độ dài cạnh còn lại của mảnh vườn là: $\frac{144}{x} (m)$

Chu vi của mảnh vườn là: $P (x) = 2 (x + \frac{144}{x}) = 2 x + \frac{288}{x} (m)$

b) Vì $lim_{x \to + \infty} P (x) = lim_{x \to + \infty} (2 x + \frac{288}{x}) = + \infty$ ; $lim_{x \to - \infty} P (x) = lim_{x \to - \infty} (2 x + \frac{288}{x}) = - \infty$

Do đó, đồ thị hàm số P(x) không có tiệm cận ngang.

Vì $lim_{x \to 0^{-}} y = lim_{x \to 0^{-}} (2 x + \frac{288}{x}) = - \infty; lim_{x \to 0^{+}} y = lim_{x \to 0^{+}} (2 x + \frac{288}{x}) = + \infty$