Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 1 từ đó học tốt môn Toán 12.
Nội dung bài viết
Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số
Hoạt động 1 trang 6 SGK Toán 12 Tập 1: Quan sát đồ thị của hàm số y=x2 (H.1.2)
a) Hàm số đồng biến trên khoảng nào?
b) Hàm số nghịch biến trên khoảng nào?
Lời giải:
Từ đồ thị ta thấy:
+ Xét khoảng (0;+∞): ∀x1,x2∈(0;+∞),x1<x2 thì x21<x22 hay f(x1)<f(x2).
Suy ra, hàm số y=x2 đồng biến trên (0;+∞).
+ Xét khoảng (−∞;0): ∀x1,x2∈(−∞;0),x1<x2 thì x21>x22hay f(x1)>f(x2).
Suy ra, hàm số y=x2 nghịch biến trên (−∞;0).
Lời giải:
Tập xác định của hàm số là R.
Trong khoảng (−∞;0) và (2;+∞) thì đồ thị hàm số y=x3−3x2+2 đi lên từ trái sang phải nên hàm số y=x3−3x2+2 đồng biến trên khoảng (−∞;0) và (2;+∞).
Trong khoảng (0;2) thì đồ thị hàm số y=x3−3x2+2 đi xuống từ trái sang phải nên hàm số y=x3−3x2+2 nghịch biến trên khoảng (0;2).
Hoạt động 2 trang 6 SGK Toán 12 Tập 1: 
b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng (−1;1)?
Lời giải:
a) + Xét khoảng (−∞;−1) ta có: y′=(−x)′=−1<0
Trong khoảng (−∞;−1) ta thấy hàm số y nghịch biến và đạo hàm y′<0.
+ Xét khoảng (1;+∞) ta có: y′=x′=1>0
Trong khoảng (1;+∞) ta thấy hàm số y đồng biến và đạo hàm y′>0.
b) Trong khoảng (−1;1) ta có: y′=(1)′=0
Trong khoảng (−1;1) ta thấy hàm số y không đổi và đạo hàm y′=0.
Lời giải:
Tập xác định của hàm số là R.
Ta có: y′=−2x+2,y′>0 với x∈(−∞;1); y<0 với x∈(1;+∞).
Do đó, hàm số đồng biến trên khoảng (−∞;1) và nghịch biến trên khoảng (1;+∞).
Hoạt động 3 trang 7 SGK Toán 12 Tập 1: Cho hàm số y=f(x)=x3−3x2+2x+1.
a) Tính đạo hàm f′(x) và tìm các điểm x mà f′(x)=0.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
a) f′(x)=(x3−3x2+2x+1)′=3x2−6x+2
f′(x)=0⇔3x2−6x+2=0⇔[x=3−√33x=3+√33
Vậy x=3−√33,x=3+√33 thì f′(x)=0
b) Bảng biến thiên:
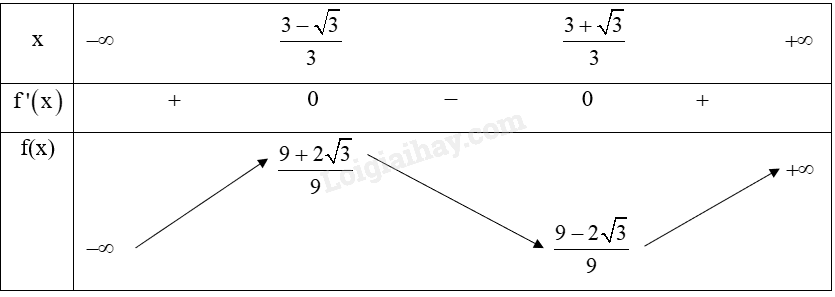
c) Hàm số y=f(x)=x3−3x2+2x+1 đồng biến trên khoảng (−∞;3−√33) và (3+√33;+∞).
Hàm số y=f(x)=x3−3x2+2x+1 nghịch biến trên khoảng (3−√33;3+√33).
Luyện tập 3 trang 9 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:
Lời giải:
a) Tập xác định: D=R.
Ta có: y′=x2+6x+5,y′=0⇔x2+6x+5=0⇔[x=−1x=−5
Lập bảng biến thiên của hàm số:
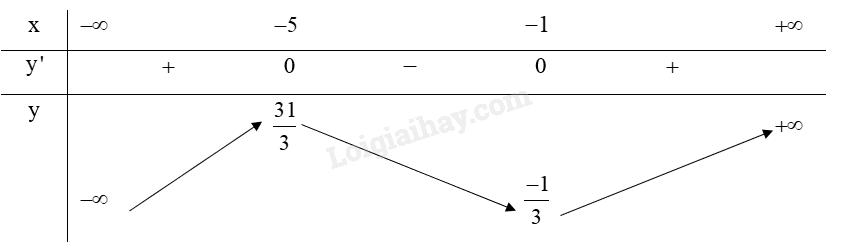
Hàm số y=13x3+3x2+5x+2 đồng biến trên khoảng (−∞;−5) và (−1;+∞).
Hàm số y=13x3+3x2+5x+2 nghịch biến trên khoảng (−5;−1).
b) Tập xác định: D=R∖{2}.
Ta có: y′=(−2x+5)(x−2)−(−x2+5x−7)(x−2)2=−x2+4x−3(x−2)2
y′=0⇔[x=3x=1 (thỏa mãn)
Lập bảng biến thiên của hàm số:
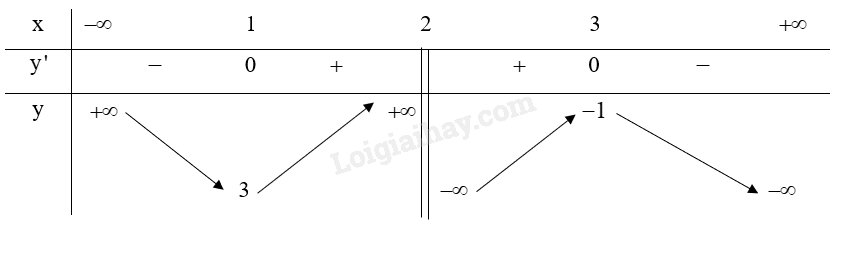 Hàm số y=−x2+5x−7x−2 đồng biến trên khoảng (1;2) và (2;3).
Hàm số y=−x2+5x−7x−2 đồng biến trên khoảng (1;2) và (2;3).
Hàm số y=−x2+5x−7x−2 nghịch biến trên khoảng (−∞;1) và (3;+∞).
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).
b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.

Lời giải:
a) Ta có: v(t)=s′(t)=(t3−9t2+15t)′=3t2−18t+15
b) Tập xác định: D=R.
Ta có:v(t)>0⇔3t2−18t+15>0⇔(t−1)(t−5)>0⇔[t<1t>5
v(t)<0⇔3t2−18t+15<0⇔(t−1)(t−5)<0⇔1<t<5
Chất điểm chuyển động theo chiều dương (sang bên phải) khi v(t)>0, tức là t∈(−∞;1)∪(5;+∞).
Chất điểm chuyển động theo chiều âm (sang bên trái) khi v(t)<0, tức là 1<t<5.
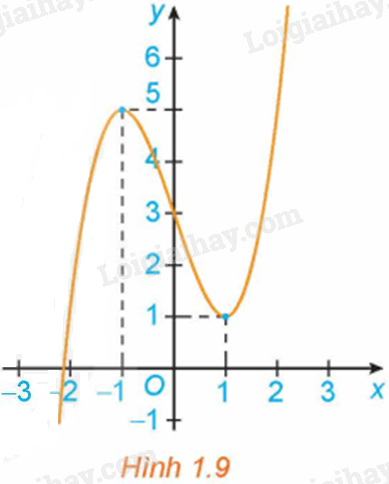
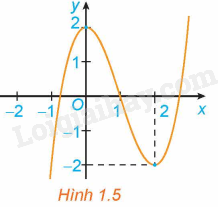
Lời giải:
Từ đồ thị hàm số, ta có:
Hàm số đạt cực tiểu tại x=1 và yCT=y(1)=1.
Hàm số đạt cực đại tại x=−1 và yCD=y(−1)=5
Hoạt động 5 trang 10 SGK Toán 12 Tập 1: Cho hàm số y=13x3−3x2+8x+1.
a) Tính đạo hàm f′(x) và tìm các điểm mà tại đó đạo hàm f′(x) bằng 0.
b) Lập bảng biến thiên của hàm số.
c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.
Lời giải:
a) Tập xác định: D=R.
y′=x2−6x+8, y′=0⇔x2−6x+8=0⇔[x=4x=2
Vậy x=4;x=2 thì f′(x)=0
b) Bảng biến thiên:
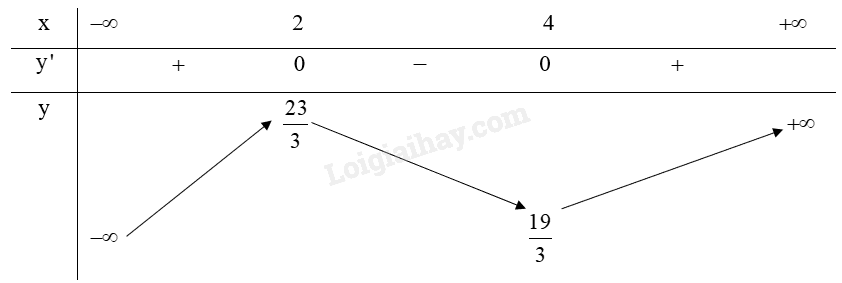
c) Từ bảng biến thiên ta có:
Hàm số y=13x3−3x2+8x+1 có điểm cực đại là (2;233).
Hàm số y=13x3−3x2+8x+1 có điểm cực tiểu là (4;193).
Lời giải:
Giả sử hàm số y=f(x) liên tục trên khoảng (a; b) chứa điểm x0 và có đạo hàm trên các khoảng (a;x0) và (x0;b). Nếu f’(x) không đổi dấu qua x0 thì:
TH1: f′(x)<0 với mọi x∈(a;x0) và f′(x)<0 với mọi x∈(x0;b), ta có bảng biến thiên:
Giả sử hàm số y=f(x) liên tục trên khoảng (a; b) chứa điểm x0 và có đạo hàm trên các khoảng (a;x0) và (x0;b). Nếu f’(x) không đổi dấu qua x0 thì:
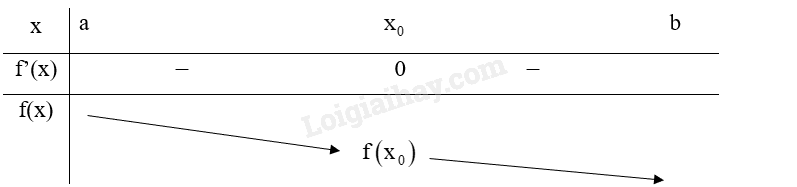
TH1: f′(x)<0 với mọi x∈(a;x0) và f′(x)<0 với mọi x∈(x0;b), ta có bảng biến thiên:

Do đó, x0 không phải là điểm cực trị của hàm số f(x).
Luyện tập 5 trang 12 SGK Toán 12 Tập 1: Tìm cực trị của các hàm số sau:
Lời giải:
a) Tập xác định của hàm số là R.
Ta có: y′=4x3−6x,y′=0⇔4x3−6x=0⇔[x=0x=±√62;
Bảng biến thiên:
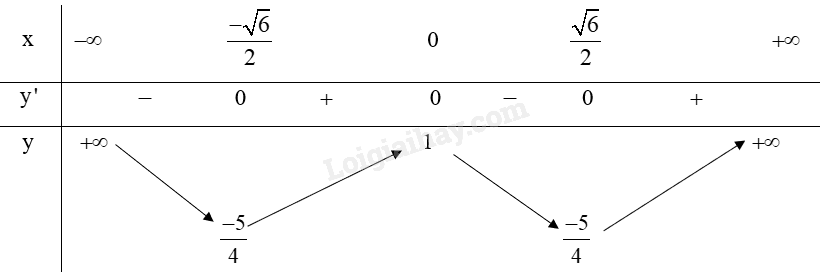
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại x=0 và .
Hàm số đạt cực tiểu tại x=±√62 và yCT=−54.
b) Tập xác định: D=R∖{−2}.
Ta có: y′=(−2x+2)(x+2)−(−x2+2x−1)(x+2)2=−x2−4x+5(x+2)2
y′=0⇔[x=−5x=1 (thỏa mãn)
Lập bảng biến thiên của hàm số:
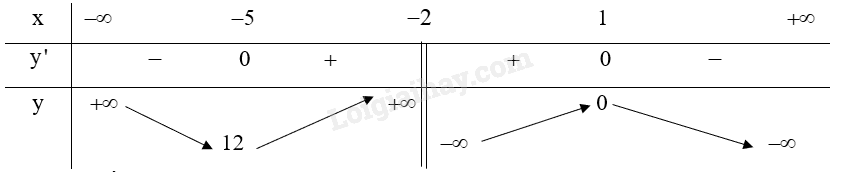
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại x=1 và .
Hàm số đạt cực tiểu tại x=−5 và yCT=12.
Lời giải:
Xét hàm số: h(t)=2+24,5t−4,9t2.
Tập xác định của hàm số là R.
Ta có:h′(t)=−9,8t+24,5;h′(t)=0⇔−9,8t+24,5=0⇔t=52.
Bảng biến thiên:
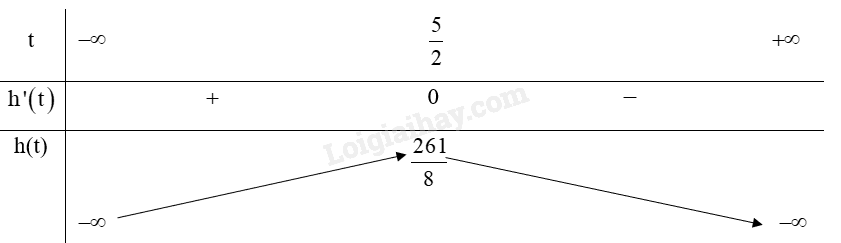
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại t=52,
Vậy thời điểm vật đạt độ cao lớn nhất là t=52 giây
a) Đồ thị hàm số y=x3−32x2 (H.1.11);
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số y=x3−32x2 (H.1.11);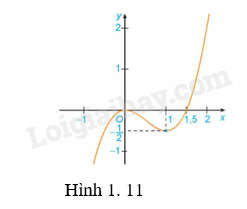
b) Đồ thị hàm số y=3√(x2−4)2 (H.1.12).

Lời giải:
a) Hàm số y=x3−32x2 đồng biến trên (−∞;0) và (1;+∞).
Hàm số y=x3−32x2 nghịch biến trên (0;1).
b) Hàm số y=3√(x2−4)2 đồng biến trên (−2;0) và (2;+∞).
Hàm số y=3√(x2−4)2 nghịch biến trên (−∞;−2) và (0;2).
Lời giải:
a) Tập xác định: D=R.
Ta có: y′=x2−4x+3,y′=0⇔x2−4x+3=0⇔[x=3x=1
Lập bảng biến thiên của hàm số:

Hàm số y=13x3−2x2+3x+1 đồng biến trên khoảng (−∞;1) và (3;+∞).
Hàm số y=13x3−2x2+3x+1 nghịch biến trên khoảng (1;3).
b) Tập xác định: D=R.
Ta có: y′=−3x2+4x−5
Vì−3x2+4x−5=−3(x2−2.23+49)−113=−3(x−23)2−113<0∀x∈R
Do đó, y′<0∀x∈R.
Vậy hàm số y=−x3+2x2−5x+3 nghịch biến trên (−∞;+∞)
Bài 1.3 trang 13 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:
Lời giải:
a) Tập xác định: D=R∖{−2}.
Ta có: y′=2(x+2)−(2x−1)(x+2)2=2x+4−2x+1(x+2)2=5(x+2)>0∀x≠−2
Do đó, hàm số y=2x−1x+2 đồng biến trên (−∞;−2) và (−2;+∞).
b) Tập xác định: D=R∖{3}.
Ta có:y′=(x2+x+4)′(x−3)−(x2+x+4)(x−3)′(x−3)2=(2x+1)(x−3)−x2−x−4(x−3)2=x2−6x−7(x−3)2
y′=0⇔x2−6x−7(x−3)2=0⇔[x=7x=−1 (thỏa mãn)
Lập bảng biến thiên của hàm số:
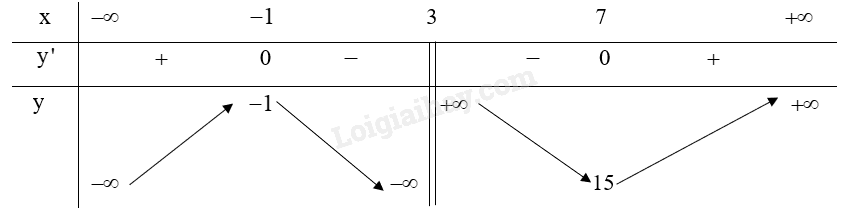
Từ bảng biến thiên ta thấy:
Hàm số y=x2+x+4x−3 nghịch biến trên khoảng (−1;3) và (3;7).
Hàm số y=x2+x+4x−3 đồng biến trên khoảng (−∞;−1) và (7;+∞).
Lời giải:
a) Tập xác định: D=[−2;2].
Ta có: y′=(4−x2)′2√4−x2=−x√4−x2,y′=0⇔x=0(tm)
Lập bảng biến thiên của hàm số:

Hàm số y=√4−x2 đồng biến trên khoảng (−2;0).
Hàm số y=√4−x2 nghịch biến trên khoảng (0;2).
b) Tập xác định: D=R.
Ta có:y′=(x2+1)−2x.x(x2+1)2=x2+1−2x2(x2+1)2=−x2+1(x2+1)2,y′=0⇔−x2+1(x2+1)2=0⇔[x=1x=−1
Lập bảng biến thiên của hàm số:
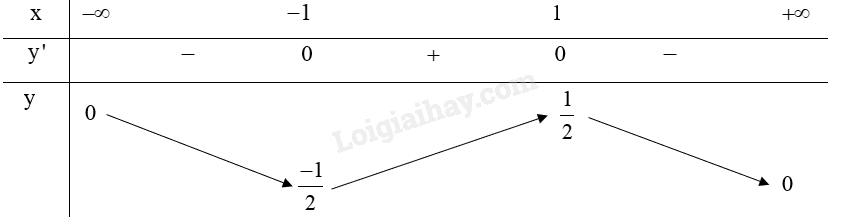
Hàm số y=xx2+1 nghịch biến trên khoảng (−∞;−1), (1;+∞).
Hàm số y=xx2+1 đồng biến trên khoảng (−1;1).
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và limt→+∞N(t). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Lời giải:
a) Dân số của thị trấn đó vào năm 2000 là: N(0)=25.0+100+5=105=2 (nghìn người)
Dân số của thị trấn đó vào năm 2015 là: N(15)=25.15+1015+5=19,25 (nghìn người)
b) Ta có: , limt→+∞N(t)=limt→+∞25t+10t+5=limt→+∞25+10t1+5t=25
Vì limt→+∞N(t)=25 và nên dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua ngưỡng 25 nghìn người.
a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.
b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.
Lời giải:
a) Vì f′(x)>0 khi x∈(2;4) và x∈(6;+∞). Do đó, hàm số f(x) đồng biến trên (2;4) và (6;+∞).
Vì f′(x)<0 khi x∈(0;2) và x∈(4;6). Do đó, hàm số f(x) nghịch biến trên (0;2) và (4;6).
b) Vì f′(x)<0 với mọi x∈(0;2) và f′(x)>0 với mọi x∈(2;4) thì x=2 là một điểm cực tiểu của hàm số f(x).
Vì f′(x)>0 với mọi x∈(2;4) và f′(x)<0 với mọi x∈(4;6) thì điểm x=4 là một điểm cực đại của hàm số f(x).
Vì f′(x)<0 với mọi x∈(4;6) và f′(x)>0 với mọi x∈(6;+∞) thì điểm x=6 là một điểm cực tiểu của hàm số f(x).
a) y=2x3−9x2+12x−5;y=x4−4x2+2
b) ;
c) y=x2−2x+3x−1;
d) y=√4x−2x2
Lời giải:
a) Tập xác định: D=R.
y′=6x2−18x+12, y′=0⇔6x2−18x+12=0⇔[x=1x=2
Bảng biến thiên:

Từ bảng biến thiên ta có:
Hàm số y=2x3−9x2+12x−5 có điểm cực đại là (1;0).
Hàm số y=2x3−9x2+12x−5 có điểm cực tiểu là (2;−1).
b) Tập xác định của hàm số là R.
Ta có: y′=4x3−8x,y′=0⇔4x3−8x=0⇔[x=0x=±√2
Bảng biến thiên:

Từ bảng biến thiên ta có:
Hàm số y=x4−4x2+2 đạt cực đại tại x=0 và .
Hàm số y=x4−4x2+2 đạt cực tiểu tại x=±√2 và yCT=−2.
c) Tập xác định: D=R∖{1}.
Ta có: y′=(2x−2)(x−1)−(x2−2x+3)(x−1)2=x2−2x−1(x−1)2
y′=0⇔[x=1−√2x=1+√2 (thỏa mãn)
Lập bảng biến thiên của hàm số:
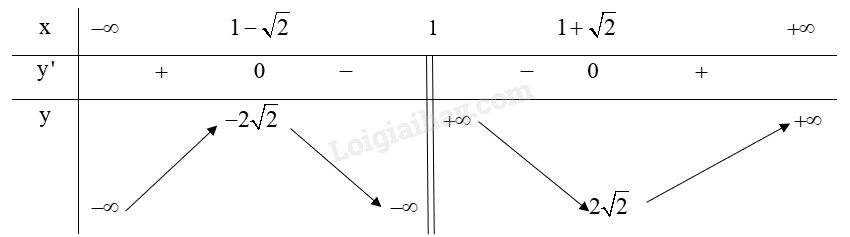
Từ bảng biến thiên ta có:
Hàm số y=x2−2x+3x−1 đạt cực đại tại x=1−√2 và .
Hàm số y=x2−2x+3x−1 đạt cực tiểu tại x=1+√2 và yCT=2√2.
d) y=√4x−2x2
Tập xác định: D=[0;2].
Ta có: y′=(4x−2x2)′2√4x−2x2=−x+1√4x−2x2,y′=0⇔x=1(tm)
Ta có bảng biến thiên của hàm số:
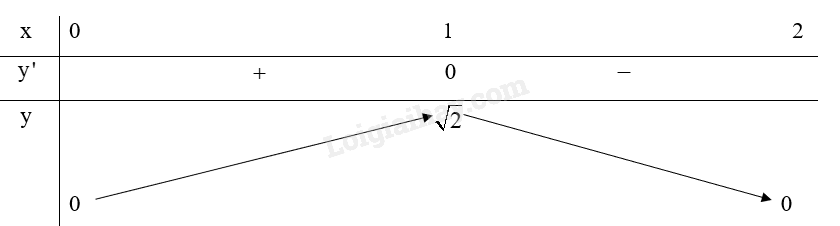
Do đó, hàm số đạt cực đại tại x=1, , hàm số không có cực tiểu.
a) Tính các giới hạn limx→0+f(x)−f(0)x−0 và limx→0−f(x)−f(0)x−0. Từ đó suy ra hàm số không có đạo hàm tại x=0.
b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại x=0. (Xem Hình 1.4)
Lời giải:
a) limx→0+f(x)−f(0)x−0=limx→0+|x|−0x−0=limx→0+xx=1
limx→0−f(x)−f(0)x−0=limx→0−|x|−0x−0=limx→0−−xx=−1
Vì limx→0+f(x)−f(0)x−0≠limx→0−f(x)−f(0)x−0 nên hàm số không có đạo hàm tại x=0.
b) Đồ thị hàm số y=f(x)=|x|:
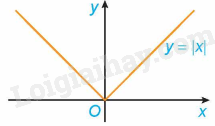
Ta có: y=f(x)=|x|={−xkhix∈(−∞;0)xkhix∈(0;+∞)
Hàm số y=f(x)=|x| liên tục và xác định trên (−∞;+∞)
Với số h>0 ta có: Với x∈(−h;h)⊂(−∞;+∞) và x≠0 thì y=f(x)=|x|>0=f(0)
Do đó, hàm số y=f(x)=|x| có cực tiểu là x=0.
Lời giải:
Ta có: f′(t)=−5000(1+5e−t)′(1+5e−t)2=25000e−t(1+5e−t)2
Tốc độ bán hàng là lớn nhất khi f′(t) lớn nhất.
Đặt h(t)=25000e−t(1+5e−t)2.
h′(t)=−25000e−t(1+5e−t)2−2.(−5e−t).(1+5e−t).25000e−t(1+5e−t)4
=−25000e−t(1+5e−t)(1+5e−t−10e−t)(1+5e−t)4=−25000e−t(1−5e−t)(1+5e−t)3
h′(t)=0⇔−25000e−t(1−5e−t)(1+5e−t)3=0⇔1−5e−t=0⇔e−t=15⇔t=ln5(tm)
Ta có bảng biến thiên với t∈[0;+∞):
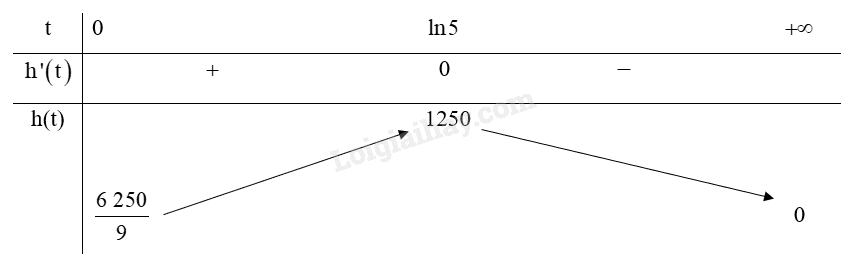
Vậy sau khi phát hành khoảng ln5≈1,6 năm thì thì tốc độ bán hàng là lớn nhất.
Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.