Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Mai Hương Ngày: 14-03-2024 Lớp 12

289

Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 2 từ đó học tốt môn Toán 12.

Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Hoạt động 1 trang 15 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = x^{2} - 2 x$ với $x \in [0; 3]$ , có đồ thị như Hình 1.15.

a) Giá trị lớn nhất M của hàm số trên đoạn $[0; 3]$ là bao nhiêu? Tìm $x_{0}$ sao cho $f (x_{0}) = M$ .

b) Giá trị nhỏ nhất m của hàm số trên đoạn $[0; 3]$ là bao nhiêu? Tìm $x_{0}$ sao cho $f (x_{0}) = m$ .

Lời giải:

a) Giá trị lớn nhất của đồ thị hàm số trên đoạn $[0; 3]$ là $M = 3$ .

Với $x_{0} = 3$ thì $f (3) = 3$ .

b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn $[0; 3]$ là $m = - 1$ .

Với $x_{0} = 1$ thì $f (1) = - 1$ .

Luyện tập 1 trang 17 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = \sqrt{2 x - x^{2}}$ ;

b) $y = - x + \frac{1}{x - 1}$ trên khoảng $(1; + \infty)$ .

Lời giải:

a) Tập xác định của hàm số là $[0; 2]$ .

Với $x \in [0; 2]$ ta có: $y^{'} = \frac{{(2 x - x^{2})}^{'}}{2 \sqrt{2 x - x^{2}}} = \frac{- x + 1}{\sqrt{2 x - x^{2}}}$ , $y^{'} = 0 \Leftrightarrow \frac{- x + 1}{\sqrt{2 x - x^{2}}} = 0 \Leftrightarrow x = 1 (t m)$

Lập bảng biến thiên của hàm số trên đoạn $[0; 2]$ :

Từ bảng biến thiên ta thấy: $min_{[- 1; 1]} f (x) = f (0) = f (2) = 0, max_{[- 1; 1]} f (x) = f (1) = 1$ .

b) Với $x \in (1; + \infty)$ ta có:

Ta có: $y^{'} = - 1 + \frac{- 1}{{(x - 1)}^{2}} < 0 \forall x \in (1; + \infty)$

$lim_{x \to 1^{+}} y = lim_{x \to 1^{+}} (- x + \frac{1}{x - 1}) = + \infty; lim_{x \to + \infty} y = lim_{x \to + \infty} (- x + \frac{1}{x - 1}) = - \infty$

Lập bảng biến thiên của hàm số trên $(1; + \infty)$ :

Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên $(1; + \infty)$ .

Hoạt động 2 trang 17 SGK Toán 12 Tập 1: Xét hàm số $y = f (x) = x^{3} - 2 x^{2} + 1$ trên đoạn $[- 1; 2]$ , với đồ thị như Hình 1.16.

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $[- 1; 2]$ .

b) Tính đạo hàm f’(x) và tìm các điểm $x \in (- 1; 2)$ mà $f^{'} (x) = 0$ .

c) Tính giá trị của hàm số tại hai đầu mút của đoạn $[- 1; 2]$ và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với $min_{[- 1; 2]} f (x)$ , số lớn nhất trong các giá trị này với $max_{[- 1; 2]} f (x)$ .

Lời giải:

a) Nhìn vào đồ thị ta thấy, trên đoạn $[- 1; 2]$ ta có:

+ Giá trị lớn nhất của hàm số là $max_{[- 1; 2]} f (x) = f (0) = f (2) = 1$ .

+ Giá trị nhỏ nhất của hàm số là $min_{[- 1; 2]} f (x) = f (- 1) = - 2$ .

b) $f^{'} (x) = 3 x^{2} - 4 x, f^{'} (x) = 0 \Leftrightarrow 3 x^{2} - 4 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \frac{4}{3} \end{array}$

Vậy $x = 0, x = \frac{4}{3}$ thì $f^{'} (x) = 0$ .

c) Ta có: $f (0) = 1; f (\frac{4}{3}) = {(\frac{4}{3})}^{3} - 2. {(\frac{4}{3})}^{2} + 1 = \frac{- 5}{27}; f (- 1) = {(- 1)}^{3} - 2. {(- 1)}^{2} + 1 = - 2$ ;

$f (2) = 2^{3} - {2.2}^{2} + 1 = 1$

Do đó, số nhỏ nhất trong các giá trị này là $- 2$ , số lớn nhất trong các giá trị này là 1.

Ta thấy: $max_{[- 1; 2]} f (x) = 1$ , $min_{[- 1; 2]} f (x) = - 2$ .

Luyện tập 2 trang 18 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) $y = 2 x^{3} - 3 x^{2} + 5 x + 2$ trên đoạn $[0; 2]$ ;

b) $y = (x + 1) e^{- x}$ trên đoạn $[- 1; 1]$ .

Lời giải:

a) Ta có: $y^{'} = 6 x^{2} - 6 x + 5 = 6 (x^{2} - x + \frac{5}{6}) = 6 {(x - \frac{1}{2})}^{2} + \frac{7}{2} > 0 \forall x \in [0; 2]$

Do đó, hàm số $y = 2 x^{3} - 3 x^{2} + 5 x + 2$ đồng biến trên $[0; 2]$ .

Ta có: $y (0) = 2; y (2) = {2.2}^{3} - {3.2}^{2} + 5.2 + 2 = 16$

Do đó, $max_{[0; 2]} y = y (2) = 16, min_{[0; 2]} y = y (0) = 2$

b) Ta có: $y^{'} = e^{- x} - (x + 1) e^{- x} = e^{- x} (1 - x - 1) = - x . e^{- x}$

$y^{'} = 0 \Leftrightarrow - x . e^{- x} = 0 \Leftrightarrow x = 0$ (thỏa mãn $x \in [- 1; 1]$ )

$y (- 1) = 0; y (0) = 1; y (1) = \frac{2}{e}$

Do đó, $max_{[- 1; 1]} y = y (0) = 1, min_{[- 1; 1]} y = y (- 1) = 0$

Vận dụng trang 18 SGK Toán 12 Tập 1: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số $N (t) = - t^{3} + 12 t^{2}, 0 \leq t \leq 12,$ trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).

a) Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.

b) Đạo hàm N’(t) biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?

Lời giải:

a) Với $0 \leq t \leq 12$ ta có:

$N^{'} (t) = - 3 t^{2} + 24 t, N^{'} (t) = 0 \Leftrightarrow - 3 t^{2} + 24 t = 0 \Leftrightarrow [\begin{array}{l} t = 0 (t m) \\ t = 8 (t m) \end{array}$

Ta có: $N (0) = 0, N (8) = - 8^{3} + {12.8}^{2} = 256, N (12) = - 12^{3} + {12.12}^{2} = 0$

Do đó, số người tối đa bị nhiễm bệnh ở địa phương là 256 người trong 12 tuần đầu.

b) Hàm số biểu thị tốc độ độ lây lan của virus là: $N^{'} (t) = - 3 t^{2} + 24 t$

Đặt $f (t) = - 3 t^{2} + 24 t$ , với $0 \leq t \leq 12$

Ta có: $f^{'} (t) = - 6 t + 24, f^{'} (t) = 0 \Leftrightarrow t = 4 (t m)$

$f (0) = 0, f (4) = - {3.4}^{2} + 24.4 = 48, f (12) = - {3.12}^{2} + 24.12 = - 144$

Do đó, virus sẽ lây lan nhanh nhất khi $t = 4$ (tuần thứ 4).

Bài 1.10 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = - x^{2} + 4 x + 3$ ;
b) $y = x^{3} - 2 x^{2} + 1$ trên $[0; + \infty)$ ;
c) $y = \frac{x^{2} - 2 x + 3}{x - 1}$ trên $(1; + \infty)$ ;
d) $y = \sqrt{4 x - 2 x^{2}}$ .

Lời giải:

a) Ta có: $y = - x^{2} + 4 x + 3 = - {(x - 2)}^{2} + 7 \leq 7$ với mọi số thực x.

Dấu “=” xảy ra khi $x - 2 = 0 \Leftrightarrow x = 2$ .

Do đó, $max f (x) = f (2) = 7$ , hàm số không có giá trị nhỏ nhất.

b) GTLN, GTNN của $y = x^{3} - 2 x^{2} + 1$ trên $[0; + \infty)$

Ta có: $y^{'} = 3 x^{2} - 4 x, y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 (t m) \\ x = \frac{4}{3} (t m) \end{array}$

Bảng biến thiên:

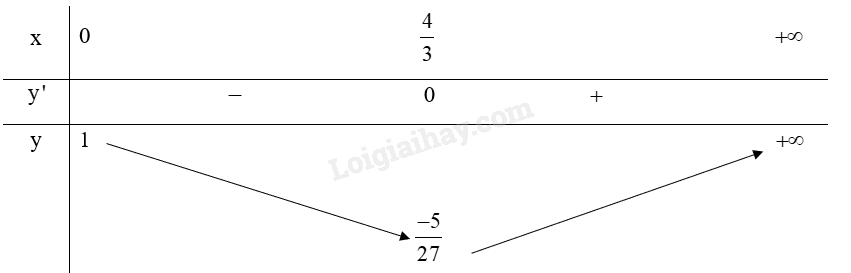
Do đó, $min_{[0; + \infty)} y = y (\frac{4}{3}) = \frac{- 5}{27}$ , hàm số không có giá trị lớn nhất.

c) Ta có: $y^{'} = \frac{(2 x - 2) (x - 1) - (x^{2} - 2 x + 3)}{{(x - 1)}^{2}} = \frac{x^{2} - 2 x - 1}{{(x - 1)}^{2}}$

$y^{'} = 0 \Leftrightarrow x = 1 + \sqrt{2}$ (do $x \in (1; + \infty)$ )

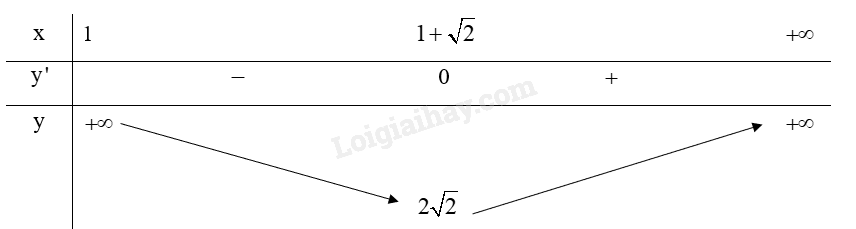
Do đó, $min_{(1; + \infty)} y = y (1 + \sqrt{2}) = 2 \sqrt{2}$ , hàm số không có giá trị lớn nhất trên $(1; + \infty)$ .

d) Tập xác định của hàm số là: $D = [0; 2]$

$y^{'} = \frac{{(4 x - 2 x^{2})}^{'}}{2 \sqrt{4 x - 2 x^{2}}} = \frac{4 - 4 x}{2 \sqrt{4 x - 2 x^{2}}} = \frac{2 (1 - x)}{\sqrt{4 x - 2 x^{2}}}$

$y^{'} = 0 \Leftrightarrow x = 1 (t m)$

$y (0) = 0; y (1) = \sqrt{2}; y (2) = 0$

Do đó, $max_{[0; 2]} y = y (1) = \sqrt{2}, min_{[0; 2]} y = y (0) = y (2) = 0$

Bài 1.11 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = x^{4} - 2 x^{2} + 3$ ;

b) $y = x . e^{- x}$ ;

c) $y = x \ln x$ ;

d) $y = \sqrt{x - 1} + \sqrt{3 - x}$ .

Lời giải:

a) $y = x^{4} - 2 x^{2} + 3$

$y^{'} = 4 x^{3} - 4 x, y^{'} = 0 \Leftrightarrow 4 x^{3} - 4 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = \pm 1 \end{array}$

$y (0) = 3; y (1) = y (- 1) = 2$

Do đó, $max_{(- \infty; + \infty)} y = y (0) = 3, min_{(- \infty; + \infty)} y = y (1) = y (- 1) = 2$

b) Ta có: $y^{'} = e^{- x} - x . e^{- x}, y^{'} = 0 \Leftrightarrow e^{- x} - x . e^{- x} = 0 \Leftrightarrow e^{- x} (1 - x) = 0 \Leftrightarrow x = 1$

Bảng biến thiên:

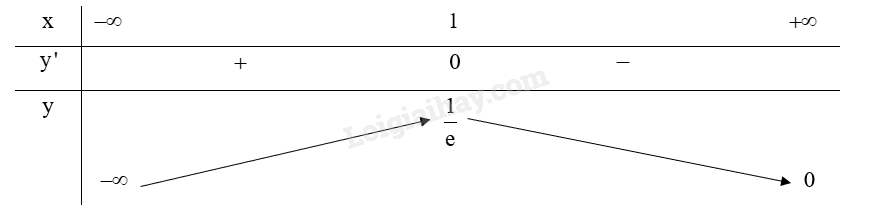
Do đó, $max_{(- \infty; + \infty)} y = y (1) = \frac{1}{e}$ , hàm số không có giá trị nhỏ nhất.

c) Tập xác định của hàm số là: $D = (0; + \infty)$

$y^{'} = \ln x + x . \frac{1}{x} = \ln x + 1, y^{'} = 0 \Leftrightarrow \ln x + 1 = 0 \Leftrightarrow x = \frac{1}{e}$ (thỏa mãn)

Bảng biến thiên:

Hàm số không có giá trị lớn nhất, $min_{(0; + \infty)} y = y (\frac{1}{e}) = \frac{- 1}{e}$

d) Tập xác định của hàm số là $[1; 3]$ .

$y^{'} = \frac{1}{2 \sqrt{x - 1}} - \frac{1}{2 \sqrt{3 - x}}, y^{'} = 0 \Leftrightarrow \frac{1}{2 \sqrt{x - 1}} - \frac{1}{2 \sqrt{3 - x}} = 0 \Leftrightarrow \frac{\sqrt{3 - x} - \sqrt{x - 1}}{2 \sqrt{3 - x} \sqrt{x - 1}} = 0$

$\Leftrightarrow \sqrt{3 - x} = \sqrt{x - 1} \Leftrightarrow 3 - x = x - 1 \Leftrightarrow x = 2 (t m)$

$y (1) = \sqrt{2}; y (2) = 2; y (3) = \sqrt{2}$

Do đó, $max_{[1; 3]} y = y (2) = 2, min_{[1; 3]} y = y (1) = y (3) = \sqrt{2}$

Bài 1.12 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = 2 x^{3} - 6 x + 3$ trên đoạn $[- 1; 2]$ ;

b) $y = x^{4} - 3 x^{2} + 2$ trên đoạn $[0; 3]$ ;

c) $y = x - \sin 2 x$ trên đoạn $[0; π]$ ;

d) $y = (x^{2} - x) e^{x}$ trên đoạn $[0; 1]$ .

Lời giải:

a) Ta có: $y^{'} = 6 x^{2} - 6, y^{'} = 0 \Leftrightarrow 6 x^{2} - 6 = 0 \Leftrightarrow x = \pm 1$ (thỏa mãn)

$y (- 1) = 7, y (1) = - 1, y (2) = 7$

Do đó, $max_{[- 1; 2]} y = y (2) = y (- 1) = 7, min_{[- 1; 2]} y = y (1) = - 1$

b) Ta có: $y^{'} = 4 x^{3} - 6 x, y^{'} = 0 \Leftrightarrow 4 x^{3} - 6 x = 0 \Leftrightarrow x = 0; x = \frac{\sqrt{6}}{2}$ (do $x \in [0; 3]$ )

$y (0) = 2; y (\frac{\sqrt{6}}{2}) = \frac{- 1}{4}; y (3) = 56$

Do đó, $max_{[0; 3]} y = y (3) = 56, min_{[0; 3]} y = y (\frac{\sqrt{6}}{2}) = \frac{- 1}{4}$

c) Ta có: $y^{'} = 1 - 2 \cos 2 x, y^{'} = 0 \Leftrightarrow 1 - 2 \cos 2 x = 0 \Leftrightarrow \cos 2 x = \frac{1}{2} \Leftrightarrow x = \pm \frac{π}{6} + k π (k \in Z)$

Mà $x \in [0; π] \Rightarrow x = \frac{π}{6}; x = \frac{5 π}{6}$

$y (0) = 0; y (\frac{π}{6}) = \frac{π}{6} - \frac{\sqrt{3}}{2}; y (\frac{5 π}{6}) = \frac{5 π}{6} + \frac{\sqrt{3}}{2}; y (π) = π$

Do đó, $max_{[0; π]} y = y (\frac{5 π}{6}) = \frac{5 π}{6} + \frac{\sqrt{3}}{2}, min_{[0; π]} y = y (\frac{π}{6}) = \frac{π}{6} - \frac{\sqrt{3}}{2}$

d) $y^{'} = (2 x - 1) e^{x} + (x^{2} - x) e^{x} = e^{x} (x^{2} + x - 1)$

$y^{'} = 0 \Leftrightarrow e^{x} (x^{2} + x - 1) = 0 \Leftrightarrow x = \frac{- 1 + \sqrt{5}}{2}$ (do $x \in [0; 1]$ )

$y (0) = 0; y (\frac{- 1 + \sqrt{5}}{2}) = (2 - \sqrt{5}) e^{\frac{- 1 + \sqrt{5}}{2}}; y (1) = 0$

Do đó, $max_{[0; 1]} y = y (0) = y (1) = 0, min_{[0; 1]} y = y (\frac{- 1 + \sqrt{5}}{2}) = (2 - \sqrt{5}) e^{\frac{- 1 + \sqrt{5}}{2}}$

Bài 1.13 trang 19 SGK Toán 12 Tập 1: Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Lời giải:

Gọi chiều dài của hình chữ nhật là x (cm, $0 < x < 12$ )

Chiều rộng của hình chữ nhật là $12 - x (c m)$

Diện tích của hình chữ nhật là: $x (12 - x) = - x^{2} + 12 x (c m^{2})$

Đặt $S (x) = - x^{2} + 12 x, x \in (0; 12)$

$S^{'} (x) = - 2 x + 12, S^{'} (x) = 0 \Leftrightarrow x = 6 (t m)$

Bảng biến thiên:

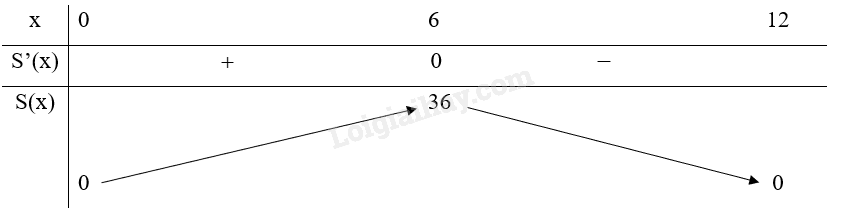
Do đó, trong các hình có cùng chu vi thì hình chữ nhật có diện tích lớn nhất là $36 c m^{2}$ .

Bài 1.14 trang 19 SGK Toán 12 Tập 1: Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng $108 c m^{2}$ như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

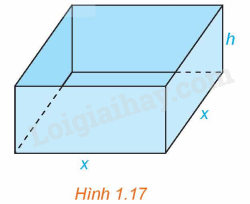
Lời giải:

Hình hộp trên có độ dài cạnh đáy là x (cm, $x > 0$ ) và chiều cao là h (cm, $h > 0$ )

Diện tích bề mặt của hình hộp là $108 c m^{2}$ nên $x^{2} + 4 x h = 108 \Rightarrow h = \frac{108 - x^{2}}{4 x} (c m)$

Thể tích của hình hộp là: $V = x^{2} . h = x^{2} . \frac{108 - x^{2}}{4 x} = \frac{108 x - x^{3}}{4} (c m^{3})$

Ta có: $V^{'} = \frac{- 3 x^{2} + 108}{4}, V^{'} = 0 \Leftrightarrow x = 6$ (do $x > 0$ )

Bảng biến thiên:

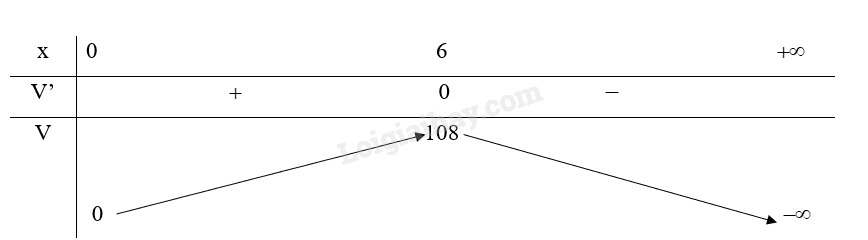
Do đó, thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy $x = 6$ cm

Khi đó, chiều cao của hình hộp là: $\frac{108 - 6^{2}}{4.6} = 3 (c m)$ .

Bài 1.15 trang 19 SGK Toán 12 Tập 1: Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích

1 000 c m^{3}

. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/

c m^{2}

, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/

c m^{2}

. Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.

Lời giải:

Gọi bán kính đáy của bình là x (cm, $x > 0$ )

Chiều cao của bình là: $\frac{1000}{π . x^{2}} (c m)$

Chi phí để sản xuất một chiếc bình là: $T (x) = 2.1, 2. π . x^{2} + 0, 75. \frac{2000}{x} = 2, 4 π . x^{2} + \frac{1500}{x}$ (nghìn đồng)

Để chi phí sản xuất mỗi chiếc bình là thấp nhất thì T(x) là nhỏ nhất.

$T^{'} (x) = 4, 8 π x - \frac{1500}{x^{2}}, T^{'} (x) = 0 \Leftrightarrow x = \sqrt[3]{\frac{625}{2 π}}$ (thỏa mãn)

Bảng biến thiên:

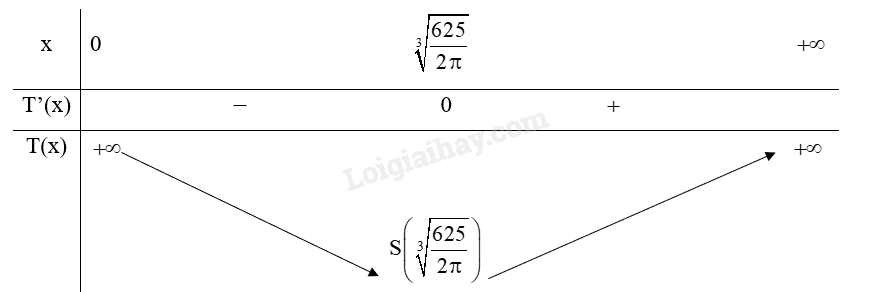
Để chi phí sản xuất mỗi chiếc bình là nhỏ nhất thì bán kính đáy của bình là $\sqrt[3]{\frac{625}{2 π}} c m$ và chiều cao của bình là: $\frac{1000}{π . {(\sqrt[3]{\frac{625}{2 π}})}^{2}} (c m)$