Bài 1.10 trang 19 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Bài 1.10 trang 19 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Mai Hương Ngày: 14-03-2024 Lớp 12

147

Với giải Bài 1.10 trang 19 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Bài 1.10 trang 19 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Bài 1.10 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) $y = - x^{2} + 4 x + 3$ ;
b) $y = x^{3} - 2 x^{2} + 1$ trên $[0; + \infty)$ ;
c) $y = \frac{x^{2} - 2 x + 3}{x - 1}$ trên $(1; + \infty)$ ;
d) $y = \sqrt{4 x - 2 x^{2}}$ .

Lời giải:

a) Ta có: $y = - x^{2} + 4 x + 3 = - {(x - 2)}^{2} + 7 \leq 7$ với mọi số thực x.

Dấu “=” xảy ra khi $x - 2 = 0 \Leftrightarrow x = 2$ .

Do đó, $max f (x) = f (2) = 7$ , hàm số không có giá trị nhỏ nhất.

b) GTLN, GTNN của $y = x^{3} - 2 x^{2} + 1$ trên $[0; + \infty)$

Ta có: $y^{'} = 3 x^{2} - 4 x, y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 0 (t m) \\ x = \frac{4}{3} (t m) \end{array}$

Bảng biến thiên:

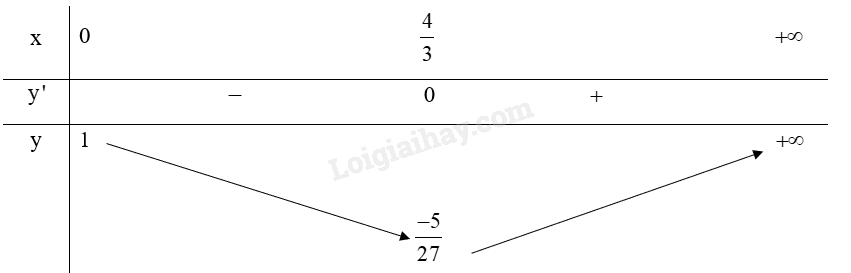
Do đó, $min_{[0; + \infty)} y = y (\frac{4}{3}) = \frac{- 5}{27}$ , hàm số không có giá trị lớn nhất.

c) Ta có: $y^{'} = \frac{(2 x - 2) (x - 1) - (x^{2} - 2 x + 3)}{{(x - 1)}^{2}} = \frac{x^{2} - 2 x - 1}{{(x - 1)}^{2}}$

$y^{'} = 0 \Leftrightarrow x = 1 + \sqrt{2}$ (do $x \in (1; + \infty)$ )

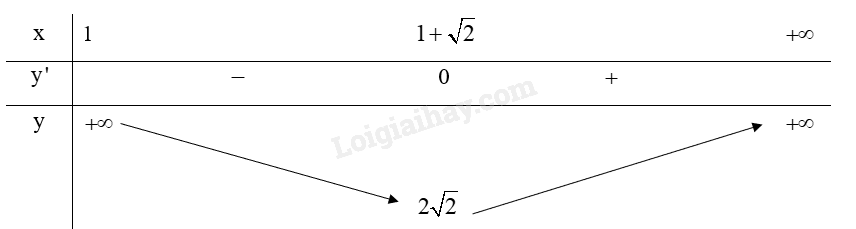
Do đó, $min_{(1; + \infty)} y = y (1 + \sqrt{2}) = 2 \sqrt{2}$ , hàm số không có giá trị lớn nhất trên $(1; + \infty)$ .

d) Tập xác định của hàm số là: $D = [0; 2]$

$y^{'} = \frac{{(4 x - 2 x^{2})}^{'}}{2 \sqrt{4 x - 2 x^{2}}} = \frac{4 - 4 x}{2 \sqrt{4 x - 2 x^{2}}} = \frac{2 (1 - x)}{\sqrt{4 x - 2 x^{2}}}$

$y^{'} = 0 \Leftrightarrow x = 1 (t m)$

$y (0) = 0; y (1) = \sqrt{2}; y (2) = 0$

Do đó, $max_{[0; 2]} y = y (1) = \sqrt{2}, min_{[0; 2]} y = y (0) = y (2) = 0$

Hoạt động 1 trang 15 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = x^{2} - 2 x$ với $x \in [0; 3]$ , có đồ thị như Hình 1.15.

Luyện tập 1 trang 17 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

Hoạt động 2 trang 17 SGK Toán 12 Tập 1: Xét hàm số $y = f (x) = x^{3} - 2 x^{2} + 1$ trên đoạn $[- 1; 2]$ , với đồ thị như Hình 1.16.

Luyện tập 2 trang 18 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

Vận dụng trang 18 SGK Toán 12 Tập 1: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số $N (t) = - t^{3} + 12 t^{2}, 0 \leq t \leq 12,$

Bài 1.10 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) $y = - x^{2} + 4 x + 3$ ;

Bài 1.11 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a)

y = x^{4} - 2 x^{2} + 3

;

Bài 1.12 trang 19 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a)

y = 2 x^{3} - 6 x + 3

[- 1; 2]

;

Bài 1.13 trang 19 SGK Toán 12 Tập 1: Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Bài 1.14 trang 19 SGK Toán 12 Tập 1: Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng $108 c m^{2}$ như Hình 1.17.

Bài 1.15 trang 19 SGK Toán 12 Tập 1: Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích

1 000 c m^{3}

. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/

c m^{2}

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 12

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

135

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

195

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

200

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

140

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.