Hoạt động 3 trang 23 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Hoạt động 3 trang 23 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Mai Hương Ngày: 14-03-2024 Lớp 12

87

Với giải Hoạt động 1 trang 20 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 3: Đường tiệm cận của đồ thị hàm số giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Hoạt động 3 trang 23 Toán 12 Tập 1 | Kết nối tri thức Giải Toán lớp 12

Hoạt động 3 trang 23 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = x - 1 + \frac{2}{x + 1}$ có đồ thị (C) và đường thẳng $y = x - 1$ như Hình 1.24.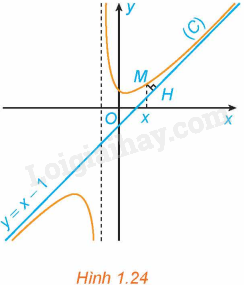

a) Với $x > - 1$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = x - 1$ . Có nhận xét gì về khoảng cách MH khi $x \to + \infty$ ?

b) Chứng tỏ rằng $lim_{x \to + \infty} [f (x) - (x - 1)] = 0$ . Tính chất này thể hiện trên Hình 1.24 như thế nào?

Lời giải:

a) Nhìn vào đồ thị ta thấy, khi $x \to + \infty$ thì khoảng cách MH tiến tới 0.

b) Ta có: $lim_{x \to + \infty} [f (x) - (x - 1)] = lim_{x \to + \infty} [x - 1 + \frac{2}{x + 1} - (x - 1)] = lim_{x \to + \infty} \frac{2}{x + 1} = lim_{x \to + \infty} \frac{\frac{2}{x}}{1 + \frac{1}{x}} = 0$

Tính chất này được thể hiện trong Hình 1.24 là: Khoảng cách từ điểm M của đồ thị hàm số (C) đến đường thẳng $y = x - 1$ tiến đến 0 khi $x \to + \infty$ .

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Hoạt động 1 trang 20 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = \frac{2 x + 1}{x}$ có đồ thị (C). Với $x > 0$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $y = 2$ (H.1.19)

Luyện tập 1 trang 21 SGK Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y = f (x) = \frac{2 x - 1}{x - 1}$ .

Vận dụng 1 trang 21 SGK Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu.

Hoạt động 2 trang 21 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = \frac{x}{x - 1}$ có đồ thị (C). Với $x > 1$ , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng $x = 1$ (H.1.22)

Luyện tập 2 trang 22 SGK Toán 12 Tập 1: Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = f (x) = \frac{2 x + 1}{x - 4}$ .

Vận dụng 2 trang 22 SGK Toán 12 Tập 1: Để loại bỏ p% một loài tảo độc khỏi hồ nước, người ta ước tính chi phí bỏ ra là $C (p) = \frac{45 p}{100 - p}$ (triệu đồng), với $0 \leq p < 100$ .

Hoạt động 3 trang 23 SGK Toán 12 Tập 1: Cho hàm số $y = f (x) = x - 1 + \frac{2}{x + 1}$ có đồ thị (C) và đường thẳng $y = x - 1$ như Hình 1.24.

Luyện tập 3 trang 24 SGK Toán 12 Tập 1: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y = f (x) = \frac{x^{2} - 4 x + 2}{1 - x}$ .

Bài 1.16 trang 25 SGK Toán 12 Tập 1: Hình 1.26 là đồ thị của hàm số $y = f (x) = \frac{2 x^{2}}{x^{2} - 1}$

Bài 1.17 trang 25 SGK Toán 12 Tập 1: Đường thẳng $x = 1$ có phải là tiệm cận đứng của đồ thị hàm số $y = \frac{x^{2} + 2 x - 3}{x - 1}$ không?

Bài 1.18 trang 25 SGK Toán 12 Tập 1: Tìm các tiệm cận của đồ thị hàm số sau:

Bài 1.19 trang 25 SGK Toán 12 Tập 1: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là $C (x) = 2 x + 50$ (triệu đồng).

Bài 1.20 trang 25 SGK Toán 12 Tập 1: Một mảnh vườn hình chữ nhật có diện tích bằng $144 m^{2}$ . Biết độ dài một cạnh của mảnh vườn là x (m).

Xem thêm các bài giải SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Từ khóa :

Giải bài tập Toán 12

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

205

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

243

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

263

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

219

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.