Toán 12 (Chân trời sáng tạo) Bài 1: Tính đơn điệu và cực trị của hàm số

Mai Hương Ngày: 15-03-2024 Lớp 12

230

Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Chân trời sáng tạo) Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 1 từ đó học tốt môn Toán 12.

Toán 12 (Chân trời sáng tạo) Bài 1: Tính đơn điệu và cực trị của hàm số

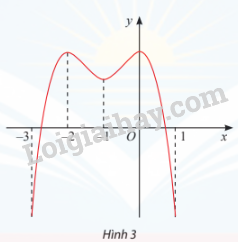
Thực hành 1 trang 7 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3.

Lời giải:

Hàm số đồng biến trên các khoảng (−3; -2) và (-1; 0)

Hàm số nghịch biến trên khoảng (-2; -1) và (0; 1)

Khám phá 1 trang 7 SGK Toán 12 Tập 1: Cho hàm số y = f(x) = $x^{2}$

a) Từ đồ thị của hàm số y = f(x) (Hình 4), hãy chỉ ra các

khoảng đồng biến và nghịch biến của hàm số đã cho.

b) Tính đạo hàm f '(x) và xét dấu f '(x).

c) Từ đó, nhận xét về mối liên hệ giữa các khoảng đồng biến,

nghịch biến của hàm số với dấu của f '(x).

Lời giải:

a) Hàm số đồng biến trên khoảng (0; $+ \infty$ )

Hàm số nghịch biến trên khoảng ( $- \infty$ ; 0)

b) f '(x) = ( $x^{2}$ )' = 2x

Ta có:

f '(x) > 0 $\Leftrightarrow 2 x > 0 \Leftrightarrow x > 0$

f '(x) < 0 $\Leftrightarrow 2 x < 0 \Leftrightarrow x < 0$

c) Nhận xét:

f’(x) > 0 trên K thì y = f(x) đồng biến trên K

f’(x) < 0 trên K thì y = f(x) nghịch biến trên K

Thực hành 2 trang 9 SGK Toán 12 Tập 1: Xét tính đơn điệu của các hàm số sau:

a) $f (x) = x^{3} - 6 x^{2} + 9 x$

b) $g (x) = \frac{1}{x}$

Lời giải:

a) $f (x) = x^{3} - 6 x^{2} + 9 x$

Tập xác định: $D = R$

$f^{'} (x) = 3 x^{2} - 12 x + 9$

$f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = 1 \end{array}$

Bảng biến thiên:

Vậy hàm số $f (x) = x^{3} - 6 x^{2} + 9 x$ đồng biến trên các khoảng ( $- \infty$ ; 1) và (0; $+ \infty$ ), nghịch biến trên khoảng (1; 3)

b) $g (x) = \frac{1}{x}$

Tập xác định: $D = R ∖ {0}$

$g^{'} (x) = - \frac{1}{x^{2}}$

Vì $x^{2} > 0 \forall x \in R ∖ {0}$ nên $g^{'} (x) < 0 \forall x \in R ∖ {0}$

Bảng biến thiên:

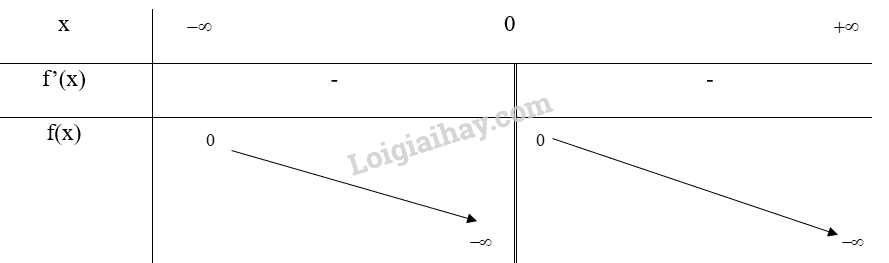
Vậy hàm số $g (x) = \frac{1}{x}$ nghịch biến trên các khoảng ( $- \infty$ ; 0) và (0; $+ \infty$ )

Thực hành 3 trang 9 SGK Toán 12 Tập 1: Chứng minh rằng hàm số $f (x) = 3 x - s i n x$ đồng biến trên $R$

Lời giải:

Tập xác định: $D = R$

$f^{'} (x) = 3 - \cos x$

Ta có: $- 1 \leq \cos x \leq 1$ nên $2 \leq 3 - \cos x \leq 4$ . Vì vậy $f^{'} (x) > 0 \forall x \in R$

=> Hàm số $f (x) = 3 x - s i n x$ đồng biến trên $R$

Vận dụng 1 trang 9 SGK Toán 12 Tập 1: Hãy trả lời câu hỏi trong Khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số $h (t) = 6 t^{3} - 81 t^{2} + 324 t$ với $0 \leq t \leq 8$

Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức $h (t) = 6 t^{3} - 81 t^{2} + 324 t$ . Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?

Lời giải:

$h (t) = 6 t^{3} - 81 t^{2} + 324 t$

Tập xác định: $D = R$

$h^{'} (t) = 18 t^{2} - 162 t + 324$

$h^{'} (t) = 0 \Leftrightarrow [\begin{array}{l} t = 3 \\ t = 6 \end{array}$

Bảng biến thiên:

Trong thời gian từ lúc xuất phát đến thời điểm 3 phút, độ cao của khinh khí cầu tăng dần từ 0m lên 405m

Độ cao của khinh khí cầu tăng dần từ 0m lên 405m trong thời gian từ lúc xuất phát đến thời điểm 3 phút, từ 324m lên 480m trong thời gian từ 6 phút đến 8 phút

Độ cao của khinh khí cầu giảm dần từ 405m xuống 324m trong thời gian từ 3 phút đến 6 phút

Khám phá 2 trang 10 SGK Toán 12 Tập 1: Quan sát đồ thị của hàm số $y = f (x) = x^{3} - - 3 x^{2} + 1$ trong Hình 5.

a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi $x \neq 0$ .

b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi $x \neq 2$ .

c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi $x \neq 1$ hoặc f(x) < f(1) với mọi $x \neq 1$ ?

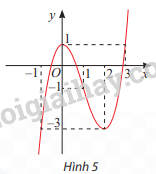
Lời giải:

a) Trên khoảng (-1; 2), f(x) < f(0) với mọi $x \neq 0$

b) Trên khoảng (0; 3), f(x) > f(2) với mọi $x \neq 2$

c) Không tồn tại khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi $x \neq 1$ hoặc f(x) < f(1) với mọi $x \neq 1$

Thực hành 4 trang 11 SGK Toán 12 Tập 1: Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8

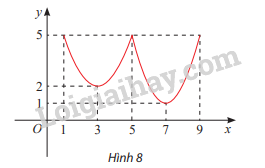
Lời giải:

Hàm số y = f (x) có:

x = 5 là điểm cực đại vì f (x) < f(5) với mọi $x \in (3; 7) ∖ {5}$ , $y_{c d} = f (5) = 5$

x = 3 là điểm cực tiểu vì f(x) > f(3) với mọi $x \in (1; 5) ∖ {3}$ , $y_{c t} = f (3) = 2$

x=7 là điểm cực tiểu vì f(x) > f(7) với mọi $x \in (5; 9) ∖ {7}$ , $y_{c t} = f (7) = 1$

Khám phá 3 trang 11 SGK Toán 12 Tập 1: Đồ thị của hàm số $y = {\begin{cases} x^{2} k h i x \leq 1 \\ 2 - x k h i x > 1 \end{cases}$ được cho ở Hình 9.

a) Tìm điểm cực đại và điểm cực tiểu của hàm số.

b) Tại x = 1, hàm số có đạo hàm không?

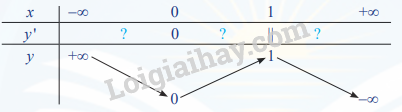
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại và điểm cực tiểu.

Lời giải:

a) Hàm số y = f (x) có:

x = 1 là điểm cực đại vì f (x) < f(1) với mọi $x \in (0; + \infty) ∖ {0}$

x = 0 là điểm cực tiểu vì f(x) > f(0) với mọi $x \in (+ \infty; 1) ∖ {0}$

b) Tại x = 1, hàm số không có đạo hàm vì đồ thị bị gấp khúc

Nhận xét: Khi đi qua các điểm cực đại và cực tiểu thì y’ đổi dấu

Thực hành 5 trang 12 SGK Toán 12 Tập 1: Tìm cực trị của hàm số $g (x) = \frac{x^{2} + x + 4}{x + 1}$

Lời giải:

Tập xác định: $D = R ∖ {- 1}$

$g^{'} (x) = \frac{x^{2} + 2 x - 3}{x^{2} + 2 x + 1} = 0 \Leftrightarrow [\begin{array}{l} x = 1 \\ x = - 3 \end{array}$

Bảng biến thiên:

Vậy hàm số đạt cực tiểu tại x = -3, $y_{c t} = f (- 3) = - 5$ , đạt cực đại tại x = 1, $y_{c d} = f (1) = 3$

Vận dụng 2 trang 12 SGK Toán 12 Tập 1: Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số $y = h (x) = - \frac{1}{1320000} x^{3} + \frac{9}{3520} x^{2} - \frac{81}{44} x + 840$ với $0 \leq x \leq 2000$

Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000]

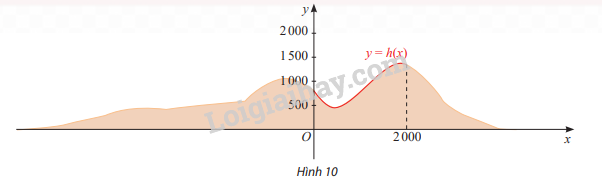
Lời giải:

Tập xác định: $D = [0; 2000]$

$h^{'} (x) = - \frac{1}{440000} x^{2} + \frac{9}{1760} x - \frac{81}{44} = 0 \Leftrightarrow [\begin{array}{l} x = 1800 \\ x = 450 \end{array}$

Bảng biến thiên:

Vậy trên đoạn [0; 2000]:

Tọa độ đỉnh cực tiểu của dãy núi là (450; 460,3125)

Tọa độ đỉnh cực đại của dãy núi là (1800; 1392,27)

Bài 1 trang 13 SGK Toán 12 Tập 1: Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.

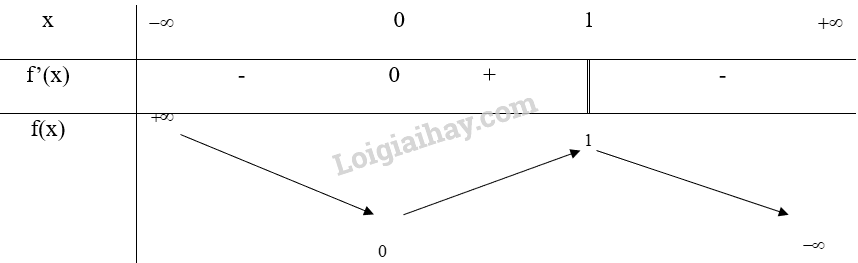
Lời giải:

a) Hàm số đồng biến trên khoảng (-1;2) và (4;5), nghịch biến trên khoảng (-1;0) và (2;4)

Hàm số đạt cực đại tại x = 2, $y_{c d} = f (2) = 2$ , đạt cực tiểu tại x = 0, $y_{c t} = f (0) = - 1$ và x = 4, $y_{c t} = f (4) = - 1$

b) Hàm số đồng biến trên khoảng (-3;-1) và (1;3), nghịch biến trên khoảng (-1;1)

Hàm số đạt cực đại tại x = -1, $y_{c d} = f (- 1) = 3$ , đạt cực tiểu tại x = 1, $y_{c t} = f (1) = - 1$

Bài 3 trang 13 SGK Toán 12 Tập 1: Tìm cực trị của các hàm số sau:

a) $y = 2 x^{3} + 3 x^{2} - - 36 x + 1$
b) $y = \frac{x^{2} - 8 x + 10}{x - 2}$
c) $y = \sqrt{- x^{2} + 4}$

Lời giải:

a) $y = 2 x^{3} + 3 x^{2} - - 36 x + 1$

Tập xác định: $D = R$

$y^{'} = 6 x^{2} + 6 x - 36$

$y^{'} = 0 \Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 3 \end{array}$

Bảng biến thiên:

Hàm số đạt cực đại tại x = -3, $y_{c d} = f (- 3) = 82$ , đạt cực tiểu tại x = 2, $y_{c t} = f (2) = - 43$

b) $y = \frac{x^{2} - 8 x + 10}{x - 2}$

Tập xác định: $D = R ∖ {2}$

$y^{'} = \frac{x^{2} - 4 x + 6}{{(x - 2)}^{2}}$

Ta có: ${\begin{cases} (x^{2} - 4 x + 6) > 0 \forall x \in R ∖ {2} \\ (x - 2)^{2} > 0 \forall x \in R ∖ {2} \end{cases}$ nên $y^{'} > 0 \forall x \in R ∖ {2}$

Bảng biến thiên:

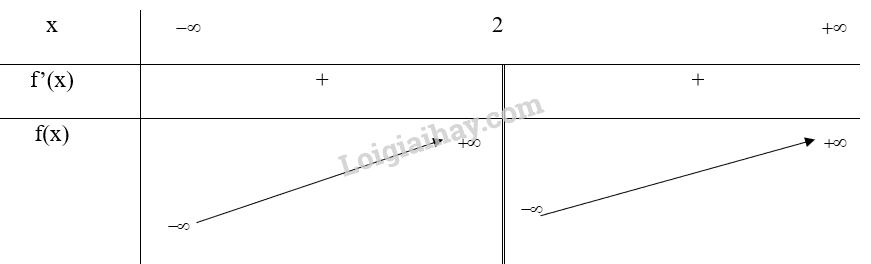
Vậy hàm số không có điểm cực trị

c) $y = \sqrt{- x^{2} + 4}$

Tập xác định: $D = (- 2; 2)$

$y^{'} = \frac{- x}{\sqrt{- x^{2} + 4}}$

$y^{'} = 0 \Leftrightarrow x = 0$

Bảng biến thiên:

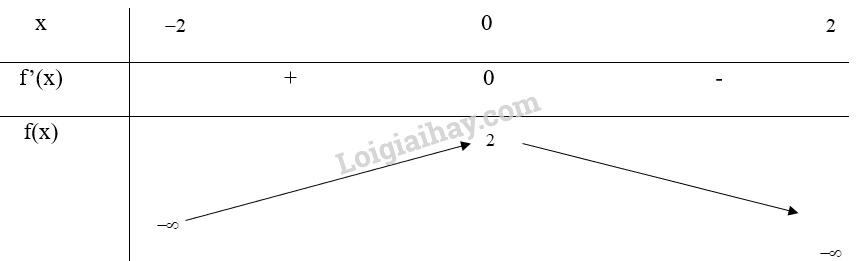
Hàm số đạt cực đại tại x = 0, $y_{c d} = f (0) = 2$

Bài 4 trang 13 SGK Toán 12 Tập 1: Chứng minh rằng hàm số $y = \frac{2 x + 1}{x - 3}$ nghịch biến trên từng khoảng xác định của nó

Lời giải:

Tập xác định: $D = R ∖ {3}$

$y^{'} = \frac{- 7}{{(x - 3)}^{2}}$

Ta có: $(x - 3)^{2} > 0 \forall x \in R ∖ {3}$ nên $y^{'} < 0 \forall x \in R ∖ {3}$

Vậy hàm số $y = \frac{2 x + 1}{x - 3}$ nghịch biến trên $R ∖ {3}$

Bài 5 trang 13 SGK Toán 12 Tập 1: Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức $f (x) = 0, 01 x^{3} - - 0, 04 x^{2} + 0, 25 x + 0, 44$ (tỉ USD) với x là số năm tính từ 2010 đến 2017 ( $0 \leq x \leq 7$ ).
a) Tính đạo hàm của hàm số y = f(x).
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

Lời giải:

a) $y^{'} = f^{'} (x) = 0, 03 x^{2} - 0, 08 x + 0, 25$

b) Tập xác định: $D = [0; 7]$

Ta có: $y^{'} = f^{'} (x) > 0 \forall x \in R$ nên $y = f (x)$ luôn đồng biến $\forall x \in [0; 7]$

Vậy kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

Bài 6 trang 13 SGK Toán 12 Tập 1: Xét một chất điểm chuyển động dọc theo trục

O x

. Toạ độ của chất điểm tại thời điểm

t

được xác định bởi hàm số

x (t) = t^{3} - 6 t^{2} + 9 t

với

t \geq 0

. Khi đó

x^{'} (t)

là vận tốc của chất điểm tại thời điểm

t

, kí hiệu

v (t)

;

v^{'} (t)

là gia tốc chuyển động của chất điểm tại thời điểm

t

, kí hiệu

a (t)

a) Tìm các hàm $v (t)$ và $a (t)$
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Lời giải:

a) $v (t) = x^{'} (t) = 3 t^{2} - 12 t + 9$

$a (t) = v^{'} (t) = 6 t - 12$

b) Tập xác định: $D = [0; + \infty]$

$a (t) = 0 \Leftrightarrow t = 2$

Bảng biến thiên:

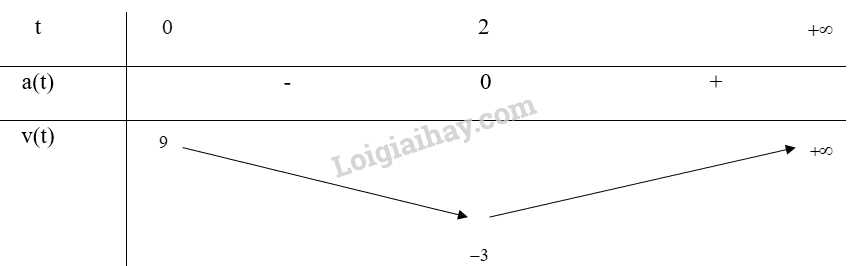
Vậy trong khoảng từ t = 0 đến t = 2 thì vận tốc của chất điểm giảm, từ t = 2 trở đi thì vận tốc của chất điểm tăng

Bài 7 trang 13 SGK Toán 12 Tập 1: Đạo hàm f '(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).

Lời giải:

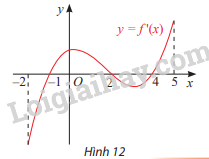
f’(x) > 0 trên các khoảng (-1;2) và (4;5) nên f’(x) đồng biến trên các khoảng (-1;2) và (4;5)

f’(x) < 0 trên các khoảng (-2;-1) và (2;4) nên f’(x) nghịch biến trên các khoảng (-2;-1) và (2;4)

Ta có:

$f^{'} (x) = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 2 \\ x = 4 \end{array}$

Vậy f(x) đạt cực tiểu tại x = -1 và x = 4 do f’(x) đổi dấu từ âm sang dương khi đi qua x = -1 và x = 4, đạt cực đại tại x = 2 do f’(x) đổi dấu từ dương sang âm khi đi qua x = 2

Xem thêm các bài giải SGK Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: