Toptailieu biên soạn và giới thiệu lời giải Toán 12 (Chân trời sáng tạo) Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi SGK Toán 12 Bài 2 từ đó học tốt môn Toán 12.
Toán 12 (Chân trời sáng tạo) Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
a) Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là .
ii) Nhiệt độ cao nhất trong ngày là .
iii) Nhiệt độ cao nhất trong ngày là .
b) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
c) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
Lời giải:
a) Khẳng định đúng là iii) vì nhìn hình ta thấy điểm cao nhất của đồ thị là
b) Thời điểm có nhiệt độ cao nhất trong ngày () là lúc 16 giờ
c) Nhiệt độ thấp nhất trong ngày là
Thực hành 1 trang 16 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
Lời giải:
a) Xét trên đoạn [0;3]
Bảng biến thiên:
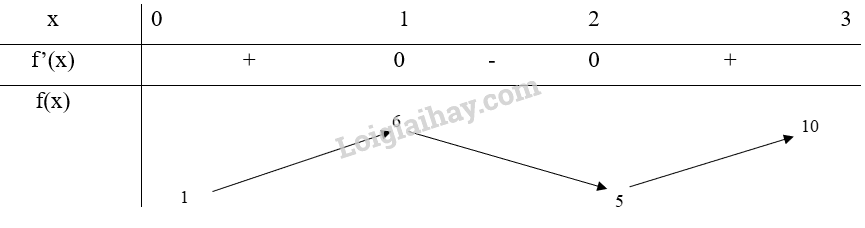
Từ bảng biến thiên, ta thấy và
b) Xét trên khoảng (0;5)
Bảng biến thiên:
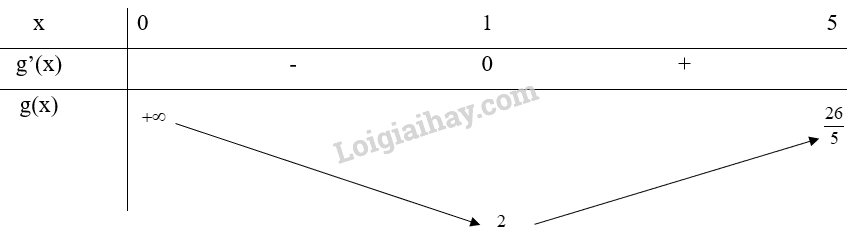
Từ bảng biến thiên, ta thấy và hàm số không tồn tại giá trị lớn nhất trên khoảng (0;5)
c) Xét
Tập xác định:
Tập xác định mới:
Bảng biến thiên:

Từ bảng biến thiên, ta thấy và
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
Lời giải:
Xét trên nửa đoạn
Bảng biến thiên:
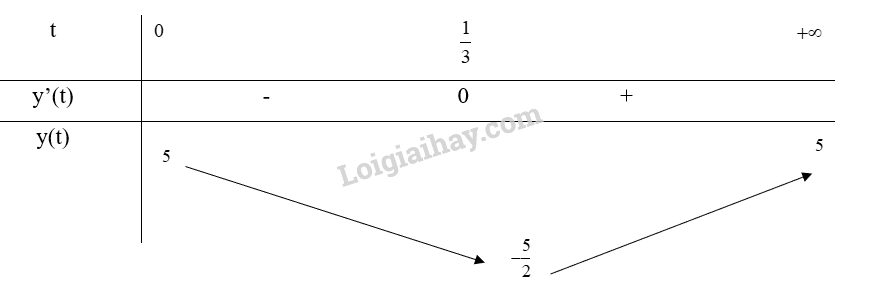
Từ bảng biến thiên, ta thấy và
Vậy vào các thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất và t = giờ thì nồng độ oxygen trong nước thấp nhất
Khám phá 2 trang 16 SGK Toán 12 Tập 1: Hình 3 cho ta đồ thị của ba hàm số
a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?
b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?

Lời giải:
a) đạt giá trị cực đại tại x = 0 và
b) và
Lời giải:
Xét trên đoạn [1;4]
Bảng biến thiên:

Từ bảng biến thiên, ta thấy và
Lời giải:
Đặt một cạnh góc vuông là x (x > 0) thì cạnh còn lại là
Diện tích tam giác vuông là:
Tập xác định:
Tập xác định mới:
Bảng biến thiên:

Từ bảng biến thiên, ta thấy
Vậy diện tích lớn nhất của tam giác là
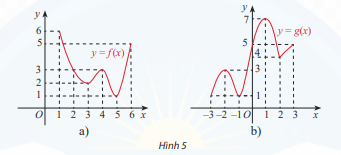
Lời giải:
a) Từ đồ thị, ta thấy và
b) Từ đồ thị, ta thấy và
a) trên đoạn [-1;3]
b) trên đoạn [3;11]
c) trên đoạn [3;7]
d) trên đoạn
Lời giải:
a) Xét trên đoạn [-1;3]
Bảng biến thiên:
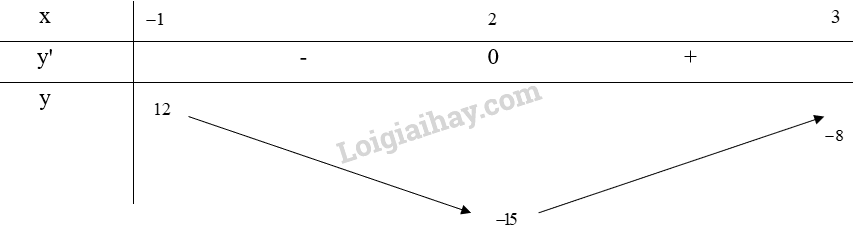
Từ bảng biến thiên, ta thấy và
b) Xét trên đoạn [3;11]
Bảng biến thiên:

Từ bảng biến thiên, ta thấy và
c) Xét trên đoạn [3;7]
Bảng biến thiên:
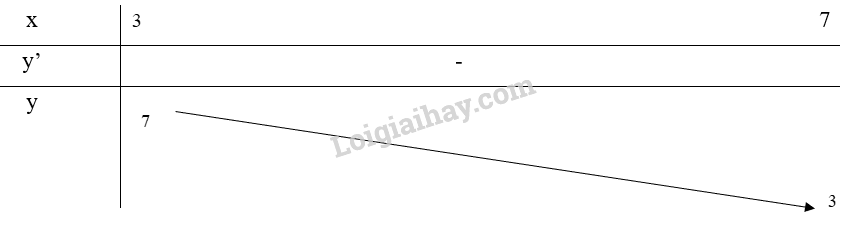
Từ bảng biến thiên, ta thấy và
d) Xét trên đoạn
Ta có:
Bảng biến thiên:
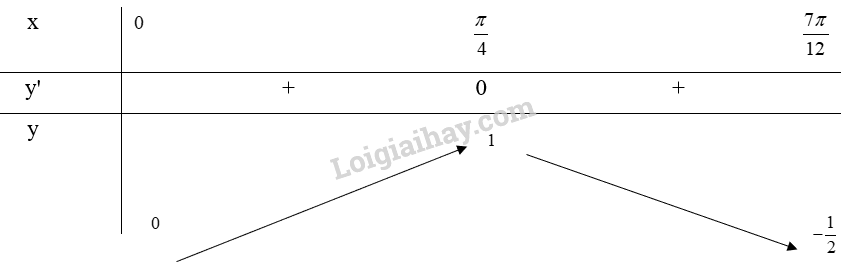
Từ bảng biến thiên, ta thấy và
Bài 3 trang 18 SGK Toán 12 Tập 1: Tìm giá trị nhỏ nhất của các hàm số sau:
a) trên nửa khoảng [-3;2)
b) trên khoảng
Lời giải:
a) Xét trên nửa khoảng [-3;2)
Bảng biến thiên:

Từ bảng biến thiên, ta thấy
b) Xét trên khoảng
Tập xác định:
Bảng biến thiên:

Từ bảng biến thiên, ta thấy hàm số không tồn tại giá trị nhỏ nhất trên khoảng

Lời giải:
Gọi a, b lần lượt là chiều dài và chiều rộng của cửa sổ (m; a,b > 0)
Chu vi cửa sổ là:
Diện tích cửa sổ là:
Bảng biến thiên:
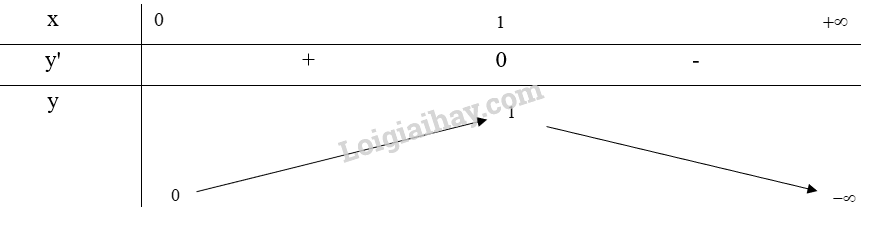
Từ bảng biến thiên, ta thấy
Vậy để diện tích cửa sổ lớn nhất bằng
Bài 5 trang 18 SGK Toán 12 Tập 1: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Lời giải:
Tập xác định:
Tập xác định mới:
Bảng biến thiên:
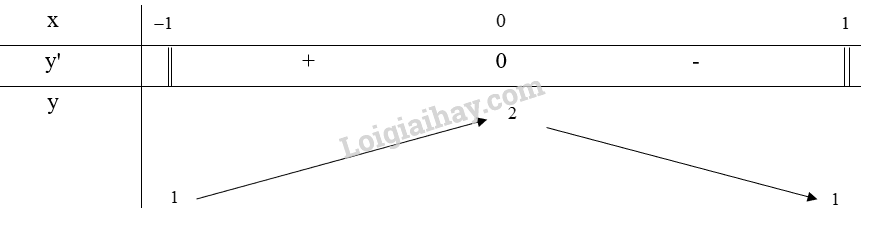
Từ bảng biến thiên, ta thấy và
a) Viết công thức biểu diễn theo .
Lời giải:
a) Ta có:
Thay vào ta được:
b) Đặt
Tập xác định:
Bảng biến thiên:

Từ bảng biến thiên, ta thấy
Vậy nếu giá bán mỗi kilôgam sản phẩm là 7,5 nghìn đồng/kg thì sẽ đạt được doanh thu cao nhất là 112,5 nghìn đồng
Lời giải:
Gọi chiều cao của hộp là h (cm)
Thể tích của hộp là:
Diện tích toàn phần của hộp là:
Tập xác định:
Bảng biến thiên:
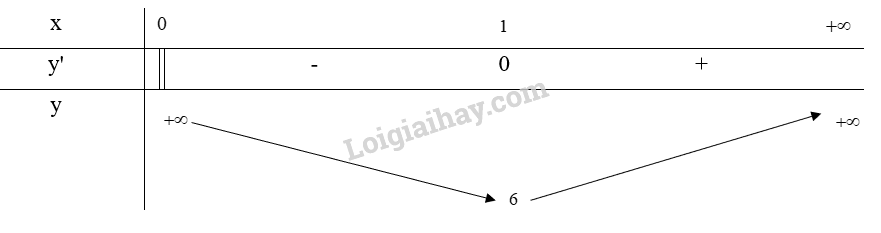
Từ bảng biến thiên, ta thấy
Vậy x = 1cm thì diện tích toàn phần của hộp nhỏ nhất và bằng 6
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.