Lấy một điểm M tùy ý. Chứng minh rằng

Phương Thảo Ngày: 28-10-2022 Lớp 10

403

Với Giải SBT Toán 10 Tập 1 trong Bài 3: Tích của một số với một vecto Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

Lấy một điểm M tùy ý. Chứng minh rằng

Bài 3 trang 97 SBT Toán 10: Lấy một điểm M tùy ý. Chứng minh rằng:

a) I là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{M A} + \vec{M B} = 2 \vec{M I}$

b) G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{M A} + \vec{M B} + \vec{M C} = 3 \vec{M G}$

Lời giải:

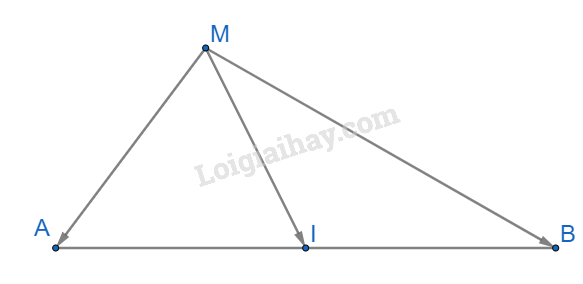
Áp dụng quy tắc ba điểm ta có:

$\vec{M A} + \vec{M B} = (\vec{M I} + \vec{I A}) + (\vec{M I} + \vec{I B}) = 2 \vec{M I} + (\vec{I A} + \vec{I B}) = 2 \vec{M I}$ (đpcm)

(I là trung điểm của AB nên $\vec{I A} + \vec{I B} = \vec{0}$

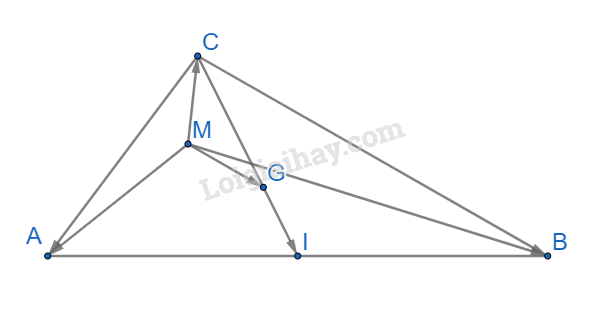
Áp dụng quy tắc ba điểm ta có:

$\begin{array}{l} \vec{M A} + \vec{M B} + \vec{M C} = (\vec{M G} + \vec{G A}) + (\vec{M G} + \vec{G B}) + (\vec{M G} + \vec{G C}) \\ = 3 \vec{M G} + (\vec{G A} + \vec{G B} + \vec{G C}) = 3 \vec{M G} \end{array}$ (đpcm)