Cho nửa đường tròn tâm O có đường kính

Phương Thảo Ngày: 28-10-2022 Lớp 10

176

Với Giải SBT Toán 10 Tập 1 trong Bài 4: Tích vô hướng của hai vecto Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

Cho nửa đường tròn tâm O có đường kính

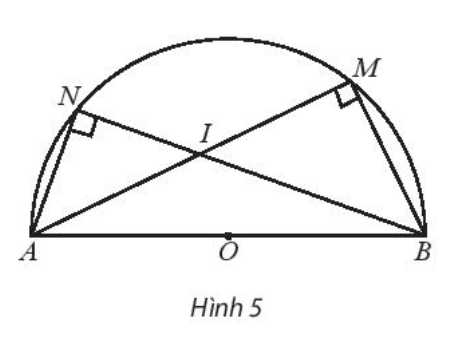
Bài 3 trang 101 SBT Toán 10: Cho nửa đường tròn tâm O có đường kính $A B = 2 R$ . Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như hình 5.

a) Chứng minh: $\vec{A I} . \vec{A M} = \vec{A I} . \vec{A B}; \vec{B I} . \vec{B N} = \vec{A B} . \vec{B A}$

b) Tính $\vec{A I} . \vec{A M} + \vec{B I} . \vec{B N}$ theo R

Lời giải:

a) Ta có:

$\begin{array}{l} \vec{A I} . \vec{A M} = | \vec{A I} | . | \vec{A M} | . \cos (\vec{A I}, \vec{A M}) \\ = A I . A M . \cos 0^{\circ} = A I . A M \end{array}$ (*)

Mặt khác $A M = A B . \cos \hat{M A B}$ , thay vào (*) ta có:

$\begin{array}{l} \vec{A I} . \vec{A M} = A I . A M = A I . A B . \cos \hat{M A B} \\ = | \vec{A I} | . | \vec{A B} | . \cos (\vec{A I}, \vec{A B}) = \vec{A I} . \vec{A B} \end{array}$ (đpcm)

$\begin{array}{l} \vec{B I} . \vec{B N} = | \vec{B I} | . | \vec{B N} | . \cos (\vec{B I}, \vec{B N}) \\ = B I . B N . \cos 0^{\circ} = B I . B N \end{array}$ (**)

Mặt khác $B N = B A . \cos \hat{N B A}$ , thay vào (**) ta có:

$\begin{array}{l} \vec{B I} . \vec{B N} = B I . B N = B I . B A . \cos \hat{N B A} \\ = | \vec{B I} | . | \vec{B A} | . \cos (\vec{B I}, \vec{B A}) = \vec{B I} . \vec{B A} \end{array}$ (đpcm)

b) Từ kết quả của câu a) ta có:

$\begin{array}{l} \vec{A I} . \vec{A M} + \vec{B I} . \vec{B N} = \vec{A I} . \vec{A B} + \vec{B I} . \vec{B A} = \vec{A I} . \vec{A B} + \vec{B I} . (- \vec{A B}) \\ = \vec{A I} . \vec{A B} - \vec{A B} . \vec{B I} = \vec{A B} (\vec{A I} - \vec{B I}) = \vec{A B} (\vec{A I} + \vec{I B}) = {\vec{A B}}^{2} \\ = A B^{2} = {(2 R)}^{2} = 4 R^{2} \end{array}$