Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số trang 51,52,53 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 1: Nhắc lại và bổ sung các khái niệm về hàm số

Phần câu hỏi bài 1 trang 51, 52 Vở bài tập toán 9 tập 1

a) Tính giá trị tương ứng của y theo các giá trị của x rồi điền vào bảng sau: 

b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?  

Phương pháp giải:

a) Thay giá trị của $x$ bằng giá trị của $x_0$ vào hàm số đã cho rồi tính giá trị và điền vào ô tương ứng.

b) Vận dụng kiến thức : Nếu giá trị của biến x tăng lên mà giá trị tương ứng f(x) cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên R.

Ngược lại thì hàm số nghịch biến trên R.

Trả lời:

a) 

b) Khi $x$ lần lượt nhận các giá trị tăng lên thì giá trị tương ứng của các hàm số lại giảm đi.

Vậy hàm số đã cho nghịch biến trên R

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.

b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?

Phương pháp giải:

a) - Với hai giá trị bất kì của $x$ tìm giá trị tương ứng của hàm số.

    - Biểu diễn trên mặt phẳng tọa độ các cặp giá trị vừa tìm được $\left(x;f\left(x\right)\right)$.

b) Vận dụng kiến thức : Nếu giá trị của biến x tăng lên mà giá trị tương ứng f(x) cũng tăng lên thì hàm số y = f(x) được gọi là hàm số đồng biến trên R.

Ngược lại thì hàm số nghịch biến trên R.

Trả lời:

a) Ta có bảng giá trị của hai hàm số $y=2x$ và $y=-2x$ là : 

a) Ta có bảng giá trị của hai hàm số $y=2x$ và $y=-2x$ là : 

Vẽ đường thẳng đi qua gốc tọa độ $O\left(0;0\right)$ và điểm $A\left(1;2\right)$ ta được đồ thị hàm số y = 2x

Vẽ đường thẳng đi qua gốc tọa độ $O\left(0;0\right)$ và điểm $B\left(1;-2\right)$ ta được đồ thị hàm số y = - 2x.

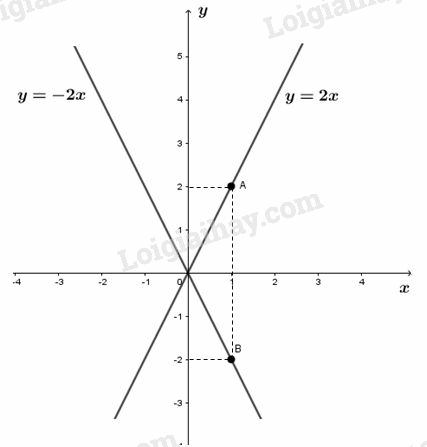
b) Khi giá trị của biến x tăng lên thì giá trị tương ứng của hàm số $y=2x$ cũng tăng lên, do đó hàm số đồng biến trên $\mathbb{R}$.

Khi giá trị của biến x tăng lên thì giá trị tương ứng của hàm số $y=-2x$ lại giảm đi, do đó hàm số nghịch biến trên $\mathbb{R}$.

Bài 3 trang 53 Vở bài tập toán 9 tập 1: Đồ thị hàm số  được vẽ bằng compa và thước thẳng ở hình 2. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
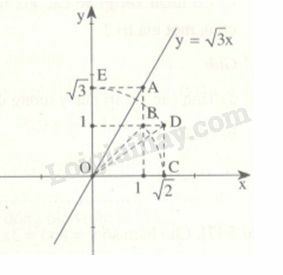Phương pháp giải:

+) Cách vẽ đồ thị hàm số $y=ax,(a\ne 0)$:  Cho $x=x_0\Rightarrow y_0=a{x}_0$

Đồ thị hàm số $y=ax(a\ne 0)$ là đường thẳng đi qua gốc tọa độ và điểm $A(x_0;y_0)$

+) Sử dụng định lí Py-ta-go: Tam giác $\mathrm{\Delta }ABC$ vuông tại $A$ thì $A{B}^2+A{C}^2=B{C}^2$. 

Trả lời

- Vẽ một hình vuông có độ dài cạnh là 1 đơn vị, có một đỉnh là O, đường chéo OB có độ dài bằng $\sqrt{2}.$

- Vẽ cung tròn tâm $O$, bán kính $OB$ , ta xác định được điểm $C$ trên tia $Ox$, và ta có $OC=\sqrt{2}.$

- Vẽ một hình chữ nhật có một đỉnh là O, cạnh $CD=1$ và cạnh  $OC=OB=\sqrt{2}$ ta được đường chéo $OD=\sqrt{C{D}^2+O{C}^2}$$=\sqrt{1+{\left(\sqrt{2}\right)}^2}=\sqrt{3}.$

- Vẽ cung tròn tâm $O$, bán kính $OD$ , ta xác định được điểm $E$ trên tia $Oy$, và ta có $OE=\sqrt{3}.$

- Vẽ hình chữ nhật có một đỉnh là O, có một cạnh bằng 1 đơn vị và một cạnh có độ dài bằng $\sqrt{3}$ ta được điểm $A\left(1;\sqrt{3}\right)$

- Vẽ đường thẳng đi qua gốc tọa độ O và điểm A ta được đồ thị của hàm số $y=\sqrt{3}x$ 

a) Tính giá trị y tương ứng của mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:

b) Có nhận xét gì về các giá trị tương ứng của hai hàm số đó khi biến x lấy cùng một giá trị ?

Phương pháp giải:

a) Thay giá trị của $x$ bằng các số đã cho trong bảng vào $y=0,5x$ và $y=0,5x+2$

     Tính giá trị của biểu thức rồi điền vào ô tương ứng.

b) So sánh giá trị vừa tìm được của hai hàm số rồi kết luận.

Trả lời:

a) Tính giá trị tương ứng của y theo x ta được bảng giá trị sau:

b) Khi biến x lấy cùng một giá trị thì giá trị tương ứng của hàm số $y=0,5x+2$ luôn lớn hơn giá trị tương ứng của hàm số $y=0,5x$ là $2$ đơn vị.