Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 3: Đồ thị của hàm số y=ax+b (a ≠ 0) trang 58,59,60,61,62,63,64 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 3: Đồ thị của hàm số y=ax+b (a ≠ 0)

Phần câu hỏi bài 3 trang 58, 59 Vở bài tập toán 9 tập 1

a) Vẽ đồ thị của các hàm số $y=2x;y=2x+5;y=-{\displaystyle \frac{2}{3}}x;$$y=-{\displaystyle \frac{2}{3}}x+5$ trên cùng một mặt phẳng tọa độ.

b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ?

Phương pháp giải:

a) Cách vẽ đường thẳng $y=ax+b$ (trường hợp $a\ne 0$ và $b\ne 0$)

- Cho $x=0$ thì $y=b,$ được điểm P(0 ; b) thuộc trục tung Oy.

- Cho $y=0$ thì $x=-{\displaystyle \frac{b}{a}}$, được điểm $Q\left(-{\displaystyle \frac{b}{a}};0\right)$ thuộc trục hoành Ox.

- Vẽ đường thẳng đi qua hai điểm P và Q.

b) Vận dụng kiến thức:

- Đồ thị của hàm số $y=ax+b$ $\left(a\ne 0\right)$ là một đường thẳng song song với đường thẳng $y=ax$ nếu $b\ne 0$.

- Nhớ lại các dấu hiệu nhận biết của hình bình hành đã học.

Trả lời:

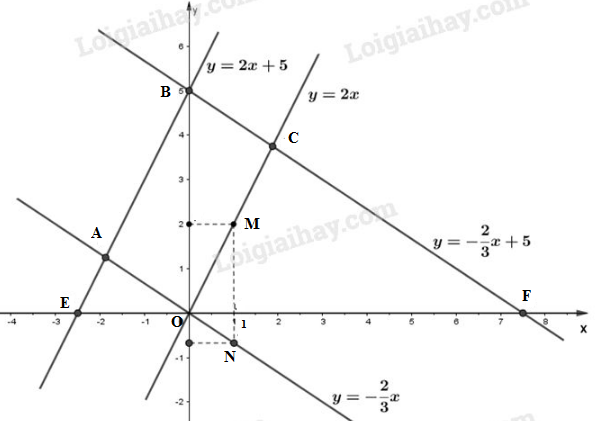
- Vẽ đường thẳng đi qua 2 điểm $O\left(0;0\right)$ và $M\left(1;2\right)$ ta được đồ thị của hàm số $y=2x$.

- Vẽ đường thẳng đi qua hai điểm $O\left(0;0\right)$ và $N\left(1;-{\displaystyle \frac{2}{3}}\right)$ ta được đồ thị của hàm số $y=-{\displaystyle \frac{2}{3}}x$ .

- Vẽ đường thẳng đi qua hai điểm $B\left(0;5\right)$ và $F\left({\displaystyle \frac{15}{2}};0\right)$ ta được đồ thị của hàm số $y=-{\displaystyle \frac{2}{3}}x+5$ .

- Vẽ đường thẳng đi qua hai điểm $B(0;5)$ và $E\left(-{\displaystyle \frac{5}{2}};0\right)$ ta được đồ thị của hàm số $y=2x+5$.

b) Bốn đường thẳng đã cho cắt nhau tạo thành tứ giác OABC. 

Vì đường thẳng $y=2x+5$ song song với đường thẳng $y=2x$ và đường thẳng $y=-{\displaystyle \frac{2}{3}}x+5$ song song với đường thẳng $y=-{\displaystyle \frac{2}{3}}x$ nên tứ giác OABC là hình bình hành ( tứ giác có hai cặp cạnh đối song song).

a) Vẽ đồ thị của các hàm số y = x và y = 2x + 2 trên cùng một mặt phẳng tọa độ.

b) Gọi A là giao điểm của hai đồ thị nói trên, tìm tọa độ điểm A.

c) Vẽ qua điểm B(0 ; 2) một đường thẳng song song với trục Ox, cắt đường thẳng y = x tại điểm C. Tìm tọa độ của điểm C rồi tính diện tích tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét).

Phương pháp giải:

a) Cách vẽ đường thẳng y = ax + b (trường hợp $a\ne 0$ và $b\ne 0$)

- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.

- Cho y = 0 thì $x=-{\displaystyle \frac{b}{a}}$, được điểm $Q\left(-{\displaystyle \frac{b}{a}};0\right)$ thuộc trục hoành Ox.

- Vẽ đường thẳng đi qua hai điểm P và Q.

b) Muốn tìm giao điểm của hai đồ thị hàm số $y=ax+b$ và $y=a^{\prime }x+b^{\prime }$ :

- Giải phương trình: $ax+b=a^{\prime }x+b^{\prime }$ để tìm hoành độ giao điểm.

- Tìm tung độ giao điểm bằng cách thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số đã cho.

c)

- Trên trục tọa độ Oxy lấy điểm $B\left(0;2\right)$ rồi vẽ đường thẳng song song với Ox đi qua điểm B.

- Tìm tọa độ của điểm C.

- Tính diện tích hình tam giác theo công thức : $S_{\mathrm{\Delta }}={\displaystyle \frac{1}{2}}ah$ với $a$ là cạnh đáy và $h$ là chiều cao tương ứng.

Trả lời:

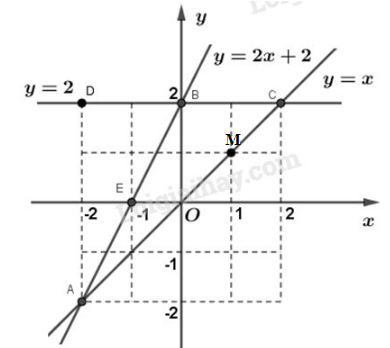
Vẽ đường thẳng đi qua hai điểm $O\left(0;0\right)$ và $M\left(1;1\right)$ ta được đồ thị của hàm số $y=x$.

Vẽ đường thẳng đi qua hai điểm $B\left(0;2\right)$ và $E\left(-1;0\right)$ ta được đồ thị của hàm số $y=2x+2$.

b) Hoành độ giao điểm của hai đồ thị hàm số đã cho là nghiệm của phương trình:

$2x+2=x\iff x=-2$

Thay $x=-2$ vào một trong hai hàm số ta tính được tung độ của A là $y=-2$

Vậy đồ thị hai hàm số đã cho cắt nhau tại $A\left(-2;-2\right)$.

c) Qua điểm $B\left(0;2\right)$ vẽ đường thẳng song song với $Ox$, đường thẳng này có phương trình $y=2$, cắt đường thẳng $y=x$ tại điểm C.

- Tọa độ của điểm C :

Với $y=x$ mà $y=2$ nên $x=2$. Ta có $C\left(2;2\right)$

- Diện tích tam giác ABC:

Tam giác ABC có cạnh đáy là BC và chiều cao là AD.

$BC=2cm$ và $AD=4cm.$

Vậy $S_{ABC}={\displaystyle \frac{1}{2}}BC\cdot AD={\displaystyle \frac{1}{2}}\cdot 2\cdot 4=4\left(c{m}^2\right)$

a) Vẽ đồ thị của các hàm số y = x + 1 và y = -x + 3 trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng y = x + 1 và y = -x + 3 cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ của các điểm A, B, C.

c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet).

Phương pháp giải:

a) Cách vẽ đường thẳng y = ax + b (trường hợp $a\ne 0$ và $b\ne 0$)

- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.

- Cho y = 0 thì $x=-{\displaystyle \frac{b}{a}}$, được điểm $Q\left(-{\displaystyle \frac{b}{a}};0\right)$ thuộc trục hoành Ox.

- Vẽ đường thẳng đi qua hai điểm P và Q.

b) Muốn tìm giao điểm của hai đồ thị hàm số $y=ax+b$ và $y=a^{\prime }x+b^{\prime }$ :

- Giải phương trình: $ax+b=a^{\prime }x+b^{\prime }$ để tìm hoành độ giao điểm.

- Tìm tung độ giao điểm bằng cách thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số đã cho.

Trả lời:

a.

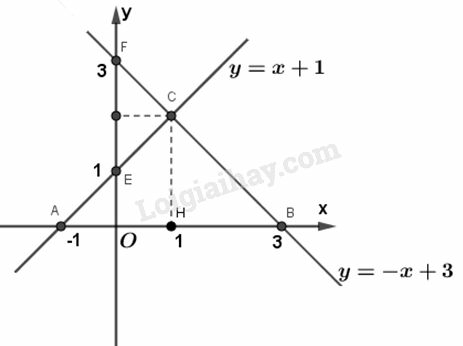
- Vẽ đường thẳng đi qua hai điểm $E\left(0;1\right)$ và $A\left(-1;0\right)$ ta được đồ thị của hàm số $y=x+1$.

- Vẽ đường thẳng đi qua hai điểm $F\left(0;3\right)$ và $B\left(3;0\right)$ thì ta được đồ thị của hàm số $y=-x+3$.

b)

- Đường thẳng $y=x+1$ cắt trục hoành tại điểm $A\left(-1;0\right)$.

- Đường thẳng $y=-x+3$ cắt trục hoành tại điểm $B\left(3;0\right)$.

- Từ $x+1=-x+3$ ta có $x=1$

Thay $x=1$ vào một trong hai hàm số đã cho ta tính được $y=2$

Vậy tọa độ của điểm C là $C\left(1;2\right)$

c)

Gọi P là chu vi của tam giác ABC và S là diện tích của tam giác ABC.

Ta có : $AC=\sqrt{H{A}^2+H{C}^2};BC=\sqrt{H{B}^2+H{C}^2}$

Vậy $P=AC+BC+AB$

           $=\sqrt{2^2+2^2}+\sqrt{2^2+2^2}+4$

           $=4\sqrt{2}+4$

            $=4\left(\sqrt{2}+1\right)\left(cm\right)$

Tính trên máy tính cầm tay ta được $P=4\sqrt{2}+4\approx 9,66\left(cm\right)$

$S={\displaystyle \frac{1}{2}}AB\cdot CH={\displaystyle \frac{1}{2}}\cdot 4\cdot 2=4\left(c{m}^2\right)$

a) Biết rằng với x = 4 thì hàm số y = 3x + b có giá trị là 11. Tìm b. Vẽ đồ thị của hàm số với giá trị b vừa tìm được.

b) Biết rằng đồ thị của hàm số y = ax + 5 đi qua điểm A(-1 ; 3). Tìm a. Vẽ đồ thị của hàm số với giá trị a vừa tìm được. 

Phương pháp giải:

a)

- Thay giá trị của $x=4;y=11$ vào hàm số rồi tìm giá trị của b.

- Vẽ đồ thị hàm số với b vừa tìm được.

b) Thay giá trị của $x=-1;y=3$ vào hàm số đã cho rồi tìm giá trị của a.

    Vẽ đồ thị hàm số với a vừa tìm được.

Trả lời:

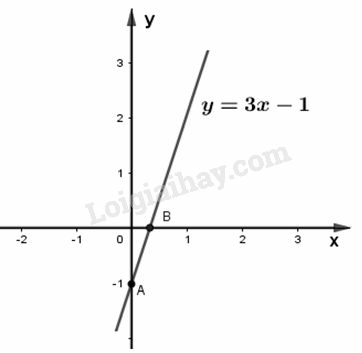
a) Thay $x=4;y=11$ vào hàm số đã cho ta có :

$11=3.4+b\iff b=-1$

Vậy ta có hàm số $y=3x-1$

Cho $x=0$ thì $y=-1$, ta được $A\left(0;-1\right)$

Cho $y=0$ thì $x={\displaystyle \frac{1}{3}}$ , ta được $B\left({\displaystyle \frac{1}{3}};0\right)$.

Vẽ đường thẳng đi qua điểm A và B, ta được đồ thị của hàm số $y=3x-1$.

b) Đường thẳng đi qua điểm $A\left(-1;3\right)$.

Thay giá trị của $x=-1$ và $y=3$ vào hàm số đã cho, ta có:

$3=a.\left(-1\right)+5\iff a=2$

Vậy ta có hàm số $y=2x+5$

Cho $x=0$ thì $y=5$, ta được $D\left(0;5\right)$

Cho $y=0$ thì $x=-{\displaystyle \frac{5}{2}}$ , ta được $C\left(-{\displaystyle \frac{5}{2}};0\right)$.

Vẽ đường thẳng đi qua hai điểm C và D ta được đồ thị của hàm số $y=2x+5$.

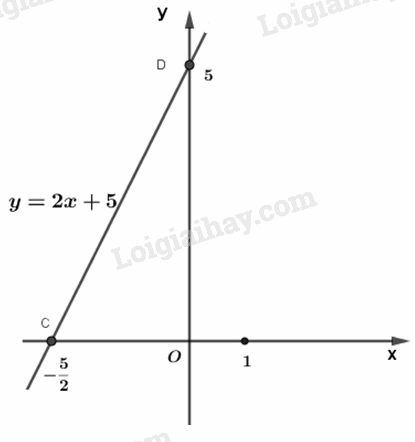
Bài 15 trang 64 Vở bài tập toán 9 tập 1:

Đồ thị của hàm số  được vẽ bằng compa và thước thẳng (h.10a).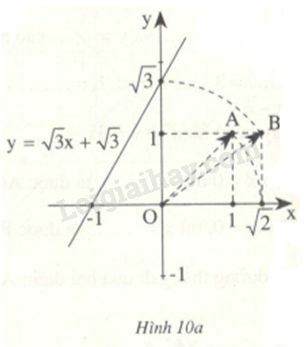

Hãy tìm hiểu cách vẽ đó rồi nêu lại các bước thực hiện.

Áp dụng. Vẽ đồ thị của hàm số $y=\sqrt{5}x+\sqrt{5}$ bằng compa và thước thẳng.

Hướng dẫn. Cách tìm điểm $\sqrt{5}$ trên trục Ox (xem hình 10b).

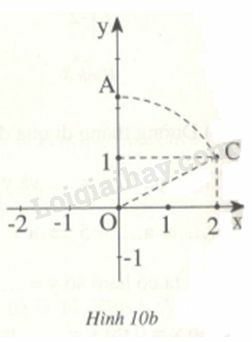
Vẽ hình chữ nhật có một đỉnh là O, cạnh là 1 đơn vị và 2 đơn vị.

Đường chéo của hình chữ nhật là OC có độ dài bằng $\sqrt{1^2+2^2}=\sqrt{5}$

Lấy O làm tâm, quay cung tròn bán kính $OC=\sqrt{5}$, ta xác định được điểm $A\left(0;\sqrt{5}\right)$ 

Phương pháp giải:

+) Xác định hai điểm thuộc đồ thị hàm số $y=ax+b(a\ne 0)$:

   Cho $x=0\Rightarrow y=b\Rightarrow A(0;b).$ 

   Cho $y=0\Rightarrow x=-{\displaystyle \frac{b}{a}}\Rightarrow B\left(-{\displaystyle \frac{b}{a}};0\right).$

Xác định vị trí hai điểm $A,B$ trên mặt phẳng tọa độ. Đường thẳng đi qua $A,B$ là đồ thị hàm số $y=ax+b.$

+) Định lí Py-ta-go trong tam giác vuông: Cho tam giác $ABC$ vuông tại $A$. Khi đó:

              $B{C}^2=A{B}^2+A{C}^2$. 

Trả lời:

* Cách vẽ đồ thị hàm số $y=\sqrt{3}x+\sqrt{3}$

+ Gọi $A\left(1;1\right)$ thì $OA=\sqrt{1^2+1^2}=\sqrt{2}$

+ Lấy điểm C trên Ox có tọa độ $C\left(\sqrt{2};0\right)$ và gọi $B\left(\sqrt{2};1\right)$. Khi đó $OB=\sqrt{{\left(\sqrt{2}\right)}^2+1^2}=\sqrt{3}$

Dùng compa dựng cung tròn $O\left(0;\sqrt{3}\right)$ cắt trục tung tại điểm có tọa độ $(0;\sqrt{3})$

Đồ thị hàm số $y=\sqrt{3}x+\sqrt{3}$ là đường thẳng qua hai điểm có tọa độ $\left(0;\sqrt{3}\right)$ và $\left(-1;0\right)$

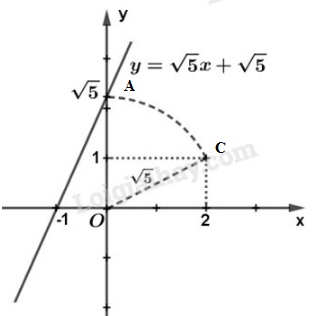
* Vẽ đồ thị hàm số $y=\sqrt{5}x+\sqrt{5}$ (làm tương tự như trên)

    Cho $x=0\Rightarrow y=\sqrt{5}.0+\sqrt{5}=\sqrt{5}\Rightarrow B(0;\sqrt{5})$.

    Cho $x=-1\Rightarrow y=\sqrt{5}.(-1)+\sqrt{5}=0\Rightarrow C(-1;0)$.

Bước $1$: Xác định điểm $C(2;1)$ trên mặt phẳng tọa độ $Oxy$.

           Áp dụng định lí Py-ta-go, ta có:

             $O{C}^2=2^2+1^2=4+1=5\iff OC=\sqrt{5}$

Bước $2$: Vẽ cung tròn tâm $O$ bán kính $OC=\sqrt{5}$. Cung tròn này cắt trục $Oy$ tại vị trí điểm $A$ có tung độ là $\sqrt{5}$. Ta xác định được điểm $A$.

Bước $3$: Kẻ đường thẳng đi qua hai điểm $A(0;\sqrt{5})$ và $(-1;0)$ ta được đồ thị của hàm số $y=\sqrt{5}x+\sqrt{5}$.

Hình vẽ: