Trả lời câu hỏi giữa bài
Trả lời câu hỏi 1 trang 53 SGK Toán 9 Tập 1: a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
b) Giải thích vì sao hai đường thẳng và song song với nhau ? (h.9)
Phương pháp giải:
Chú ý: Hai đường thẳng song song là hai đường thẳng không có điểm chung
Lời giải:
a)
b) Ta thấy hai đường thẳng trên không có điểm chung nên chúng song song với nhau.
Trả lời câu hỏi 2 trang 53 SGK Toán 9 Tập 1: Tìm các cặp đường thẳng cắt nhau trong các đường thẳng sau:
y = 0,5x + 2;
y = 0,5x - 1;
y = 1,5x + 2.
Phương pháp giải:
Vẽ đồ thị các hàm số rồi quan sát hình vẽ.
Lời giải:
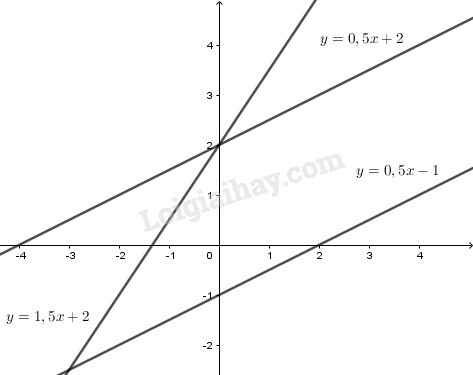
Các cặp đường thẳng cắt nhau là:
y = 0,5x + 2 và y = 1,5x +2
y = 0,5x - 1 và y = 1,5x +2
Bài tập trang 54-55 SGK Toán 9
Bài 20 trang 54 sgk Toán 9 tập 1: Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau:
a) ; b) ;
c) ; d) ;
e) ; g) .
Phương pháp giải:
+ Cho hai đường thẳng: : , và : . Khi đó:
// và
cắt
trùng và
Lời giải:
Ba cặp đường thẳng song song:
+ và
và
Vì nên song song với .
+ và
và
Vì nên song song với .
+ và
và
Vì nên song song với .
Ba cặp đường thẳng cắt nhau là:
+
Vì nên và cắt nhau.
+
Vì nên và cắt nhau.
+
Vì nên và cắt nhau.
Bài 21 trang 54 sgk Toán 9 tập 1: Cho hàm số bậc nhất
và
. Tìm giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau;
b) Hai đường thẳng cắt nhau.
Phương pháp giải:
a) + Điều kiện để hàm số đã cho là hàm bậc nhất là .
+ Hai đường thẳng: : , và : song song khi và chỉ khi và
b) + Điều kiện để hàm số đã cho là hàm bậc nhất là .
+ Hai đường thẳng: : , và : cắt nhau khi và chỉ khi
Lời giải:
Ta có:
+
+
+ Để hai hàm số đã cho là hàm bậc nhất thì ta cần có các hệ số và khác , tức là:
a) Để hai đường thẳng song song thì:
Vậy thì hai đường thẳng trên song song với nhau.
b) Để hai đường thẳng cắt nhau thì:
Kết hợp với điều kiện trên, ta có thì hai đường thẳng trên cắt nhau.
Bài 22 trang 55 sgk Toán 9 tập 1: Cho hàm số . Hãy xác định hệ số a trong mỗi trường hợp sau:
a) Đồ thị của hàm số song song với đường thẳng .
b) Khi thì hàm số có giá trị
Phương pháp giải:
a) Đồ thị hàm số song song với đồ thị hàm số thì và .
b) Thay các giá trị vào công thức hàm số ta tìm được .
Lời giải:
a) Ta có:
Đồ thị hàm số và song song với nhau
Vậy .
b)
Thay , và vào công thức hàm số , ta được:
Vậy .
Bài 23 trang 55 sgk Toán 9 tập 1: Cho hàm số . Hãy xác định hệ số trong mỗi trường hợp sau:
a) Đồ thị của hàm số đã cho cắt trục tung tại điểm có tung độ bằng ;
b) Đồ thị của hàm số đã cho đi qua điểm .
Phương pháp giải:
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng thì đồ thị hàm số đi qua điểm . Thay tọa độ vào công thức hàm số tìm được .
b) Thay tọa độ điểm vào công thức hàm số ta tìm được .
Lời giải:
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng , nghĩa là đồ thị hàm số đi qua điểm . Thay vào công thức hàm số , ta được:
Vậy .
b) Vì đồ thị của hàm số đã cho đi qua điểm nên thay vào công thức hàm số , ta được:
Vậy .
Bài 24 trang 55 sgk Toán 9 tập 1: Cho hai hàm số bậc nhất và .
Tìm điều kiện đối với và để đồ thị của hai hàm số là:
a) Hai đường thẳng cắt nhau;
b) Hai đường thẳng song song với nhau;
c) Hai đường thằng trùng nhau.
Phương pháp giải:
+) Điều kiện để hàm số là hàm số bậc nhất là
+) Hai đường thẳng: : , và : :
cắt
// và
và
Lời giải:
Ta có:
Hai hàm số đã cho là hàm bậc nhất khi và chỉ khi:
a) Hai đường thẳng cắt nhau:
cắt
Kết hợp điều kiện hàm bậc nhất .
b) Hai đường thẳng song song:
Vậy và thì hai đồ thị trên song song.
c) Hai đường thẳng trùng nhau:
Vậy và thì đồ thị hai hàm số trên trùng nhau.
Bài 25 trang 55 sgk Toán 9 tập 1: a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
;
b) Một đường thẳng song song với trục hoành , cắt trục tung tại điểm có tung độ bằng , cắt các đường thẳng và theo thứ tự tại hai điểm và . Tìm tọa độ của hai điểm và .
Phương pháp giải:
a) Cách vẽ đồ thị hàm số : Đồ thị hàm số là đường thẳng:
+) Cắt trục hoành tại điểm
+) Cắt trục tung tại điểm
Xác định tọa độ hai điểm và sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số
b) +) Đường thẳng song song với trục có dạng , đường thẳng song song với trục có dạng .
+) Hai đường thẳng cắt nhau tại . Hoành độ điểm là nghiệm của phương trình: . Giải phương trình tìm . Thay tìm được vào công thức hàm số trên tìm được tung độ điểm .
Lời giải:
a) Hàm số
Cho
Cho
Đường thẳng đi qua hai điểm là đồ thị của hàm số .
+) Hàm số
Cho
Cho
Đường thẳng đi qua hai điểm là đồ thị của hàm số .
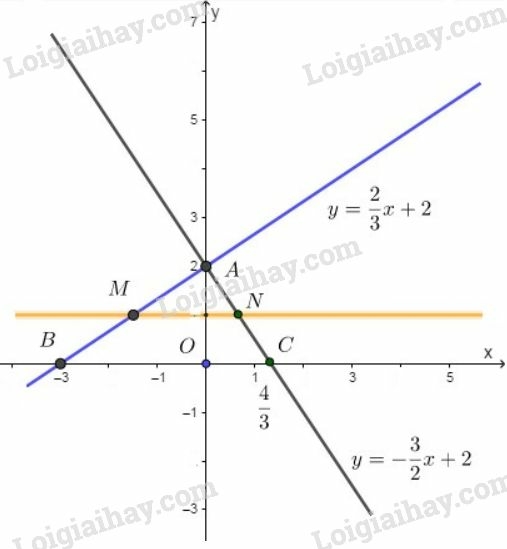
b) Đường thẳng song song với trục cắt trục tại điểm có tung độ có dạng: .
Vì là giao của đường thẳng và nên hoành độ của là nghiệm của phương trình:
Do đó tọa độ là: .
Vì là giao của đường thẳng và nên hoành độ của là nghiệm của phương trình:
Do đó tọa độ là: .
Bài 26 trang 55 sgk Toán 9 tập 1: Cho hàm số bậc nhất
(1). Hãy xác định hệ số
trong mỗi trường hợp sau:
a) Đồ thị của hàm số cắt đường thẳng tại điểm có hoành độ bằng .
b) Đồ thị của hàm số cắt đường thẳng tại điểm có tung độ bằng . Phương pháp giải:
a) Cho hai hàm số bậc nhất . Xét phương trình hoành độ giao điểm:
Thay hoành độ giao điểm vào phương trình , ta tìm được .
b) Thay tung độ giao điểm vào phương trình hàm số đã biết các hệ số ta tìm được tọa độ giao điểm.
Thay tọa độ giao điểm vừa tìm được vào phương trình hàm số ban đầu ta tìm được .
Lời giải:
a) Xét phương trình hoành độ giao điểm của hai đường thẳng và là: .
Đồ thị hàm số cắt đường thẳng tại điểm có hoành độ bằng 2 nên thay vào phương trình hoành độ giao điểm trên, ta có:
.
b) Ta có:
Đồ thị hàm số cắt đường thẳng tại điểm có tung độ bằng nên đường thẳng đi qua điểm có tung độ bằng
Thay tung độ giao điểm vào phương trình , ta được:
Do đó hoành độ giao điểm là . Thay vào phương trình , ta được:
Vậy .
Lý thuyết Toán 9 Bài 4: Đường thẳng song song và đường thẳng cắt nhau.
I. Vị trí tương đối của hai đường thẳng
Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng và .
+)
+) cắt .
+) .
Ngoài ra, .
Ví dụ:
Hai đường thẳng và có hệ số và nên chúng song song với nhau.
Hai đường thẳng và có hệ số và nên chúng trùng nhau.
Hai đường thẳng và có hệ số nên chúng cắt nhau.
II. Các dạng toán thường gặp
Dạng 1: Chỉ ra vị trí tương đối của hai đường thẳng cho trước. Tìm tham số để các đường thẳng thỏa mãn vị trí tương đối cho trước.
Phương pháp:
Cho hai đường thẳng và .
+)
+) cắt .
+) .
Dạng 2: Viết phương trình đường thẳng
Phương pháp:
+) Sử dụng vị trí tương đối của hai đường thẳng để xác định hệ số.
Ngoài ra ta còn sử dụng các kiến thức sau
+) Ta có với , là phương trình đường thẳng cắt trục tung tại điểm , cắt trục hoành tại điểm .+) Điểm thuộc đường thẳng khi và chỉ khi .
Dạng 3: Tìm điểm cố định mà đường thẳng luôn đi qua với mọi tham số
Phương pháp:
Gọi là điểm cần tìm khi đó tọa độ điểm thỏa mãn phương trình đường thẳng .
Đưa phương trình đường thẳng về phương trình bậc nhất ẩn .
Từ đó để phương trình bậc nhất luôn đúng thì
Giải điều kiện ta tìm được .
Khi đó là điểm cố định cần tìm.
