Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 4: Đường thẳng song song và đường thẳng cắt nhau trang 65,66,67,68,69 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Bài 4: Đường thẳng song song và đường thẳng cắt nhau

Phần câu hỏi bài 4 trang 65 Vở bài tập toán 9 tập 1

Cho hai hàm số bậc nhất $y=mx+3$ và $y=\left(2m+1\right)x-5$. Tìm giá trị của m để đồ thị của hai hàm số đã cho là:

a) Hai đường thẳng song song với nhau.

b)  Hai đường thẳng cắt nhau.

Phương pháp giải:

Vận dụng kiến thức :

+ Hàm số $y=ax+b$ là hàm số bậc nhất khi $a\ne 0$

+ Hai đường thẳng $y=ax+b\left(a\ne 0\right)$ và $y=a^{\prime }x+b^{\prime }\left(a^{\prime }\ne 0\right)$

a) Song song với nhau khi $a=a^{\prime }$ và $b\ne b^{\prime }$

b) Cắt nhau khi $a\ne a^{\prime }$.

Trả lời:

Hai hàm số đã cho là hàm số bậc nhất khi :

$m\ne 0$ và $2m+1\ne 0$ 

$\iff m\ne 0$ và $m\ne -{\displaystyle \frac{1}{2}}$    (1)

a) Hai đường thẳng đã cho song song với nhau khi $m=2m+1\iff m=-1$    (2)

Từ các điều kiện (1) và (2) ta có kết luận :

Hai hàm số bậc nhất đã cho có đồ thị là hai đường thẳng song song với nhau khi $m=-1$

b) Hai đường thẳng đã cho cắt nhau khi $m\ne 2m+1\iff m\ne -1$.        (3)

Từ (1) và (3) ta có kết luận:

Hai hàm số đã cho là hai hàm số bậc nhất và có đồ thị là hai đường thẳng cắt nhau khi $m\ne 0$,$m\ne -{\displaystyle \frac{1}{2}}$ và $m\ne -1$ .

Cho hàm số $y=ax+3$. Hãy xác định hệ số a trong mỗi trường hợp sau:

a) Đồ thị của hàm số song song với đường thẳng $y=-2x$

b) Khi x = 2 thì hàm số có giá trị y = 7.

Phương pháp giải:

a) Hai đường thẳng $y=ax+b\left(a\ne 0\right)$ và $y=a^{\prime }x+b^{\prime }\left(a^{\prime }\ne 0\right)$ song song với nhau khi $a=a^{\prime }$ và $b\ne b^{\prime }$.

b) Thay giá trị $x=2;y=7$ vào hàm số rồi tìm giá trị của a.

Trả lời:

a) Hệ số b và b’ của hai hàm số $y=ax+3$ và $y=-2x$ đã khác nhau ( $b=3$ và $b^{\prime }=0$ ), do đó, hai đường thẳng này song song với  nhau khi các hệ số a và a’ của x bằng nhau:

Vậy $a=-2$.

b) Theo giả thiết, khi x = 2 thì hàm số có giá trị y = 7, do đó ta có :

$7=a\cdot 2+3\iff a=2$.

Cho hàm số $y=2x+b$. Hãy xác định hệ số b trong mỗi trường hợp sau:

a) Đồ thị của hàm số đã cho cắt trục tung tại điểm có tung độ bằng -3;

b) Đồ thị của hàm số đã cho đi qua điểm A(1 ; 5).

Phương pháp giải:

a) Thay $x=0;y=-3$ vào hàm số đã cho để tìm b.

b) Thay $x=1;y=5$ vào hàm số đã cho để tìm b.

Trả lời:

a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng $-3$, nghĩa là đồ thị hàm số đi qua điểm $M(0;-3)$. Thay $x=0;y=-3$ vào công thức hàm số $y=2x+b$, ta được:

 $-3=2.0+b\iff -3=0+b$$\iff b=-3$

Vậy $b=-3$.

b) Thay $x=1;y=5$ vào công thức hàm số, ta được:

$5=2.1+b\iff 5=2+b$

$\iff 5-2=b$

$\iff b=3$

Vậy $b=3$. 

Cho hai hàm số bậc nhất $y=2x+3k$ và $y=\left(2m+1\right)x+2k-3$

Tìm điều kiện đối với m và k để đồ thị của hai hàm số là:

a) Hai đường thẳng cắt nhau.

b) Hai đường thẳng song song với nhau.

c) Hai đường thẳng trùng nhau.

Phương pháp giải:

- Tìm điều kiện để hàm số đã cho là hàm số bậc nhất.

- Vận dụng kiến thức: Hai đường thẳng $y=ax+b\left(a\ne 0\right)$ và $y=a^{\prime }x+b^{\prime }\left(a^{\prime }\ne 0\right)$

- Cắt nhau khi $a\ne a^{\prime }$

- Song song với nhau khi $a=a^{\prime }$ và $b\ne b^{\prime }$

- Trùng nhau khi $a=a^{\prime }$ và $b=b^{\prime }$

Trả lời:

a) Do $y=\left(2m+1\right)x+2k-3$ là hàm số bậc nhất nên hệ số của x phải khác 0, nghĩa là $2m+1\ne 0\iff m\ne -{\displaystyle \frac{1}{2}}$ .

Hai đường thẳng $y=2x+3k$ và $y=\left(2m+1\right)x+2k-3$ cắt nhau khi và chỉ khi: $2m+1\ne 2\iff m\ne {\displaystyle \frac{1}{2}}$

Vậy điều kiện đối với m là : $m\ne -{\displaystyle \frac{1}{2}}$  và $m\ne {\displaystyle \frac{1}{2}}$ , $k$ tùy ý.

b) Hai đường thẳng $y=2x+3k$ và $y=\left(2m+1\right)x+2k-3$ song song với nhau khi :

$\{\begin{array}{l}2m+1\ne 0\\ 2m+1=2\\ 2k-3\ne 3k\end{array}$

$2m+1\ne 0\iff m\ne -{\displaystyle \frac{1}{2}}$

$2m+1=2\iff m={\displaystyle \frac{1}{2}}$

$2k-3\ne 3k\iff k\ne -3$

Vậy hai đường thẳng đã cho song song với nhau khi $m={\displaystyle \frac{1}{2}}$ và $k\ne -3$.

c) Hai đường thẳng $y=2x+3k$ và $y=\left(2m+1\right)x+2k-3$ trùng nhau khi :

$\{\begin{array}{l}2m+1\ne 0\\ 2m+1=2\\ 2k-3=3k\end{array}$$\iff \{\begin{array}{l}m\ne -{\displaystyle \frac{1}{2}}\\ m={\displaystyle \frac{1}{2}}\\ k=-3\end{array}$

Vậy hai đường thẳng đã cho trùng nhau khi $m={\displaystyle \frac{1}{2}}$ và$k=-3$.

Bài 20 trang 68 Vở bài tập toán 9 tập 1

a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

$y={\displaystyle \frac{2}{3}}x+2;y=-{\displaystyle \frac{3}{2}}x+2$

b) Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt các đường thẳng $y={\displaystyle \frac{2}{3}}x+2$ và $y=-{\displaystyle \frac{3}{2}}x+2$ theo thứ tự tại hai điểm M và N. Tìm tọa độ của hai điểm M và N.

Phương pháp giải:

a) Vẽ đồ thị của hai hàm số đã cho:

- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.

- Cho y = 0 thì $x=-{\displaystyle \frac{b}{a}}$, được điểm $Q\left(-{\displaystyle \frac{b}{a}};0\right)$ thuộc trục hoành Ox.

b) Vẽ đường thẳng đi qua điểm có tọa độ $\left(0;1\right)$và song song với Ox; cắt các đường thẳng của hai hàm số đã vẽ ở câu a lần lượt tại M và N.

Tìm tọa độ giao điểm M và N :

- Xác định tung độ của giao điểm.

- Thay tung độ giao điểm vào một hàm số đã biết để tìm giá trị của hoành độ.

Trả lời:

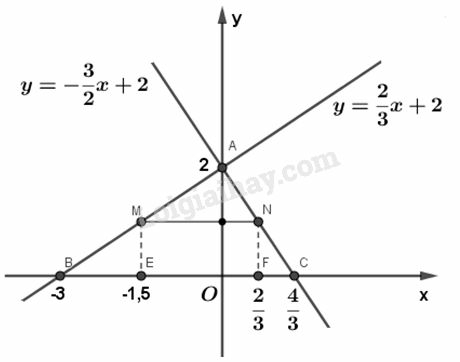
a) Vẽ đồ thị hàm số $y={\displaystyle \frac{2}{3}}x+2$:

+) Cho $x=0$ thì $y=2$, được điểm $A\left(0;2\right)$

+) Cho $y=0$ thì $x=-3$ , được điểm $B\left(-3;0\right)$

Vẽ đường thẳng đi qua hai điểm A và B, được đồ thị của hàm số $y={\displaystyle \frac{2}{3}}x+2$

Vẽ đồ thị của hàm số $y=-{\displaystyle \frac{3}{2}}x+2$

+) Cho $x=0$ thì $y=2$ , được điểm $A\left(0;2\right)$

+) Cho $y=0$ thì $x={\displaystyle \frac{4}{3}}$ , được điểm $C\left({\displaystyle \frac{4}{3}};0\right)$

Vẽ đường thẳng đi qua hai điểm A và C, được đồ thị của hàm số $y=-{\displaystyle \frac{3}{2}}x+2$.

b) Tọa độ của điểm M :

Điểm M có tung độ $y=1$

Thay giá trị $y=1$  vào phương trình $y={\displaystyle \frac{2}{3}}x+2$ để tìm x, ta có :

$1={\displaystyle \frac{2}{3}}x+2\Rightarrow {\displaystyle \frac{2}{3}}x=-1\Rightarrow x=\left(-1\right):{\displaystyle \frac{2}{3}}=-{\displaystyle \frac{3}{2}}$

Vậy ta có $M\left(-{\displaystyle \frac{3}{2}};1\right)$

Tọa độ của điểm N :

Điểm N có tung độ $y=1$

Thay giá trị $y=1$ vào phương trình $y=-{\displaystyle \frac{3}{2}}x+2$ để tìm x, ta có :

$1=-{\displaystyle \frac{3}{2}}x+2\Rightarrow {\displaystyle \frac{3}{2}}x=1\Rightarrow x={\displaystyle \frac{2}{3}}$

Vậy ta có : $N\left({\displaystyle \frac{2}{3}};1\right)$

Cho hàm số bậc nhất $y=ax-4\left(1\right)$. Hãy xác định hệ số a trong mỗi trường hợp sau:

a) Đồ thị của hàm số (1) cắt đường thẳng $y=2x-1$ tại điểm có hoành độ bằng 2.

 b) Đồ thị của hàm số (1) cắt đường thẳng $y=-3x+2$ tại điểm có tung độ bằng 5.

Phương pháp giải:

a) Thay giá trị $x=2$ vào hai hàm số và cho giá trị hai hàm số đó bằng nhau, giải và tìm a.

b) Tìm hoành độ giao điểm của hai đường thẳng rồi thay giải tương tự câu a.

Trả lời

a) Hai đường thẳng $y=ax-4$ và $y=2x-1$ cắt nhau tại điểm có hoành độ bằng $2$ nên tại $x=2$, giá trị của hai hàm số bằng nhau.

Do đó, thay $x=2$ vào hai hàm số ta có :

$a.2-4=2.2-1\iff 2a=3+4$ $\iff a={\displaystyle \frac{7}{2}}$

b) Hai đường thẳng $y=ax-4$ và $y=-3x+2$ cắt nhau tại điểm N có tung độ bằng $5$. Giả sử hoành độ của giao điểm N là $x_0$. Ta có $N\left(x_0;5\right)$ .

Vì đường thẳng $y=-3x+2$ đi qua $N\left(x_0;5\right)$ nên ta có :

$5=-3x_0+2$ $\iff 3=-3x_0\iff x_0=-1$

Vì đường thẳng $y=ax-4$ cũng đi qua điểm $N\left(-1;5\right)$ nên ta có :

$5=a.\left(-1\right)-4$ $\iff a=-9$

Chú ý:

Để giải các bài toán tìm tọa độ giao điểm của hai đường thẳng $y=ax+b$ và $y=a^{\prime }x+b^{\prime }$ , ta cần chú ý rằng : Tọa độ $\left(x_0;y_0\right)$ của giao điểm phải thỏa mãn các phương trình của hai hàm số.

Do đó, khi đã biết hoành độ $x_0$ (hoặc tung độ $y_0$) ta chỉ việc thay các giá trị $x_0$ (hoặc $y_0$) vào một trong hai hàm số đã cho để tìm nốt giá trị còn lại $y_0$ (hoặc $x_0$)