Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Ôn tập chương 2-Hàm số bậc nhất trang 75,76,77,78,79  chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Ôn tập chương 2-Hàm số bậc nhất

Bài 27 trang 75 Vở bài tập toán 9 tập 1

a) Với những giá trị nào của m thì hàm số bậc nhất $y=\left(m-1\right)x+3$ đồng biến ?

b) Với những giá trị nào của k thì hàm số bậc nhất $y=\left(5-k\right)x+1$ nghịch biến ?

Phương pháp giải:

Vận dụng kiến thức : Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:

a) Đồng biến trên R khi a > 0

b) Nghịch biến trên R khi a < 0

Trả lời:

a) Hàm số $y=\left(m-1\right)x+3$ là hàm số bậc nhất, do đó

$m-1\ne 0\iff m\ne 1$              (1)

$y=\left(m-1\right)x+3$ đồng biến khi $m-1>0\iff m>1$               (2)

Kết hợp (1) và (2), suy ra hàm số đã cho đồng biến khi $m>1$.

b) Hàm số $y=\left(5-k\right)x+1$ là hàm số bậc nhất, do đó $5-k\ne 0\iff k\ne 5$         (3)

$y=\left(5-k\right)x+1$ nghịch biến khi $5-k<0\iff k>5$              (4)

Kết hợp (3) và (4), suy ra hàm số đã cho nghịch biến khi $k>5$.

Với những giá trị nào của m thì đồ thị các hàm số $y=2x+\left(3+m\right)$ và $y=3x+\left(5-m\right)$ cắt nhau tại một điểm trên trục tung ?

Phương pháp giải:

Đồ thị hai hàm số cắt nhau tại một điểm trên trục tung khi tung độ gốc của chúng bằng nhau và hệ số góc của chủng khác nhau.

Trả lời:

Hai đường thẳng $y=2x+\left(3+m\right)$ và $y=3x+\left(5-m\right)$ cắt nhau tại một điểm trên trục tung khi và chỉ khi $3+m=5-m$ $\iff m=1$

Tìm giá trị của a để hai đường thẳng $y=\left(a-1\right)x+2\left(a\ne 1\right)$ và $y=\left(3-a\right)x+1\left(a\ne 3\right)$ song song với nhau ?

Phương pháp giải:

Vận dụng kiến thức : Hai đường thẳng y= ax+b (a ≠ 0) và y= a'x+ b' (a' ≠ 0) song song với nhau khi a=a' và b ≠ b

Trả lời

Tung độ gốc của hai đường thẳng đã cho là khác nhau $\left(2\ne 1\right)$, do đó hai đường thẳng này song song với nhau khi

$a-1=3-a\iff a=2$

$a=2$ thỏa mãn hai điều kiện khác $1$ và khác $3$.

Vậy khi $a=2$ thì hai đường thẳng đã cho song song với nhau.

Xác định k và m để hai đường thẳng sau đây trùng nhau:

$y=kx+\left(m-2\right),\left(k\ne 0\right);y=\left(5-k\right)x+\left(4-m\right),\left(k\ne 5\right)$

Phương pháp giải:

Hai đường thẳng y= ax+b (a ≠ 0) và y= a'x+ b (a' ≠ 0)  trùng nhau khi a=a' và b=b' .
Trả lời:

Hai đường thẳng đã cho trùng nhau khi $k=5-k$ và $m-2=4-m$

Từ đó ta có $k={\displaystyle \frac{5}{2}}$ và $m=3$, thỏa mãn các điều kiện $k\ne 0$ và $k\ne 5$.

Vậy hai đường thẳng đã cho trùng nhau khi  $k={\displaystyle \frac{5}{2}}$ và $m=3$.

ho hai hàm số bậc nhất $y=\left(k+1\right)x+3$ và $y=\left(3-2k\right)x+1$

a) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng song song ?

b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau ?

c) Hai đường thẳng nói trên có thể trùng nhau được không ? Vì sao ? 

Phương pháp giải:

Vận dụng kiến thức: Hai đường thẳng $y=ax+b\left(a\ne 0\right)$ và $y=a^{\prime }x+b^{\prime }\left(a^{\prime }\ne 0\right)$

- Cắt nhau khi $a\ne a^{\prime }$

- Song song với nhau khi $a=a^{\prime }$ và $b\ne b^{\prime }$

- Trùng nhau khi $a=a^{\prime }$ và $b=b^{\prime }$

Trả lời:

$y=\left(k+1\right)x+3$ là hàm số bậc nhất, do đó $k+1\ne 0$ $\iff k\ne -1$

$y=\left(3-2k\right)x+1$ là hàm số bậc nhất, do đó $3-2k\ne 0\iff k\ne {\displaystyle \frac{3}{2}}$

a) Hai đường thẳng đã cho có các tung độ gốc khác nhau $\left(1\ne 3\right)$, do đó chúng song song với nhau khi:

$k+1=3-2k\iff k={\displaystyle \frac{2}{3}}$

$k={\displaystyle \frac{2}{3}}$ thỏa mãn điều kiện khác $-1$ và khác ${\displaystyle \frac{3}{2}}$ .

Vậy khi $k={\displaystyle \frac{2}{3}}$ thì hai đường thẳng đã cho song song với nhau.

b) Hai đường thẳng đã cho cắt nhau khi :

$k+1\ne 3-2k\iff k\ne {\displaystyle \frac{2}{3}}$

Kết hợp với điều kiện $k\ne -1$ và $k\ne {\displaystyle \frac{3}{2}}$ , ta có thể trả lời :

Khi $k\ne -1,k\ne {\displaystyle \frac{3}{2}}$ và $k\ne {\displaystyle \frac{2}{3}}$ thì hai đường thẳng đã cho song song với nhau.

c) Hai đường thẳng $y=\left(k+1\right)x+3$ và $y=\left(3-2k\right)x+1$ không bao giờ trùng nhau vì tung độ gốc khác nhau $\left(1\ne 3\right)$.

Bài 32 trang 77 Vở bài tập toán 9 tập 1

a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ:

y = 0,5x + 2                 (1)

y = 5 – 2x                    (2)

b) Gọi giao điểm của các đường thẳng y = 0,5x + 2 và y = 5 – 2x với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.

Tìm tọa độ của các điểm A, B, C

c) Tính độ dài các đoạn AB, AC và BC (đơn vị đi trên các trục tọa độ là xentimet) (làm tròn đến chữ số thấp phân thứ hai).

d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).

Phương pháp giải:

a) Cách vẽ đường thẳng y = ax + b (trường hợp $a\ne 0$ và $b\ne 0$)

- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.

- Cho y = 0 thì $x=-{\displaystyle \frac{b}{a}}$, được điểm $Q\left(-{\displaystyle \frac{b}{a}};0\right)$ thuộc trục hoành Ox.

- Vẽ đường thẳng đi qua hai điểm P và Q. 

b) Tìm hoành độ giao điểm rồi thay vào một trong hai hàm số để tìm giá trị của tung độ giao điểm.

Trả lời:

a) Vẽ đồ thị hàm số $y=0,5x+2$ :

Cho $x=0$ thì $y=2$, được điểm $D\left(0;2\right)$

Cho $y=0$ thì $x=-4$, được điểm $A\left(-4;0\right)$

Vẽ đường thẳng đi qua hai điểm A, D được đồ thị hàm số $y=0,5x+2$.

- Vẽ đồ thị hàm số $y=5-2x$ :

Cho $x=0$ thì $y=5$, được điểm $E\left(0;5\right)$

Cho $y=0$ thì $x={\displaystyle \frac{5}{2}}$, được điểm $B\left({\displaystyle \frac{5}{2}};0\right)$

Vẽ đường thẳng đi qua hai điểm B, E, được đồ thị hàm số $y=5-2x$.

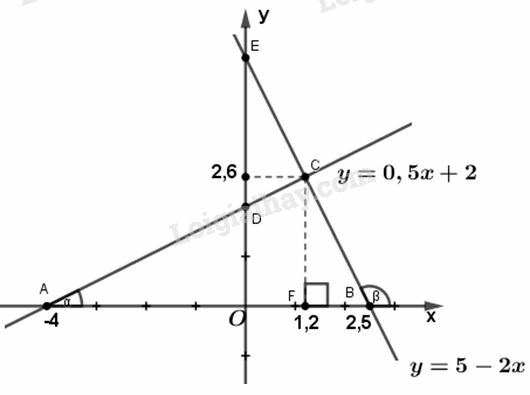
b) Ở câu a) đã tính được tọa độ của hai điểm A và B là $A\left(-4;0\right)$ và $B\left({\displaystyle \frac{5}{2}};0\right)$.

Ta tìm tọa độ của điểm C :

- Tìm hoành độ của điểm C:

$0,5x+2=5-2x\iff x={\displaystyle \frac{6}{5}}$

- Tìm tung độ của điểm C (thay $x={\displaystyle \frac{6}{5}}$ vào một trong hai hàm số), ta có :

$y=0,5\cdot {\displaystyle \frac{6}{5}}+2={\displaystyle \frac{13}{5}}$

Vậy ta có : $C\left({\displaystyle \frac{6}{5}};{\displaystyle \frac{13}{5}}\right)$

c) $AB=AO+OB$$=\left|-4\right|+\left|2,5\right|=6,5$

Gọi F là hình chiếu của C trên Ox, ta có $\mathrm{O}\mathrm{F}=1,2\left(cm\right)$, $\mathrm{A}\mathrm{F}=5,2\left(cm\right)$, $BF=1,3\left(cm\right)$.

Áp dụng định lí Py-ta-go vào các tam giác vuông ACF và BCF, ta có :

$AC=\sqrt{A{F}^2+C{F}^2}=\sqrt{5,2^2+2,6^2}$ $\approx 5,8\left(cm\right)$

$BC=\sqrt{B{F}^2+C{F}^2}=\sqrt{1,3^2+2,6^2}$$\approx 2,9\left(cm\right)$

d) Gọi $\alpha$ là góc tạo bởi đường thẳng $y=0,5x+2$ và trục Ox, ta có :

$\tan \alpha =0,5\Rightarrow \alpha \approx {26}^o{33}^{\prime }$

Gọi $\beta$ là góc tạo bởi đường thẳng $y=5-2x$ với trục $\mathrm{O}\mathrm{x}$, ta có :

$\tan \left({180}^o-\beta \right)=\left|-2\right|$$\Rightarrow {180}^o-\beta \approx {63}^o{26}^{\prime }$ $\Rightarrow \beta \approx {180}^o-{63}^o{26}^{\prime }\approx {116}^o{34}^{\prime }$.

a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:

y = 2x              (1)

y = 0,5x           (2)

y = -x + 6        (3)

b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.

c) Tính các góc của tam giác OAB.

Phương pháp giải:

a) Cách vẽ đường thẳng y = ax + b (trường hợp $a\ne 0$ và $b\ne 0$)

- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.

- Cho y = 0 thì $x=-{\displaystyle \frac{b}{a}}$, được điểm $Q\left(-{\displaystyle \frac{b}{a}};0\right)$ thuộc trục hoành Ox.

- Vẽ đường thẳng đi qua hai điểm P và Q.

b) Tìm hoành độ giao điểm rồi thay vào một trong hai hàm số để tìm giá trị của tung độ giao điểm.

c)

-  Chứng minh tam giác đã cho là tam giác cân.

- Tìm độ lớn của góc ở đỉnh.

- Tìm độ lớn hai góc kề cạnh đáy.

Trả lời:

a) Vẽ đồ thị:

- Đường thẳng $y=2x\left(1\right)$ đi qua gốc tọa độ O và điểm $C\left(1;2\right)$

- Đường thẳng $y=0,5x\left(2\right)$  đi qua gốc tọa độ O và điểm $D\left(1;0,5\right)$

- Đường thẳng $y=-x+6(3)$ đi qua hai điểm : $E\left(0;6\right)$ và điểm $F\left(6;0\right)$

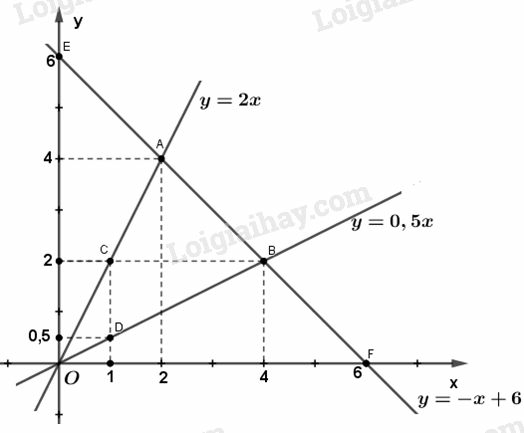
b) Tìm tọa độ của điểm A :

$-x+6=2x\iff x=2$

Thay $x=2$ vào phương trình $y=2x$ ta có $y=2.2=4$

Vậy ta có điểm $A\left(2;4\right)$.

- Tìm tọa độ của điểm B :

$-x+6=0,5x\iff x=4$

Thay $x=4$ vào phương trình $y=0,5x$ ta có :

$y=0,5.4=2$

Vậy ta có điểm $B\left(4;2\right)$ 

c) Chứng minh: $OA=OB$

$OA=\sqrt{4^2+2^2}=\sqrt{20}$ ; $OB=\sqrt{4^2+2^2}=\sqrt{20}$

Vậy $OA=OB\Rightarrow \mathrm{\Delta }OAB$ là tam giác cân $\Rightarrow \widehat{OAB}=\widehat{OBA}$

Tính góc $\widehat{AOF}$ : $\tan \widehat{AOF}=2\Rightarrow \widehat{AOF}\approx {63}^o{26}^{\prime }$

Tính góc $\widehat{BOF}$ : $\tan \widehat{BOF}=0,5\Rightarrow \widehat{BOF}\approx {26}^o{34}^{\prime }$

Vậy $\widehat{AOB}=\widehat{AOF}-\widehat{BOF}$$\approx {63}^o{26}^{\prime }-{26}^o{34}^{\prime }={36}^o{52}^{\prime }$

$\widehat{OAB}=\widehat{OBA}$$\approx {\displaystyle \frac{{180}^o-{36}^o{52}^{\prime }}{2}}={71}^o{34}^{\prime }.$