Với Giải SBT Toán 10 Tập 1 trong Bài tập cuối chương VI Sách bài tập Toán lớp 10 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

SBT Toán 10 Chân trời sáng tạo: Bài tập cuối chương VI

I. TRẮC NGHIỆM

Câu hỏi trang 131 SBT Toán 10

Bài 1 trang 131 SBT Toán 10: Số quy tròn của 45,6534 với độ chính xác $d=0,01$ là:

A. 45,65;

B. 45,6; 

C. 45,7; 

D. 45.

Lời giải:

Hàng lớn nhất của độ chính xác là $d=0,01$ là hàng phần trăm, nên ta quy tròn a đến hàng phần chục ta được số quy tròn của 45,6534 là 45,7

Chọn C.

Bài 2 trang 131 SBT Toán 10: Cho biết $\sqrt[3]{3}=1,\mathrm{44224957...}$Số gần đúng của $\sqrt[3]{3}$ với độ chính xác 0,0001 là:

A. 1,4422;

B.1,4421;   

C. 1,442; 

D. 1,44.

Lời giải:

Hàng lớn nhất của độ chính xác là $d=0,0001$ là hàng phần chục nghìn, nên ta quy tròn a đến hàng phần nghìn ta được số quy tròn của $\sqrt[3]{3}$là 1,4422

Chọn A.

Bài 3 trang 131 SBT Toán 10: Cho số gần đúng $a=0,1571$. Số quy tròn của a với độ chính xác $d=0,002$ là:

A. 0,16;

B. 0,15;

C.0,157;

D. 0,159.

Lời giải:

Hàng lớn nhất của độ chính xác là $d=0,002$ là hàng phần nghìn, nên ta quy tròn a đến hàng phần trăm ta được số quy tròn của $a=0,1571$là 0,16

Chọn A.

Bài 4 trang 131 SBT Toán 10: Độ dài cạnh của một hình vuông là $8\pm 0,2$cm thì chu vi của hình vuông đó bằng:

A. 32 cm ;

B. $32\pm 0,2cm$;

C. $64\pm 0,8cm$;

D. $32\pm 0,8cm$.

Lời giải:

Hình vuông cạnh $a=8\pm 0,2\Rightarrow C=8.4\pm 0,2.4=32\pm 0,8$ cm

Chọn D.

Bài 5 trang 131 SBT Toán 10: Trung vị của mẫu số liệu 4;6;7;6;5;4;5 là:

A. 4; 

B. 5; 

C. 6;   

D. 7.

Lời giải:

Sắp xếp lại theo thứ tự không giảm ta có bảng sau:

Vì $n=7$là số chẵn nên ta có trung vị là : 5

Chọn B.

Bài 6 trang 131 SBT Toán 10: Khoảng biến thiên của mẫu số liệu 6; 7; 9; 4; 7; 5; 6; 6; 7; 9; 5; 6 là:

A. 3; 

B. 4;

C. 5; 

D. 6.

Lời giải:

Sắp xếp số liệu theo thứ tự không giảm, ta được:

Số cao nhất và thấp nhất lần lượt là 9 và 4 do đó khoảng biến thiên của dãy số liệu trên là: $R=9-4=5$

Chọn C.

Bài 7 trang 131 SBT Toán 10: Tứ phân vị thứ nhất của mẫu số liệu 2; 4; 5; 6; 6; 7; 3; 4 là:

A. 3;   

B. 3,5 ; 

C. 4; 

D. 4,5.

Lời giải:

+ Sắp xếp số liệu theo thứ tự không giảm

+ Tứ phân vị: $Q_2=\left(4+5\right):2=4,5$; $Q_1=\left(3+4\right):2=3,5;Q_3=\left(6+6\right):2=6$

Chọn B.

Bài 8 trang 131 SBT Toán 10: Khoảng tứ phân vị của mẫu số liệu 4; 7; 5; 6; 6; 7; 9; 5; 6 là:

A. 1; 

B. 1,5; 

C. 2; 

D. 2,5.

Lời giải:

+ Sắp xếp số liệu theo thứ tự không giảm

+ Tứ phân vị: $Q_2=6$; $Q_1=\left(5+5\right):2=5;Q_3=\left(7+7\right):2=7\Rightarrow \mathrm{\Delta }Q=Q_3-Q_1=2$

Chọn C.

Bài 9 trang 131 SBT Toán 10: Dãy số liệu 5; 6; 0; 3; 5; 10; 3; 4 có các giá trị ngoại lệ là:

A.0;

B. 10;   

C. 0;10;

D. $\mathrm{\varnothing }$.

Lời giải:

+ Sắp xếp số liệu theo thứ tự không giảm

+ Tứ phân vị: $Q_2=\left(4+5\right):2=4,5$; $Q_1=\left(3+3\right):2=3;Q_3=\left(5+6\right):2=5,5\Rightarrow \mathrm{\Delta }Q=Q_3-Q_1=2,5$

Ta có $Q_1-1,5.{\mathrm{\Delta }}_Q=3-1,5.2,5=-0,75$ và $Q_3+1,5.{\mathrm{\Delta }}_Q=5,5+1,5.2,5=9,25$ nên mẫu có giá trị ngoại lệ là 10.

Chọn B.

Bài 10 trang 131 SBT Toán 10: Phương sai của dãy số liệu 4; 5; 0; 3; 3; 5; 6; 10 là:

A. 6,5;

B. 6,75;

C. 7;     

D. 7,25.

Lời giải:

+ Trung bình của mẫu số liệu là $\overline{x}=4,5$

+ Phương sai: $S^2=7,25$

Chọn D.

II. TỰ LUẬN

Bài 1 trang 131 SBT Toán 10: Viết số quy tròn của mỗi số sau với độ chính xác d:

a) $a=-0,4356217$ với $d=0,0001$;

b) $b=0,2042$ với $d=0,001$.

Lời giải:

a) Hàng lớn nhất của độ chính xác là $d=0,0001$ là hàng phần chục nghìn, nên ta quy tròn a đến hàng phần nghìn ta được số quy tròn của $a=-0,4356217$là -0,436

b) Hàng lớn nhất của độ chính xác là $d=0,001$ là hàng phần nghìn, nên ta quy tròn b đến hàng phần trăm ta được số quy tròn của $b=0,2042$ là 0,20

Bài 2 trang 131 SBT Toán 10: Tuấn đo được bán kính của một hình tròn là $5\pm 0,2cm$. Tuấn tính chu vi hình tròn là $p=31,4cm$. Hãy ước lượng sai số tuyệt đối của $p$, biết $3,14<\pi <3,142$. 

Lời giải:

Gọi $\overline{a}$ và $\overline{p}$ lần lượt là bán kính và chu vi hình tròn

Ta có $4,8\le \overline{a}\le 5,2$

Nên $2.3,141.4,8=30,1536\le \overline{p}=2\pi \overline{a}\le 2.3,142.5,2=32,6768$

Do đó $30,1536-31,4=-0,2464\le \overline{p}-31,4\le 32,6768-31,4=1,2768$

Vậy sai số tuyệt đối của $p$ là ${\mathrm{\Delta }}_p=\left|p-31,1\right|\le 1,2768$

Câu hỏi trang 132 SBT Toán 10

Bài 3 trang 132 SBT Toán 10: Bảng sau ghi lại số sách mà các bạn học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường.

a)     Sử dụng số trung bình và trung vị, hãy so sánh số sách mà mỗi học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường.

b)    Hãy xác định giá trị ngoại lệ (nếu có) cho mỗi mẫu số liệu. So sánh số sách mà mỗi học sinh tổ 1 và tổ 2 quyên góp được cho thư viện trường sau khi bỏ đi các giá trị ngoại lệ.

Lời giải:

a)

- Tổ 1:

+ Trung bình của mẫu số liệu là $\overline{x}=7,08$

+ Số trung vị:

Sắp xếp lại theo thứ tự không giảm ta có bảng sau:

Vì $n=12$là số chẵn nên số trung vị của số sách mà mỗi học sinh tổ 1 quyên góp là: $\left(7+7\right):2=7$

- Tổ 2:

+ Trung bình của mẫu số liệu là $\overline{x}=9,58$

+ Số trung vị:

Sắp xếp lại theo thứ tự không giảm ta có bảng sau:

Vì $n=12$là số chẵn nên số trung vị của số sách mà mỗi học sinh tổ 2 quyên góp là: $\left(8+8\right):2=8$

So sánh cả theo số trung bình và trung vị thì số sách các bạn tổ 2 quyên góp nhiều hơn các bạn tổ 1

b)

- Tổ 1:

+ Tứ phân vị: $Q_2=7$; $Q_1=\left(6+6\right):2=6;Q_3=\left(9+9\right):2=9\Rightarrow \mathrm{\Delta }Q=Q_3-Q_1=3$

+ Ta có $Q_1-1,5.{\mathrm{\Delta }}_Q=6-1,5.3=1,5$ và $Q_3+1,5.{\mathrm{\Delta }}_Q=9+1,5.3=13,5$ nên mẫu có giá trị ngoại lệ là 1

+ Bỏ giá trị này, ta có:

Khi đó $\overline{x}=7,64$ và $Me=7$

- Tổ 2:

+ Tứ phân vị: $Q_2=8$; $Q_1=\left(7+7\right):2=7;Q_3=\left(9+9\right):2=9\Rightarrow \mathrm{\Delta }Q=Q_3-Q_1=2$

+ Ta có $Q_1-1,5.{\mathrm{\Delta }}_Q=7-1,5.2=4$ và $Q_3+1,5.{\mathrm{\Delta }}_Q=9+1,5.2=12$ nên mẫu có giá trị ngoại lệ là 30

+ Bỏ giá trị này, ta có:

Khi đó $\overline{x}=7,73$ và $Me=8$

Vậy sau khi bỏ đi các giá trị ngoại lệ thì khi so sánh theo số trung bình và trung vị thì các bạn tổ 2 vẫn quyên góp được nhiều sách hơn các bạn tổ 1

Bài 4 trang 132 SBT Toán 10: Giá bán lúc 10h sáng của một mã cổ phiếu A trong 10 ngày liên tiếp được ghi lại ở biểu đồ sau (đơn vị: nghìn đồng).

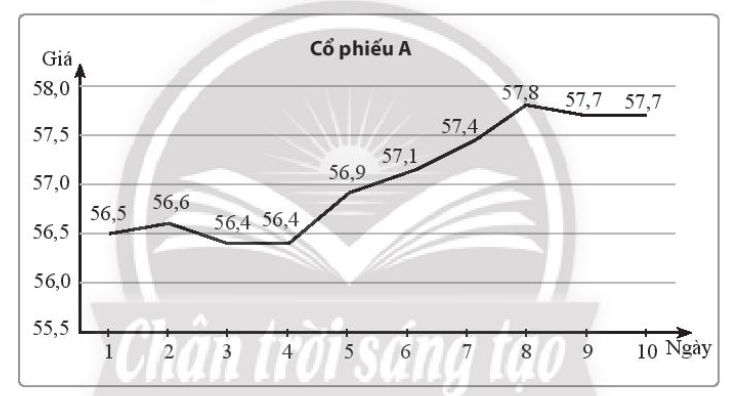
a) Viết mẫu số liệu thống kê giá của mã cổ phiếu A từ biểu đồ trên.

b) Tìm khoảng biến thiện, khoảng tứ phân vị của mẫu số liệu đó.

c) Tính trung bình, độ lệch chuẩn của mẫu số liệu trên.

Lời giải:

a) Bảng thống kê

b)

+ Số cao nhất và thấp nhất lần lượt là 57,8 và 56,4 do đó khoảng biến thiên của dãy số liệu trên là: $R=57,8-56,4=1,4$

+ Tứ phân vị: $Q_2=\left(56,9+57,1\right)=57$; $Q_1=56,5;Q_3=57,7$

c)

+ Trung bình của mẫu số liệu là $\overline{x}=57,05$

+ Phương sai: $S^2=0,2916$

+ Độ lệch chuẩn: $S=\sqrt{S^2}=0,54$

Bài 5 trang 132 SBT Toán 10: Tổng số giờ nắng trong các năm từ 2014 đến 2019 tại hai trạm quan trắc đặt tại Vũng Tàu và Cà Mau được ghi lại ở bảng sau:

a) Sử dụng số trung bình, hãy so sánh số giờ nắng mỗi năm của Vũng Tàu và Cà Mau trong 6 năm trên.

b) Sử dụng số trung vị, hãy so sánh số giờ nắng mỗi năm của Vũng Tàu và Cà Mau trong 6 năm trên.

Lời giải:

a) Số trung bình

+ Vũng Tàu: $\overline{x_1}=\frac{2693,8+2937,8+2690,3+2582,5+2593,9+2814,0}{6}=2718,7$

+ Cà Mau: $\overline{x_2}=\frac{2195,8+2373,4+2104,6+1947,0+1963,7+2063,9}{6}=2108,1$

Nếu sử dụng số trung bình thì thời gian nắng mỗi năm ở Vũng Tàu nhiều hơn ở Cà Mau

b) Sắp xếp lại theo thứ tự không giảm ta có bảng sau:

+ Số trung vị của thời gian nắng mỗi năm ở Vũng Tàu là: $\left(2690,3+2693,8\right):2=2692,05$

+ Số trung vị của thời gian nắng mỗi năm ở Cà Mau là: $\left(2063,9+2104,6\right):2=2084,25$

Nếu sử dụng số trung vị thì thời gian nắng mỗi năm ở Vũng Tàu nhiều hơn ở Cà Mau