Với Giải SBT Toán 10 Tập 2 trong Bài 3: Phương trình quy về phương trình bậc hai Sách bài tập Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10.

SBT Toán 10 Chân trời sáng tạo Bài 3: Phương trình quy về phương trình bậc hai

Câu hỏi trang 18 SBT Toán 10

Bài 1 trang 18 SBT Toán 10: Giải các phương trình sau:

a) $\sqrt{4x^2+15x-19}=\sqrt{5x^2+23x-14}$    

b) $\sqrt{8x^2+10x-3}=\sqrt{29x^2-7x-1}$

c) $\sqrt{-4x^2-5x+8}=\sqrt{2x^2+2x-2}$

d) $\sqrt{5x^2+25x+13}=\sqrt{20x^2-9x+28}$

e) $\sqrt{-x^2-2x+7}=\sqrt{-x-13}$

Lời giải:

a) Bình phương 2 vế của phương trình đã cho, ta được:

                $\begin{array}{l}4x^2+15x-19=5x^2+23x-14\\ \Rightarrow x^2+8x+5=0\end{array}$

                $\Rightarrow x=-4-\sqrt{11}$ hoặc $x=-4+\sqrt{11}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy chỉ có $x=-4-\sqrt{11}$ thỏa mãn

Vậy nghiệm của phương trình là $x=-4-\sqrt{11}$

b) Bình phương 2 vế của phương trình đã cho, ta được:

                $\begin{array}{l}8x^2+10x-3=29x^2-7x-1\\ \Rightarrow 21x^2-17x+2=0\end{array}$

                $\Rightarrow x=\frac{1}{7}$ hoặc $x=\frac{2}{3}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy chỉ có $x=\frac{2}{3}$ thỏa mãn

Vậy nghiệm của phương trình là $x=\frac{2}{3}$

c) Bình phương 2 vế của phương trình đã cho, ta được:

                $\begin{array}{l}-4x^2-5x+8=2x^2+2x-2\\ \Rightarrow 6x^2+7x-10=0\end{array}$

                $\Rightarrow x=-2$ hoặc $x=\frac{5}{6}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai nghiệm đều thỏa mãn

Vậy nghiệm của phương trình là $x=-2$ và $x=\frac{5}{6}$

d) Bình phương 2 vế của phương trình đã cho, ta được:

                $\begin{array}{l}5x^2+25x+13=20x^2-9x+28\\ \Rightarrow 15x^2-34x+15=0\end{array}$

                $\Rightarrow x=\frac{3}{5}$ hoặc $x=\frac{5}{3}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai nghiệm đều thỏa mãn

Vậy nghiệm của phương trình là $x=\frac{3}{5}$ và $x=\frac{5}{3}$

e) Bình phương 2 vế của phương trình đã cho, ta được:

                $\begin{array}{l}-x^2-2x+7=-x-13\\ \Rightarrow x^2+x-20=0\end{array}$

                $\Rightarrow x=-5$ hoặc $x=4$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm

Bài 2 trang 18 SBT Toán 10: Giải các phương trình sau:

a) $2\sqrt{x^2+4x-7}=\sqrt{-4x^2+38x-43}$

b) $\sqrt{6x^2+7x-1}-\sqrt{-29x^2-41x+10}=0$

Lời giải:

a) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}4\left(x^2+4x-7\right)=-4x^2+38x-43\\ \Rightarrow 8x^2-22x+15=0\end{array}$

         $\Rightarrow x=\frac{3}{2}$ _hoặc $x=\frac{5}{4}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy chỉ có $x=\frac{3}{2}$ thỏa mãn

Vậy nghiệm của phương trình là $x=\frac{3}{2}$

_{b) Chuyển các dấu căn về hai vế khác nhau, bình phương hai vế ta được:}

         $\begin{array}{l}\sqrt{6x^2+7x-1}-\sqrt{-29x^2-41x+10}=0\\ \Rightarrow \sqrt{6x^2+7x-1}=\sqrt{-29x^2-41x+10}\\ \Rightarrow 6x^2+7x-1=-29x^2-41x+10\\ \Rightarrow 35x^2+48x-11=0\end{array}$

         $\Rightarrow x=-\frac{11}{7}$ _hoặc $x=\frac{1}{5}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy hai giá trị đều thỏa mãn

Vậy nghiệm của phương trình là $x=-\frac{11}{7}$ _và $x=\frac{1}{5}$

Bài 3 trang 18 SBT Toán 10: Giải các phương trình sau:

a) $\sqrt{-x^2+7x+13}=5$   

b) $\sqrt{-x^2+3x+7}=3$

c) $\sqrt{69x^2-52x+4}=-6x+4$

d) $\sqrt{-x^2-4x+22}=-2x+5$

e) $\sqrt{4x+30}=2x+3$

g) $\sqrt{-57x+139}=3x-11$

Lời giải:

a) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}-x^2+7x+13=25\\ \Rightarrow -x^2+7x-12=0\end{array}$

         $\Rightarrow x=3$ _hoặc $x=4$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn

Vậy nghiệm của phương trình là $x=3$ _và $x=4$

b) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}-x^2+3x+7=9\\ \Rightarrow -x^2+3x-2=0\end{array}$

         $\Rightarrow x=1$ _hoặc $x=2$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn

Vậy nghiệm của phương trình là $x=1$ _hoặc $x=2$

c) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}69x^2-52x+4=36x^2-48x+16\\ \Rightarrow 33x^2-4x-12=0\end{array}$

         $\Rightarrow x=-\frac{6}{11}$ _hoặc $x=\frac{2}{3}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai nghiệm đều thỏa mãn

Vậy nghiệm của phương trình là $x=-\frac{6}{11}$ _hoặc $x=\frac{2}{3}$

d) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}-x^2-4x+22=4x^2-20x+25\\ \Rightarrow 5x^2-16x+3=0\end{array}$

         $\Rightarrow x=3$ _hoặc $x=\frac{1}{5}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy chỉ có $x=\frac{1}{5}$  thỏa mãn

Vậy nghiệm của phương trình là $x=\frac{1}{5}$

e) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}4x+30=4x^2+12x+9\\ \Rightarrow 4x^2+8x-21=0\end{array}$

         $\Rightarrow x=-\frac{7}{2}$ _hoặc $x=\frac{3}{2}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy chỉ có $x=\frac{3}{2}$  thỏa mãn

Vậy nghiệm của phương trình là $x=\frac{3}{2}$

g) Bình phương 2 vế của phương trình đã cho, ta được:

          $\begin{array}{l}-57x+139=9x^2-66x+121\\ \Rightarrow 9x^2-9x-18=0\end{array}$

         $\Rightarrow x=-1$ _hoặc $x=2$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy không có giá trị nào thỏa mãn

Vậy phương trình đã cho vô nghiệm

Bài 4 trang 18 SBT Toán 10: Giải các phương trình sau:

a) $\sqrt{-7x^2-60x+27}+3\left(x-1\right)=0$     

b) $\sqrt{3x^2-9x-5}+2x=5$

c) $\sqrt{-2x+8}-x+6=x$

Lời giải:

a) _Xét phương trình:

          $\begin{array}{l}\sqrt{-7x^2-60x+27}+3\left(x-1\right)=0\\ \iff \sqrt{-7x^2-60x+27}=-3\left(x-1\right)\\ \Rightarrow -7x^2-60x+27=9x^2-18x+9\\ \Rightarrow 16x^2+42x-18=0\end{array}$

         $\Rightarrow x=-3$ _hoặc $x=\frac{3}{8}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn

Vậy nghiệm của phương trình là $x=-3$ _và$x=\frac{3}{8}$

_{b) Xét} phương trình:

          $\begin{array}{l}\sqrt{3x^2-9x-5}+2x=5\\ \iff \sqrt{3x^2-9x-5}=5-2x\\ \Rightarrow 3x^2-9x-5=4x^2-20x+25\\ \Rightarrow x^2-11x+30=0\end{array}$

         $\Rightarrow x=5$ _hoặc $x=6$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta thấy không có giá trị nào thỏa mãn

Vậy phương trình đã cho vô nghiệm

_{c) Xét} phương trình:

          $\begin{array}{l}\sqrt{-2x+8}-x+6=x\\ \iff \sqrt{-2x+8}=2x-6\\ \Rightarrow -2x+8=4x^2-24x+36\\ \Rightarrow 4x^2-22x+28=0\end{array}$

         $\Rightarrow x=2$ _hoặc $x=\frac{7}{2}$

Thay lần lượt các giá trị vừa tìm được vào phương trình ban đầu ta chỉ có $x=\frac{7}{2}$ thỏa mãn

Vậy phương trình đã cho có nghiệm duy nhất là $x=\frac{7}{2}$

Bài 5 trang 19 SBT Toán 10: Khoảng cách từ nhà An ở vị trí N đến cột điện C là 10 m. Từ nhà, An đi x mét theo phương tạo với NC một góc ${60}^{\circ }$ đến vị trí A sau đó đi tiếp 3 m đến vị trí B như hình 1.

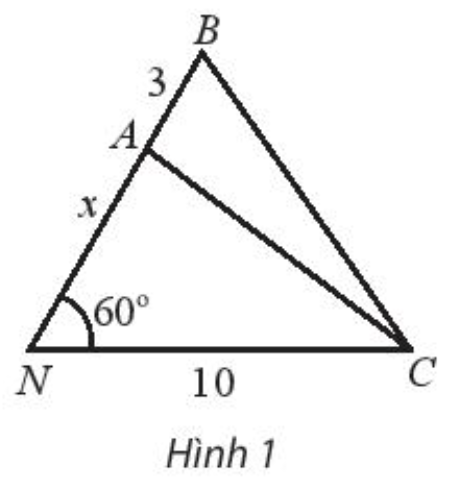
a)  Biểu diễn khoảng cách AC và BC theo x 

b) Tìm x để $AC=\frac{8}{9}BC$

c) Tìm x để khoảng cách $BC=2AN$

Lời giải:

a) Áp dụng đính lí côsin trong tam giác ANC ta có:

$\begin{array}{l}AC=\sqrt{A{N}^2+N{C}^2-2AN.NC.\cos \hat{N}}=\sqrt{x^2+{10}^2-2x.10.\cos {60}^{\circ }}\\ =\sqrt{x^2-10x+100}\end{array}$

Áp dụng đính lí côsin trong tam giác BNC ta có:

$\begin{array}{l}BC=\sqrt{B{N}^2+N{C}^2-2BN.NC.\cos \hat{N}}=\sqrt{{\left(x+3\right)}^2+{10}^2-2\left(x+3\right).10.\cos {60}^{\circ }}\\ =\sqrt{x^2-4x+79}\end{array}$

_{b) Ta có:} $AC=\frac{8}{9}BC$ _hay

$\begin{array}{l}\sqrt{x^2-10x+100}=\frac{8}{9}\sqrt{x^2-4x+79}\\ \Rightarrow x^2-10x+100=\frac{64}{81}\left(x^2-4x+79\right)\\ \Rightarrow \frac{17}{81}{x}^2-\frac{554}{81}x+\frac{3044}{81}=0\end{array}$

$\Rightarrow x\simeq 7$ _hoặc $x\simeq 25,6$

Thay hai giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn

_{Vậy khi} $x\simeq 7$ _hoặc $x\simeq 25,6$ _thì $AC=\frac{8}{9}BC$

c) Yêu cầu bài toán tương đương

$\begin{array}{l}\sqrt{x^2-4x+79}=2x\\ \Rightarrow x^2-4x+79=4x^2\\ \Rightarrow 3x^2+4x-79=0\end{array}$

$\Rightarrow x=\frac{-2-\sqrt{241}}{3}$ _hoặc $x=\frac{-2+\sqrt{241}}{3}$

_{Mà vì} $x\ge 0$ _nên  $x=\frac{-2+\sqrt{241}}{3}$

_{Vậy khi} $x=\frac{-2+\sqrt{241}}{3}$ _thì $BC=2AN$