Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 3. Phương trình quy về phương trình bậc hai sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 2. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo Bài 3: Phương trình quy về phương trình bậc hai

1. Phương trình dạng $\sqrt{a{x}^2+bx+c}= \sqrt{d{x}^2+ex+f}$

Câu hỏi trang 15 Toán 10

HĐ Khởi động trang 15 Toán 10 Tập 2: Trong hình bên, các tam giác vuông được xếp với nhau để tạo thành một

Phương pháp giải:

Bước 1: Bình phương hai vế làm mất căn bậc hai

Bước 2: Rút gọn và giải phương trình vừa tìm được

Bước 3: Thử lại nghiệm vừa tìm được và kết luận

Lời giải 

Ta có điều kiện hiểu nhiên $x>0$

$\begin{array}{l}\sqrt{x^2-1}=\frac{1}{2}\sqrt{x^2+1}\\ \Rightarrow x^2-1=\frac{1}{4}\left(x^2+1\right)\\ \Rightarrow \frac{3}{4}{x}^2-\frac{5}{4}=0\end{array}$

$\Rightarrow x=\pm \sqrt{\frac{5}{3}}$

Thử lại, kết hợp điều kiện của x ta thấy $x=\sqrt{\frac{5}{3}}$ thỏa mãn phương trình.

Vậy khi $x=\sqrt{\frac{5}{3}}$ thì $OA=\frac{1}{2}OC$

HĐ Khám phá 1 trang 15 Toán 10 Tập 2: Lời giải cho phương trình $\sqrt{-2x^2-2x+11}=\sqrt{-x^2+3}$ như sau đúng hai sai?

$$$\sqrt{-2x^2-2x+11}=\sqrt{-x^2+3}$           

$\Rightarrow -2x^2-2x+11=-x^2+3$ (bình phương cả hai vế để làm mất dấu căn)

$\Rightarrow x^2+2x-8=0$  (chuyển vế, rút gọn)

$\Rightarrow x=2$ hoặc $x=-4$  (giải phương trình bậc hai)

Vậy phương trình đã cho có hai nghiệm là 2 và -4

Lời giải 

Thay $x=2$ vào phương trình $\sqrt{-2x^2-2x+11}=\sqrt{-x^2+3}$ ta thấy không thỏa mãn vì dưới dấu căn là $-1$ không thỏa mãn

Vậy $x=2$ không là nghiệm của phương trình do đó lời giải như trên là sai.

Câu hỏi trang 16 Toán 10

Thực hành 1 trang 16 Toán 10 Tập 2: Giải phương trình $\sqrt{31x^2-58x+1}=\sqrt{10x^2-11x-19}$

Phương pháp giải:

Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 3: Giải phương trình nhận được ở bước 2

Bước 4: Thử lại xem nghiệm đã tìm được ở bước 3 có thỏa mãn phương trình không và kết luận

Lời giải 

Bình phương hai vế của phương trình đã cho, ta được:

$\begin{array}{l}\sqrt{31x^2-58x+1}=\sqrt{10x^2-11x-19}\\ \Rightarrow 31x^2-58x+1=10x^2-11x-19\\ \Rightarrow 21x^2-47x+20=0\end{array}$

$\Rightarrow x=\frac{5}{3}$ hoặc $x=\frac{4}{7}$

Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn

Vậy phương trình đã cho vô nghiệm

Chú ý khi giải: sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau).

2. Phương trình dạng $\sqrt{a{x}^2+bx+c}= dx+e$

HĐ Khám phá 2 trang 16 Toán 10 Tập 2: Lời giải cho phương trình $\sqrt{-x^2+x+1}=x$ như sau đúng hai sai?

$$$\sqrt{-x^2+x+1}=x$               

$\Rightarrow -x^2+x+1=x^2$  (bình phương cả hai vế để làm mất dấu căn)

$\Rightarrow -2x^2+x+1=0$   (chuyển vế, rút gọn)

$\Rightarrow x=1$ hoặc $x=-\frac{1}{2}$ (giải phương trình bậc hai)

Vậy phương trình đã cho có hai nghiệm là 1 và $-\frac{1}{2}$

Phương pháp giải:

Thay nghiệm tìm được vào phương trình ban đầu ta có:

+) Thay $x=1$ vào phương trình $\sqrt{-x^2+x+1}=x$ ta thấy thảo mãn phương trình

+) Thay $x=-\frac{1}{2}$ vào $\sqrt{-x^2+x+1}=x$ ta thấy không thỏa mãn phương trình

Vậy nghiệm của phương trình là $x=1$, suy ra lời giải như trên là sai.

Thực hành 2 trang 16 Toán 10 Tập 2: Giải phương trình $\sqrt{3x^2+27x-41}=2x+3$

Phương pháp giải:

Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 3: Giải phương trình nhận được ở bước 2

Bước 4: Thử lại và kết luận

Lời giải 

Bình phương hai vế của phương trình đã cho, ta được:

$3x^2+27x-41={\left(2x+3\right)}^2$

$\Rightarrow 3x^2+27x-41=4x^2+12x+9$

$\Rightarrow x^2-15x+50=0$

$\Rightarrow x=5$ và $x=10$

Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{3x^2+27x-41}=2x+3$ ta thấy cả hai nghiệm đều thỏa mãn phương trình

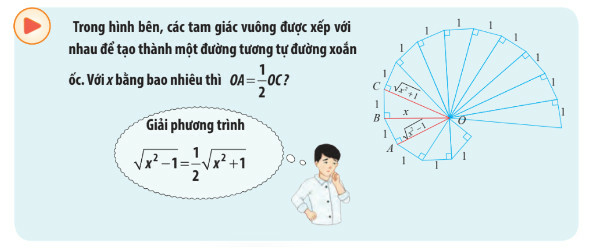
Vậy nghiệm của phương trình đã cho là $x=5$ và $x=10$.

Câu hỏi trang 17 Toán 10

Vận dụng trang 17 Toán 10 Tập 2: Cho tam giác OAB và OBC lần lượt vuông tại A và B như hình 1. Các cạnh AB và BC bằng nhau và ngắn hơn OB là 1 cm. Hãy biểu diễn độ dài OC và OA qua OB, từ đó xác định OB để:

a) $OC=3OA;$

b) $OC=\frac{5}{4}OB$

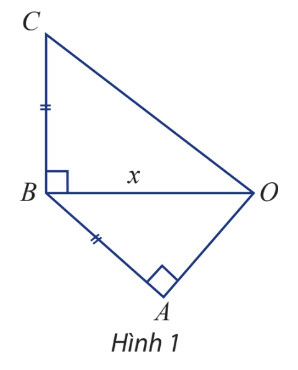
Phương pháp giải:

Bước 1: Sử dụng giả thiết và áp dụng định lý pitago để biểu diễn độ dài OC và OA qua OB

Bước 2: Lập phương trình theo giả thiết $OC=3OA;$$OC=\frac{5}{4}OB$

Bước 3: Giải phương trình

Lời giải 

Gọi độ dài cạnh OB là x cm $\left(x>0\right)$

Theo giả thiết ta có $AB=BC=OB-1=x-1$

Áp dụng định lý pitago trong tam giác vuông OAB và OBC ta có:

$OC=\sqrt{O{B}^2+B{C}^2}=\sqrt{x^2+{\left(x-1\right)}^2}=\sqrt{2x^2-2x+1}$

$OA=\sqrt{O{B}^2-A{B}^2}=\sqrt{x^2-{\left(x-1\right)}^2}=\sqrt{2x-1}$

a) $OC=3OA\Rightarrow \sqrt{2x^2-2x+1}=3\sqrt{2x-1}$

$\begin{array}{l}\Rightarrow 2x^2-2x+1=9\left(2x-1\right)\\ \Rightarrow 2x^2-20x+10=0\end{array}$

$\Rightarrow$$x=5-2\sqrt{5}$ và $x=5+2\sqrt{5}$

Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{2x^2-2x+1}=3\sqrt{2x-1}$ ta thấy cả hai đều thỏa mãn phương trình

Vậy khi $OB=5-2\sqrt{5}$ hoặc $OB=5+2\sqrt{5}$thì $OC=3OA$

b) $OC=\frac{5}{4}OB\Rightarrow \sqrt{2x^2-2x+1}=\frac{5}{4}x$

$\begin{array}{l}\Rightarrow 2x^2-2x+1=\frac{25}{16}{x}^2\\ \Rightarrow \frac{7}{16}{x}^2-2x+1=0\end{array}$$$

$\Rightarrow x=\frac{4}{7}$ hoặc $x=4$                

Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{2x^2-2x+1}=\frac{5}{4}x$ ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy khi $OB=\frac{4}{7}$ hoặc $OB=4$ (cm) thì  $OC=\frac{5}{4}OB$.

Bài tập 

Bài 1 trang 17 Toán 10 Tập 2: Giải các phương trình sau:

a) $\sqrt{11x^2-14x-12}=\sqrt{3x^2+4x-7}$

b) $\sqrt{x^2+x-42}=\sqrt{2x-30}$

c) $2\sqrt{x^2-x-1}=\sqrt{x^2+2x+5}$

d) $3\sqrt{x^2+x-1}-\sqrt{7x^2+2x-5}=0$

Phương pháp giải

Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 3: Giải phương trình nhận được ở bước 2

Bước 4: Thử lại nghiệm và kết luận

Lời giải 

a) $\sqrt{11x^2-14x-12}=\sqrt{3x^2+4x-7}$

$\begin{array}{l}\Rightarrow 11x^2-14x-12=3x^2+4x-7\\ \Rightarrow 8x^2-18x-5=0\end{array}$

$\Rightarrow x=-\frac{1}{4}$ và $x=\frac{5}{2}$

Thay nghiệm vừa tìm được vào phương trình $\sqrt{11x^2-14x-12}=\sqrt{3x^2+4x-7}$ ta thấy chỉ có nghiệm $x=\frac{5}{2}$ thảo mãn phương trình

Vậy nhiệm của phương trình đã cho là $x=\frac{5}{2}$

b) $\sqrt{x^2+x-42}=\sqrt{2x-30}$

$\begin{array}{l}\Rightarrow x^2+x-42=2x-3\\ \Rightarrow x^2-x-12=0\end{array}$

$\Rightarrow x=-3$ và $x=4$

Thay vào phương trình $\sqrt{x^2+x-42}=\sqrt{2x-30}$  ta thấy  không có nghiệm nào thỏa mãn

Vậy phương trình đã cho vô nghiệm

c) $2\sqrt{x^2-x-1}=\sqrt{x^2+2x+5}$

$\begin{array}{l}\Rightarrow 4.\left(x^2-x-1\right)=x^2+2x+5\\ \Rightarrow 3x^2-6x-9=0\end{array}$

$\Rightarrow x=-1$ và $x=3$

Thay hai nghiệm trên vào phương trình $2\sqrt{x^2-x-1}=\sqrt{x^2+2x+5}$ ta thấy cả hai nghiệm đếu thỏa mãn phương trình

Vậy nghiệm của phương trình $2\sqrt{x^2-x-1}=\sqrt{x^2+2x+5}$ là $x=-1$ và $x=3$

d) $3\sqrt{x^2+x-1}-\sqrt{7x^2+2x-5}=0$

$\begin{array}{l}\Rightarrow 3\sqrt{x^2+x-1}=\sqrt{7x^2+2x-5}\\ \Rightarrow 9.\left(x^2+x-1\right)=7x^2+2x-5\\ \Rightarrow 2x^2+7x-4=0\end{array}$

$\Rightarrow x=-4$ và $x=\frac{1}{2}$

Thay hai nghiệm trên vào phương trình $3\sqrt{x^2+x-1}-\sqrt{7x^2+2x-5}=0$ ta thấy chỉ có nghiệm $x=-4$ thỏa mãn phương trình

Vậy nghiệm của phương trình trên là $x=-4$.

Bài 2 trang 17 Toán 10 Tập 2: Giải các phương trình sau:

a) $\sqrt{x^2+3x+1}=3$

b) $\sqrt{x^2-x-4}=x+2$

c) $2+\sqrt{12-2x}=x$

d) $\sqrt{2x^2-3x-10}=-5$

Phương pháp giải 

Bước 1: Chuyển biểu thức có căn về một vế

Bước 2: Bình phương hai vế của phương trình để làm mất dấu căn

Bước 3: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn

Bước 4: Giải phương trình nhận được ở bước 2

Bước 5: Thử lại nghiệm và kết luận

Lời giải 

a) $\sqrt{x^2+3x+1}=3$

$\begin{array}{l}\Rightarrow x^2+3x+1=9\\ \Rightarrow x^2+3x-8=0\end{array}$

$\Rightarrow x=\frac{-3-\sqrt{41}}{2}$ và $x=\frac{-3+\sqrt{41}}{2}$

Thay hai nghiệm trên vào phương trình $\sqrt{x^2+3x+1}=3$ ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy nghiệm của phương trình đã cho là $x=\frac{-3-\sqrt{41}}{2}$ và $x=\frac{-3+\sqrt{41}}{2}$

b) $\sqrt{x^2-x-4}=x+2$

$\begin{array}{l}\Rightarrow x^2-x-4={\left(x+2\right)}^2\\ \Rightarrow x^2-x-4=x^2+4x+4\\ \Rightarrow 5x=-8\\ \Rightarrow x=-\frac{8}{5}\end{array}$

Thay $x=-\frac{8}{5}$ và phương trình $\sqrt{x^2-x-4}=x+2$ ta thấy thỏa mãn phương trình

Vậy nghiệm của phương trình đã cho là $x=-\frac{8}{5}$

c) $2+\sqrt{12-2x}=x$

$\begin{array}{l}\Rightarrow \sqrt{12-2x}=x-2\\ \Rightarrow 12-2x={\left(x-2\right)}^2\\ \Rightarrow 12-2x=x^2-4x+4\\ \Rightarrow x^2-2x-8=0\end{array}$

$\Rightarrow x=-2$ và $x=4$

Thay hai nghiệm vừa tìm được vào phương trình $2+\sqrt{12-2x}=x$ thì thấy chỉ có $x=4$ thỏa mãn

Vậy $x=4$ là nghiệm của phương trình đã cho.

d) Ta có biểu thức căn bậc hai luôn không âm nên $\sqrt{2x^2-3x-10}\ge 0\mathrm{\forall }x\in \mathbb{R}$

$\Rightarrow \sqrt{2x^2-3x-10}=-5$ (vô lí)

Vậy phương trình đã cho vô nghiệm.

Bài 3 trang 17 Toán 10 Tập 2: Cho tam giác ABC vuông tại A có AB ngắn hơn AC là 2 cm.

a) Biểu diễn độ dài cạnh huyền BC theo AB

b) Biết chu vi của tam giác ABC là 24 cm. Tính độ dài ba cạnh của tam giác đó.

Phương pháp giải

a)       Bước 1: Đặt độ dài cạnh AB là x ($x>0$), biểu diễn AC theo AB

          Bước 2: Áp dụng định lý Pitago biểu diễn cạnh BC

b)       Bước 1: Lập biểu thức tính chu vi của tam giác

          Bước 2: Giải phương trình vừa tìm được

Lời giải 

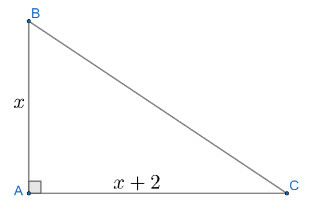
a) Đặt độ dài cạnh AB là x ($x>0$)

Theo giả thiết ta có độ dài $AC=AB+2=x+2$

Áp dụng định lý pitago trong tam giác vuông ta có

$BC=\sqrt{A{B}^2+A{C}^2}=\sqrt{x^2+{\left(x+2\right)}^2}=\sqrt{2x^2+4x+4}$

b) Chu vi của tam giác là $C=AB+AC+BC$

$\Rightarrow C=x+\left(x+2\right)+\sqrt{2x^2+4x+4}=2x+2+\sqrt{2x^2+4x+4}$

Theo giả thiết ta có

$\begin{array}{l}C=24\iff 2x+2+\sqrt{2x^2+4x+4}=24\\ \iff \sqrt{2x^2+4x+4}=22-2x\\ \Rightarrow 2x^2+4x+4={\left(22-2x\right)}^2\\ \Rightarrow 2x^2+4x+4=4x^2-88x+484\\ \Rightarrow 2x^2-92x+480=0\end{array}$

$\Rightarrow x=6$ hoặc $x=40$

Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{2x^2+4x+4}=22-2x$ ta thấy chỉ có  $x=6$ thỏa mãn phương trình

Vậy độ dài ba cạnh của tam giác là $AB=6;AC=8$ và $BC=10$(cm).

Bài 4 trang 17 Toán 10 Tập 2: Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc ${60}^{\circ }$. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng 1km và 2km (Hình 2).

a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.

b) Tìm x để khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A

c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.

Lưu ý: Làm tròn kết quả đến hàng phần trăm. 

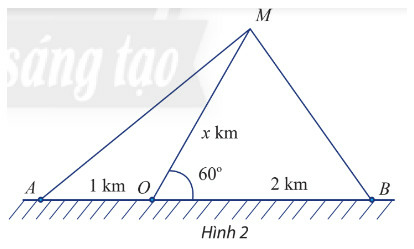
Phương pháp giải

a) Sử dụng định lý cosin $a^2=b^2+c^2+2bc\cos A$

b) Lập phương trình $MB=\frac{4}{5}MA$, và giải phương trình lập được

c) Lập phương trình $MB=MO-0,5$ và giải phương trình lập được

Lời giải 

a) Đặt độ dài của MO là x km $\left(x>0\right)$

Ta có: $\widehat{MOA}+\widehat{MOB}={180}^{\circ }$ (hai góc bù nhau) $\Rightarrow \widehat{MOA}={120}^{\circ }$

Áp dụng định lý Cosin trong tam giác ta tính được:

+) Khoảng cách từ tàu đến B là $MB=\sqrt{x^2+2^2-\mathrm{2.2.}x.\cos {60}^{\circ }}=\sqrt{x^2-2x+4}$

+) Khoảng cách từ tàu đến A là $MA=\sqrt{x^2+1^2-\mathrm{2.1.}x.\cos {120}^{\circ }}=\sqrt{x^2+x+1}$

b) Theo giải thiết ta có phương trình $MB=\frac{4}{5}MA\Rightarrow \sqrt{x^2-2x+4}=\frac{4}{5}\sqrt{x^2+x+1}$

$\begin{array}{l}\Rightarrow x^2-2x+4=\frac{16}{25}\left(x^2+x+1\right)\\ \Rightarrow \frac{9}{25}{x}^2-\frac{66}{25}x+\frac{84}{25}=0\end{array}$

$\Rightarrow x\simeq 1,64$ và $x\simeq 5,69$

Thay hai nghiệm vừa tìm được vào phương trình $\sqrt{x^2-2x+4}=\frac{4}{5}\sqrt{x^2+x+1}$ ta thấy cả hai nghiệm đều thỏa mãn phương trình

Vậy khi  $x\simeq 1,64$ hoặc $x\simeq 5,69$ thì khoảng cách từ tàu đến B bằng $\frac{4}{5}$ khoảng cách từ tàu đến A

c) Đổi 500 m = 0,5 km

Theo giả thiết ta có phương trình sau:

$\begin{array}{l}MB=MO-0,5\Rightarrow \sqrt{x^2-2x+4}=x-0,5\\ \Rightarrow x^2-2x+4={\left(x-0,5\right)}^2\\ \Rightarrow x^2-2x+4=x^2-x+\frac{1}{4}\\ \Rightarrow x=\frac{15}{4}\end{array}$

Thay $x=\frac{15}{4}$ vào phương trình $\sqrt{x^2-2x+4}=x-0,5$ ta thấy thỏa mãn phương trình

Vậy khi $x=\frac{15}{4}$ thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.