Toán 10 Chân trời sáng tạo trang 73 Bài 2: Định lí Cosin và định lí sin

Giang Ngày: 07-02-2023 Lớp 10

400

Với giải Câu hỏi trang 73 Toán 10 Tập 1 Chân trời sáng tạo chi tiết trong Bài 2: Định lí Cosin và định lí sin giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Chân trời sáng tạo trang 73 Bài 2: Định lí Cosin và định lí sin

Bài 4 trang 73 Toán 10 Tập 1: Một công viên có dạng hình tam giác với các kích thước như Hình 15. Tính số đo các góc của tam giác đó.

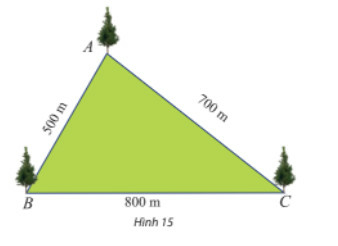
Bài 4 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Áp dụng định lí cosin để tính góc:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b} .$

Lời giải

Đặt $a = B C, b = A C, c = A B$

Ta có: $a = 800, b = 700, c = 500.$

Áp dụng định lí cosin, ta có:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}; \cos B = \frac{a^{2} + c^{2} - b^{2}}{2 a c}; \cos C = \frac{a^{2} + b^{2} - c^{2}}{2 a b} .$

Suy ra:

$\begin{array}{l} \cos A = \frac{700^{2} + 500^{2} - 800^{2}}{2.700.500} = \frac{1}{7} \Rightarrow \hat{A} = 81^{o} 47^{'} 12, 44^{″}; \\ \cos B = \frac{500^{2} + 800^{2} - 700^{2}}{2.500.800} = \frac{1}{2} \Rightarrow \hat{B} = 60^{o}; \\ \cos C = \frac{800^{2} + 700^{2} - 500^{2}}{2.800.700} = \frac{11}{14} \Rightarrow \hat{C} = 38^{o} 12^{'} 47, 56^{″} . \end{array}$

Vậy $\hat{A} = 81^{o} 47^{'} 12, 44^{″}; \hat{B} = 60^{o}; \hat{C} = 38^{o} 12^{'} 47, 56^{″} .$

Bài 5 trang 73 Toán 10 Tập 1: Tính diện tích một lá cờ hình tam giác cân có độ dài cạnh bên là 90 cm và góc ở đỉnh là $35^{o} .$

Bài 5 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Phương pháp giải

Tính diện tích bằng công thức: $S = \frac{1}{2} b c \sin A$

Lời giải

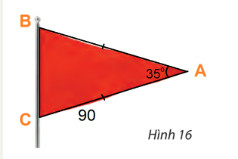
Bài 5 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 2)

Kí hiệu các điểm A, B, C như hình trên.

Từ giả thiết ta có: $A B = A C = 90, \hat{A} = 35^{o}$

Áp dụng công thức $S = \frac{1}{2} b c \sin A$ , ta có: $S = \frac{1}{2} .90 .90 . c \sin 35^{o} \approx 2323 (c m^{2})$

Bài 6 trang 73 Toán 10 Tập 1: Cho tam giác ABC có $A B = 6, A C = 8$ và $\hat{A} = 60^{o} .$

a) Tính diện tích tam giác ABC.

b) Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Tính diện tích tam giác IBC

Phương pháp giải

a) Tính diện tích bằng công thức: $S = \frac{1}{2} b c \sin A$

b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC

Lời giải

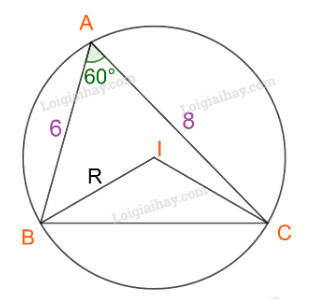
Đặt $a = B C, b = A C, c = A B .$

a) Áp dụng công thức $S = \frac{1}{2} b c \sin A$ , ta có: $S_{A B C} = \frac{1}{2} .8 .6 . \sin 60^{o} = \frac{1}{2} .8 .6 . \frac{\sqrt{3}}{2} = 12 \sqrt{3}$

b) Áp dụng định lí cosin cho tam giác ABC ta được:

$\begin{array}{l} B C^{2} = a^{2} = 8^{2} + 6^{2} - 2.8.6. \cos 60^{o} = 52 \\ \Rightarrow B C = 2 \sqrt{13} \end{array}$

Xét tam giác IBC ta có:

Góc $\hat{B I C} = 2. \hat{B A C} = 120^{o}$ (góc ở tâm và góc nội tiếp cùng chắn một cung)

$I B = I C = R = \frac{a}{\sin A} = \frac{2 \sqrt{13}}{\frac{\sqrt{3}}{2}} = \frac{4 \sqrt{39}}{3} .$

$\Rightarrow S_{I B C} = \frac{1}{2} . \frac{4 \sqrt{39}}{3} . \frac{4 \sqrt{39}}{3} \sin 120^{o} = \frac{52 \sqrt{3}}{3} .$

Bài 7 trang 73 Toán 10 Tập 1: Cho tam giác ABC có trọng tâm G và độ dài ba cạnh AB, BC, CA lần lượt là 15, 18, 27.

a) Tính diện tích và bán kính đường tròn nội tiếp tam giác ABC.

b) Tính diện tích tam giác GBC.

Phương pháp giải

a) Tính r bằng công thức: $S = p . r$ . Trong đó S tính bởi công thức heron.

b) Tìm a, từ đó suy ra R bằng định lí sin => Tính diện tích tam giác IBC

Lời giải

a) Đặt $a = B C, b = A C, c = A B .$

Ta có: $p = \frac{1}{2} (15 + 18 + 27) = 30$

Áp dụng công thức heron, ta có:

$S_{A B C} = \sqrt{30 (30 - 15) (30 - 18) (30 - 27)} = 90 \sqrt{2}$

Và $r = \frac{S}{p} = \frac{90 \sqrt{2}}{30} = 3 \sqrt{2}$

b) Gọi, H, K lần lượt là chân đường cao hạ từ A và G xuống BC, M là trung điểm BC.

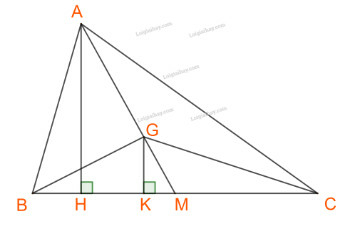
Bài 7 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

G là trọng tâm tam giác ABC nên $G M = \frac{1}{3} A M$

$\begin{array}{l} \Rightarrow G K = \frac{1}{3} . A H \\ \Rightarrow S_{G B C} = \frac{1}{3} . S_{A B C} = \frac{1}{3} .90 \sqrt{2} = 30 \sqrt{2} . \end{array}$

Xét tam giác IBC ta có:

Góc $\hat{B I C} = 2. \hat{B A C} = 120^{o}$ (góc ở tâm và góc nội tiếp cùng chắn một cung)

$I B = I C = R = \frac{a}{\sin A} = \frac{2 \sqrt{13}}{\frac{\sqrt{3}}{2}} = \frac{4 \sqrt{39}}{3} .$

$\Rightarrow S_{I B C} = \frac{1}{2} . \frac{4 \sqrt{39}}{3} . \frac{4 \sqrt{39}}{3} \sin 120^{o} = \frac{52 \sqrt{3}}{3} .$

Bài 8 trang 73 Toán 10 Tập 1: Cho $h_{a}$ là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: $h_{a} = 2 R . \sin B . \sin C$

Phương pháp giải

Bước 1: Tính $h_{a}$ theo b và sinC

Bước 2: Tính b theo R và sinB. Từ đó suy ra điều phải chứng minh. $h_{a} = 2 R \sin B \sin C .$

Lời giải

Đặt $a = B C, b = A C, c = A B$

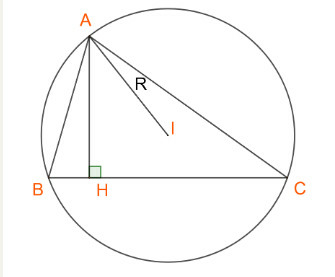
Bài 8 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Ta có: $\sin C = \frac{A H}{A C} = \frac{h_{a}}{b} \Rightarrow h_{a} = b . \sin C$

Theo định lí sin, ta có: $\frac{b}{\sin B} = 2 R \Rightarrow b = 2 R . \sin B$

$\Rightarrow h_{a} = 2 R . \sin B . \sin C$

Bài 9 trang 73 Toán 10 Tập 1: Cho tam giác ABC có góc B nhọn, AD và CE là hai đường cao.

a) Chứng minh $\frac{S_{B D E}}{S_{B A C}} = \frac{B D . B E}{B A . B C} .$

b) Biết rằng $S_{A B C} = 9 S_{B D E}$ và $D E = 2 \sqrt{2} .$ Tính $\cos B$ và bán kính đường tròn ngoại tiếp tam giác ABC.

Phương pháp giải

a) Tính diện tích bằng công thức $S = \frac{1}{2} a c . \sin B$

b) $\cos B = \frac{B D}{B A} = \frac{B E}{B C}$

Lời giải

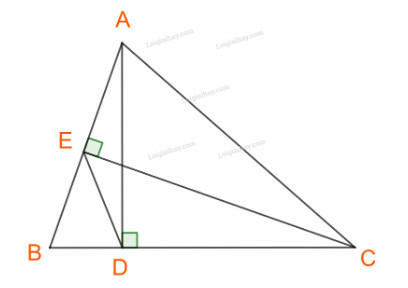
Bài 9 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

a) Áp dụng công thức $S = \frac{1}{2} a c . \sin B$ cho tam giác ABC và BED, ta có:

$S_{A B C} = \frac{1}{2} . B A . B C . \sin B; S_{B E D} = \frac{1}{2} . . B E . B D . \sin B$

$\Rightarrow \frac{S_{B E D}}{S_{A B C}} = \frac{\frac{1}{2} . B E . B D . \sin B}{\frac{1}{2} . B A . B C . \sin B} = \frac{B E . B D}{B A . B C}$

b) Ta có: $\cos B = \frac{B D}{B A} = \frac{B E}{B C}$

Mà $\frac{S_{B E D}}{S_{A B C}} = \frac{1}{9} \Rightarrow \frac{B D}{B A} . \frac{B E}{B C} = \frac{1}{9}$

$\Rightarrow \cos B = \frac{B D}{B A} = \frac{B E}{B C} = \frac{1}{3}$

+) Xét tam giác ABC và tam giác DEB ta có:

$\frac{B E}{B C} = \frac{B D}{B A} = \frac{1}{3}$ và góc B chung

$\Rightarrow Δ A B C \sim Δ D E B$ (cgc)

$\Rightarrow \frac{D E}{A C} = \frac{1}{3} \Rightarrow A C = 3. D E = 3.2 \sqrt{2} = 6 \sqrt{2} .$

Ta có: $\cos B = \frac{1}{3} \Rightarrow \sin B = \sqrt{1 - {(\frac{1}{3})}^{2}} = \frac{2 \sqrt{2}}{3}$ (do B là góc nhọn)

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{A C}{\sin B} = 2 R \Rightarrow R = \frac{6 \sqrt{2}}{\frac{2 \sqrt{2}}{3}} : 2 = \frac{9}{2}$

Bài 10 trang 73 Toán 10 Tập 1: Cho tứ giác lồi ABCD có các đường chéo $A C = x, B D = y$ và góc giữa AC và BD bằng $α .$ Gọi S là diện tích của tứ giác ABCD.

a) Chứng minh $S = \frac{1}{2} x y . \sin α$

b) Nêu kết quả trong trường hợp $A C ⊥ B D .$

Phương pháp giải

a) Tính diện tích 4 tam giác nhỏ theo $\sin α$ .

Chú ý: $\sin (180^{o} - α) = \sin α$

b) $α = 90^{o}$ thì $\sin α = 1$

Lời giải

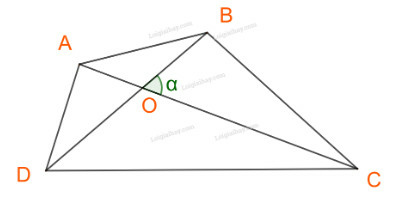
Bài 10 trang 73 Toán 10 Tập 1 Chân trời sáng tạo (ảnh 1)

Gọi O là giao điểm của AC và BD.

a) Áp dụng công thức $S = \frac{1}{2} a c . \sin B$ , ta có:

$\begin{array}{l} S_{O A D} = \frac{1}{2} . O A . O D . \sin α; S_{O B C} = \frac{1}{2} . . O B . O C . \sin α; \\ S_{O A B} = \frac{1}{2} . O A . O B . \sin (180^{o} - α); S_{O C D} = \frac{1}{2} . O D . O C . \sin (180^{o} - α) . \end{array}$

Mà $\sin (180^{o} - α) = \sin α$

$\Rightarrow S_{O A B} = \frac{1}{2} . O A . O B . \sin α; S_{O C D} = \frac{1}{2} . O D . O C . \sin α .$

$\begin{array}{l} \Rightarrow S_{A B C D} = (S_{O A D} + S_{O A B}) + (S_{O B C} + S_{O C D}) \\ = \frac{1}{2} . O A . \sin α . (O D + O B) + \frac{1}{2} . O C . \sin α . (O B + O D) \\ = \frac{1}{2} . O A . \sin α . B D + \frac{1}{2} . O C . \sin α . B D \\ = \frac{1}{2} . B D . \sin α . (O A + O C) \\ = \frac{1}{2} . A C . B D . \sin α = \frac{1}{2} . x . y . \sin α . \end{array}$