Với giải Câu hỏi trang 58 Toán 10 Tập 2 Kết nối tri thức chi tiết trong Bài tập cuối chương 8 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
SBT Toán 10 Kết nối tri thức trang 58: Bài tập cuối chương 8
A. 5.
B. 10.
C. 15.
D. 20.
Lời giải:
Đáp án đúng là: D
Từ Hà Nội tới Hải Phòng, một hành khách có 5 cách chọn nhà xe.
Để quay lại Hà Nội bằng một nhà xe khác thì hành khách có 5 – 1= 4 cách chọn.
Như vậy, theo quy tắc nhân thì số cách đi là 5 . 4 = 20 (cách).
A. 224.
B. 280.
C. 324.
D. Không số nào trong các số đó.
Lời giải:
Đáp án đúng là: A
Một số có ba chữ số như vậy có dạng 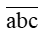
Có 4 cách chọn c là một trong các chữ số 2; 4; 6; 8.
Có 8 cách chọn a (bớt đi 1 số đã chọn bởi c).
Có 7 cách chọn b (bớt đi 1 số đã chọn bởi c, 1 số đã chọn bởi a).
Vì thế, theo quy tắc nhân, số các số có tính chất của bài toán là:
4 . 8 . 7 = 224 (số).
A. .
B. .
C. .
D. .
Lời giải:
Đáp án đúng là: B
Một số tự nhiên nằm trong khoảng từ 3 000 đến 4 000 và chia hết cho 5 và có các chữ số được tạo thành từ các chữ số 1; 2; 3; 4; 5; 6 phải có chữ số hàng đơn vị là 5 và chữ số hàng nghìn là 3. Như vậy các số thoả mãn yêu cầu của bài toán có dạng 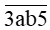
Bài 8.21 trang 58 SBT Toán 10 Tập 2: Cho số nguyên dương n ≥ 4. Người ta đánh dấu n điểm phân biệt trên một đường tròn. Biết rằng số các hình tam giác với các đỉnh là các điểm được đánh dấu thì bằng số các tứ giác với các đỉnh là các điểm được đánh dấu. Giá trị của n là
A. 4.
B. 6.
C. 7.
D. 9.
Lời giải:
Đáp án đúng là: C
Mỗi tam giác cần đếm có 3 đỉnh là các điểm được đánh dấu.
Đảo lại, mỗi bộ ba điểm được đánh dấu xác định một tam giác.
Như vậy, do khi đảo cách thứ tự 3 đỉnh đã chọn cho nhau thì tam giác tạo thành không thay đổi nên số các tam giác với các điểm được đánh dấu là số các tổ hợp chập 3 của n và là: .
Mỗi tứ giác cần đếm có 4 đỉnh là các điểm được đánh dấu.
Đảo lại, mỗi bộ bốn điểm được đánh dấu xác định một tứ giác.
Như vậy, do khi đảo cách thứ tự 4 đỉnh đã chọn cho nhau thì tứ giác tạo thành không thay đổi nên số các tứ giác với các điểm được đánh dấu là số các tổ hợp chập 4 của n và là: .
Biết rằng số các hình tam giác với các đỉnh là các điểm được đánh dấu thì bằng số các tứ giác với các đỉnh là các điểm được đánh dấu. Suy ra , nghĩa là
Mà n ≥ 4 nên chọn n = 7.
A. .
B. 53.
C. 35.
D. Không số nào trong các số đó.
Lời giải:
Đáp án đúng là: C
Mỗi thành viên của hội đồng có 3 cách bầu khác nhau.
Số thành viên của hội đồng là 5.
Như vậy, theo quy tắc nhân thì số cách bầu là: 3 . 3 . 3 . 3 . 3 = 35.
Bài 8.23 trang 58 SBT Toán 10 Tập 2: Tại một cuộc họp của học sinh các lớp 10A, 10B, 10C, 10D và 10E, ban tổ chức đề nghị đại diện của mỗi lớp trình bày một báo cáo. Bạn đại diện của lớp 10A đề nghị được trình bày báo cáo ngay trước đại diện của lớp 10B và được ban tổ chức đồng ý. Số cách xếp chương trình là:
A. 24.
B. 36.
C. 48.
D. 30.
Lời giải:
Đáp án đúng là: A
Kí hiệu thứ tự các bài báo cáo là 1, 2, 3, 4, 5. Có 4 phương án xếp báo cáo của đại diện của lớp 10B ngay sau báo cáo đại diện của 10A là:
– Phương án 1: 10A báo cáo 1, 10B báo cáo 2;
– Phương án 2: 10A báo cáo 2, 10B báo cáo 3;
– Phương án 3: 10A báo cáo 3, 10B báo cáo 4;
– Phương án 4: 10A báo cáo 4, 10B báo cáo 5.
Đối với mỗi phương án, cách xếp thứ tự báo cáo của 10A và 10B là chỉ có 1 cách, ban tổ chức có thể xếp đại diện của các lớp 10C, 10D và 10E theo thứ tự bất kì vào vị trí các báo cáo còn lại.
Do đó, với mỗi phương án thì số cách xếp là: 1.1.3! = 3.2.1 = 6 (cách)
Như vậy, theo quy tắc cộng thì số cách xếp chương trình là: 6 + 6 + 6 + 6 = 24 (cách).
Bài 8.24 trang 58 SBT Toán 10 Tập 2: Người ta muốn thành lập một uỷ ban gồm 6 thành viên, trong đó có ít nhất 3 thành viên nữ từ một nhóm đại biểu gồm 6 nam và 4 nữ. Số các cách thành lập uỷ ban như vậy là
A. 100.
B. 210.
C. 60.
D. 95.
Lời giải:
Đáp án đúng là: D
Do chỉ có 4 đại biểu nữ nên có 2 phương án:
– Phương án 1: uỷ ban gồm 3 nữ và 3 nam;
– Phương án 2: uỷ ban gồm 4 nữ và 2 nam.
+) Đối với phướng án 1:
Số cách chọn ra 3 người từ 4 đại biểu nữ (không khác nhau) là:
(cách).
Số cách chọn ra 3 người từ 6 đại biểu nam (không khác nhau) là:
(cách).
Như vậy, theo quy tắc nhân thì số cách chọn theo phương án 1 là:
4 . 20 = 80 (cách).
+) Đối với phương án 2: chỉ có duy nhất 1 cách chọn ra 4 người từ 4 đại biểu nữ (nghĩa là cả 4 đại biểu nữ sẽ nằm trong uỷ ban cần lập). Ngoài ra, số cách chọn ra 2 người từ 6 đại biểu nam (không khác nhau) là:
(cách).
Do đó, có đúng 15 cách chọn theo phương án 2.
Từ đó, theo quy tắc cộng thì số các cách thành lập uỷ ban là:
80 + 15 = 95 (cách).
Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 8.27 trang 59 SBT Toán 10 Tập 2: Giá trị của biểu thức bằng...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.