Với giải Câu hỏi trang 102 Toán 10 Tập 1 Chân trời sáng tạo trong Bài tập cuối chương 5 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Chân trời sáng tạo trang 102: Bài tập cuối chương 5
a) Nếu hai vectơ →a,→b cùng phương với →c thì →a và →b cùng phương
b) Nếu hai vectơ →a,→b cùng ngược hướng với →c thì →a và →b cùng hướng
Phương pháp giải
Nhận xét về giá và hướng của hai vectơ →a,→b với vectơ →c để rút ra kết luận.
Lời giải
a)
+) Vectơ →a cùng phương với vectơ →c nên giá của vectơ →a song song với giá của vectơ →c
+) Vectơ →b cùng phương với vectơ →c nên giá của vectơ →b song song với giá của vectơ →c
Suy ra giá của vectơ →a và vectơ →b song song với nhau nên →a và →b cùng phương
Vậy khẳng định trên đúng
b)
Giả sử vectơ →c có hướng từ A sang B
+) Vectơ →a ngược hướng với vectơ →c nên giá của vectơ →a song song với giá của vectơ →c và có hướng từ B sang A
+) Vectơ →b ngược hướng với vectơ →c nên giá của vectơ →b song song với giá của vectơ →c và có hướng từ B sang A
Suy ra, hai vectơ →a và →b cùng hướng
Vậy khẳng định trên đúng.
a) Tính độ dài các vectơ →AC,→BD
b) Tìm trong hình ảnh vectơ đối nhau và có độ dài bằng a√102
Phương pháp giải
a) Bước 1: Tính độ dài AC, BD
Bước 2: Tính độ dài vectơ |→AB|=AB
b) Bước 1: Tìm các đoạn thẳng có độ dài là a√102
Bước 2: Từ các đoạn thẳng trên xác định các vecto cùng phương (giá song song hoặc trùng nhau) nhưng ngược hướng.
Lời giải
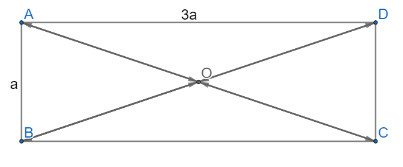
a) Ta có:
AC=BD=√AB2+BC2=√a2+(3a)2=a√10
+) |→AC|=AC=a√10
+) |→BD|=BD=a√10
b) O là giao điểm của hai đường chéo nên ta có:
AO=OC=BO=OD=a√102
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng a√102 là:
→OA và →OC; →AO và →CO; →OB và →OD; →BO và →DO
Phương pháp giải
Quy tắc ba điểm
Quy tắc hình bình hành →AB+→AD=→AC (với ABCD là hình bình hành);
Quy tắc hiệu: →AB−→AC=→CB
Áp dụng các quy tắc trên để xác định vecto →p,→u,→v rồi tính độ dài.→AB=→AO+→OB
Lời giải
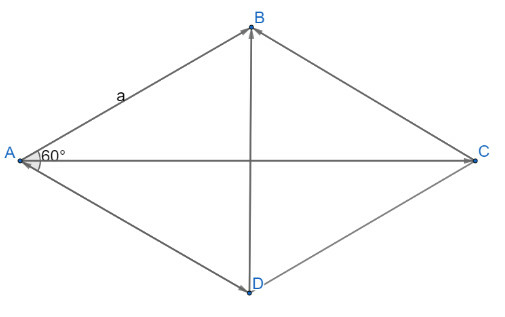
+) ABCD là hình thoi nên cũng là hình bình hành
Áp dụng quy tắc hình bình hành ta có:
→p=→AB+→AD=→AC
+) →u=→AB−→AD=→DB
+) →v=2→AB−→AC=→AB+(→AB−→AC)=→AB+→CB=→AB+→DA=→DB
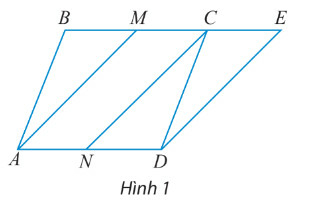
a) Tìm tổng của các vectơ:
→NC và →MC; →AM và →CD; →AD và →NC
b) Tìm các vectơ hiệu:
→NC−→MC; →AC−→BC; →AB−→ME.
c) Chứng minh →AM+→AN=→AB+→AD
Phương pháp giải
a) Chỉ ra các hình bình hành, từ đó suy ra các vectơ bằng nhau và vận dụng quy tắc hình bình hành.
b) Quy tắc hiệu: →AB−→AC=→CB, quy tắc ba điểm →AB=→AO+→OB và thay thế các vectơ bằng nhau →ME=→AD
c) Thay thế các vectơ bằng nhau →AN=→MC; sử dụng quy tắc hình bình hành →AB+→AD=→AC (với ABCD là hình bình hành)
Lời giải
a) Ta có: →CE=→AN⇒CE//AN và CE=AN=ND=BM=MC
Suy ra →MC=→CE
+) →NC+→MC=→NC+→CE=→NE
+) ABCD là hình bình hành nên →CD=→BA
→AM+→CD=→AM+→BA=→BM
+) Ta có →MC=→AN⇒AMCN là hình bình hành nên →NC=→AM
→AD+→NC=→AD+→AM=→AE (vì AMED là hình bình hành)
b) Ta có:
+) →NC−→MC=→NC+→CM=→NM
+) →AC−→BC=→AC+→CB=→AB
+) →AB−→ME=→AB−→AD=→AB+→DA=→DB
c) Ta có:
→AM+→AN=→AM+→MC=→AC
Áp dụng quy tắc hình bình hành vào hình bình hành ABCD ta có
→AB+→AD=→AC
Từ đó suy ra →AM+→AN=→AB+→AD (đpcm)
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 102 Toán 10 Tập 1: Cho 3 vectơ đều khác vectơ . Các khẳng định sau đúng hay sai?
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.