Với giải Câu hỏi trang 13 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 2: Giải bất phương trình bậc hai một ẩn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 13 Bài 2: Giải bất phương trình bậc hai một ẩn
Bài 2 trang 13 Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:
a)
b)
c)
d)
Phương pháp giải
Bước 1: Tìm nghiệm của tam thức (nếu có)
Bước 2: Xác định dấu của a
Bước 3: Xét dấu của tam thức
Lời giải
a) Tam thức bậc hai có hai nghiệm phân biệt là
và có nên khi x thuộc hai nửa khoảng
Vậy tập nghiệm của bất phương trình là
b) Tam thức bậc hai có hai nghiệm phân biệt là
và có nên khi x thuộc khoảng
Vậy tập nghiệm của bất phương trình là
c)
Tam thức bậc hai có và
nên dương với mọi x
Vậy bất phương trình vô nghiệm
d)
Tam thức bậc hai có và
nên với mọi x
Vậy bất phương trình có vô số nghiệm.
Phương pháp giải
Bước 1: Biểu diễn chiểu dài qua chiều rộng (chu vi = 2.(dài + rộng))
Bước 2: Lập công thức tính diện tích (dài*rộng)
Bước 3: Lập bất phương trình và giải
Lời giải
Gọi x là chiều rộng của vườn hoa (, tính bằng đơn vị mét)
Theo giả thiết ta có chiều dài là
Diện tích của vườn hoa có phương trình như sau
Ta có bất phương trình thỏa mãn bài toán như sau:
Xét tam thức có hai nghiệm phân biệt là và nên khi x thuộc đoạn
Vậy khi chiều rộng nằm trong đoạn mét thì diện tích vườn hoa ít nhất là 50 .
a) Bóng có thể cao trên 7 m không?
b) Bóng ở độ cao trên 5 m trong khoảng thời gian bao lâu? Làm tròn kết quả đến hàng phần trăm.
Phương pháp giải
Bước 1: Lập bất phương trình
Bước 2: Tìm nghiệm (nếu có) của tam thức bậc hai
Bước 3: Xét dấu của tam thức bậc hai
Lời giải
a) Theo giả thiết ta có bất phương trình sau:
Xét tam thức có và
nên âm với mọi t, suy ra bât phương trình vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau:
Xét tam thức có hai nghiệm phân biệt là và
nên dương khi t nằm trong khoảng
Vậy khi t nằm trong khoảng giây thì bóng ở độ cao trên 5 m.
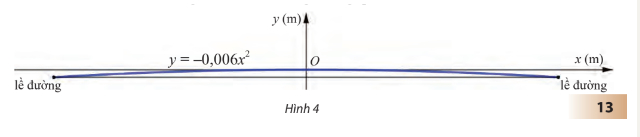
Phương pháp giải
Bước 1: Lập bất phương trình
Bước 2: Tìm nghiệm (nếu có) của tam thức bậc hai
Bước 3: Xét dấu của tam thức bậc hai
Lời giải
15 cm = 0,15 m
Tại vì gốc tọa độ đặt tại tim đường nên độ cao của lề đường so với tim đường là âm
Để tim đường cao hơn đường không quá 15 cm thì ta có bât phương trình sau:
Xét tam thức bậc hai có hai nghiệm phân biệt là và nên dương khi x thuộc hai nửa khoảng
Vậy khi chiều rộng của đường lớn hơn 10 m thì tim đường cao hơn đường không quá 15 cm.
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
HĐ Khởi động trang 11 Toán 10 Tập 2: Với giá trị nào của x thì tam thức bậc hai mang dấu dương?
Thực hành 2 trang 12 Toán 10 Tập 2: Giải các bất phương trình bậc hai sau...
Bài 2 trang 13 Toán 10 Tập 2: Giải các bất phương trình bậc hai sau...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.