Toán 10 Kết nối tri thức trang 42 Bài 6: Hệ thức lượng trong tam giác

Giang Ngày: 12-02-2023 Lớp 10

454

Với giải Câu hỏi trang 42 Toán 10 Tập 1 Kết nối tri thức trong Bài 6: Hệ thức lượng trong tam giác học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Kết nối tri thức trang 42 Bài 6: Hệ thức lượng trong tam giác

Vận dụng 3 trang 42 Toán lớp 10: Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17. Dùng chế dộ tình khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên hòa bình.

Vận dụng 3 trang 41 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

Phương pháp giải:

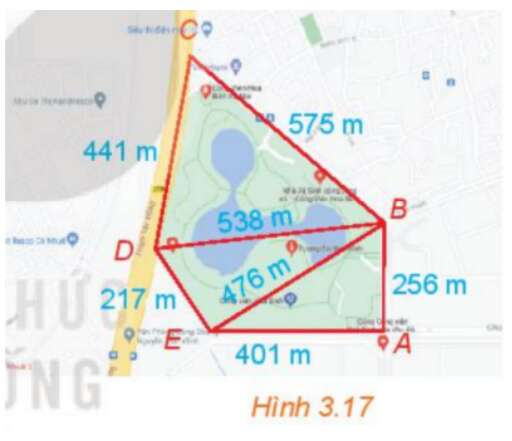
Bước 1: Tính diện tích các tam giác CBD, DBE, EBA bằng công thức Herong:

$S = \sqrt{p (p - a) (p - b) (p - c)}$

Bước 2: Tính diện tích ngũ giác ABCDE, bằng tổng diện tích các tam giác CBD, DBE, EBA.

Lời giải:

Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)

Và nửa chu vi là: $\frac{441 + 575 + 538}{2} = 777 (m)$

Do đó: $S_{C D B} = \sqrt{777. (777 - 441) . (777 - 575) . (777 - 538)} \approx 112267, 7 (m^{2})$

Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)

Và nửa chu vi là: $\frac{217 + 476 + 538}{2} = 615, 5 (m)$

Do đó: $S_{D B E} = \sqrt{615, 5. (615, 5 - 217) . (615, 5 - 476) . (615, 5 - 538)} \approx 51495, 13 (m^{2})$

Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)

Và nửa chu vi là: $\frac{401 + 476 + 256}{2} = 566, 5 (m)$

Do đó: $S_{A B E} = \sqrt{566, 5. (566, 5 - 401) . (566, 5 - 476) . (566, 5 - 256)} \approx 51327, 97 (m^{2})$

Vậy diện tích S của ngũ giác ABCDE là: $S = S_{C D B} + S_{D B E} + S_{A B E} \approx 112267, 7 + 51495, 13 + 51327, 97 = 215090, 8 (m^{2})$

Chú ý: +) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”

+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.

BÀI TẬP

Bài 3.5 trang 42 Toán lớp 10: Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.

Phương pháp giải:

Bước 1: Tính cos A bằng công thức: $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$

Bước 2: Tính S bằng công thức Herong: $S = \sqrt{p (p - a) (p - b) (p - c)}$ với $p = \frac{a + b + c}{2}$

Bước 3: Tính r bằng công thức $S = p r$ .

Lời giải:

Từ định lí cosin ta suy ra $\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{5^{2} + 8^{2} - 6^{2}}{2.5.8} = \frac{53}{80}$

Tam giác ABC có nửa chu vi là: $p = \frac{a + b + c}{2} = \frac{6 + 5 + 8}{2} = 9, 5.$

Theo công thức Herong ta có: $S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{9, 5. (9, 5 - 6) . (9, 5 - 5) . (9, 5 - 8)} \approx 14, 98$

Lại có: $S = p r \Rightarrow r = \frac{S}{p} = \frac{14, 98}{9, 5} = 1, 577.$

Vậy $\cos A = \frac{53}{80}$ ; $S \approx 14, 98$ và $r = 1, 577.$

Bài 3.6 trang 42 Toán lớp 10: Cho tam giác ABC có $a = 10, \hat{A} = 45^{o}, \hat{B} = 70^{o}$ . Tính R,b,c.

Phương pháp giải:

Bước 1: Tính R và b bằng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

Bước 2: Tính $\hat{C}$ và suy ra c bằng định lí sin.

Lời giải:

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

$\Rightarrow R = \frac{a}{2 \sin A}; b = \frac{a . \sin B}{\sin A}$

Mà $a = 10, \hat{A} = 45^{o}, \hat{B} = 70^{o}$

$\Rightarrow R = \frac{10}{2 \sin 45^{o}} = 5 \sqrt{2}; b = \frac{a . \sin 70^{o}}{\sin 45^{o}} \approx 13, 29$

Mặt khác: $\hat{A} = 45^{o}, \hat{B} = 70^{o} \Rightarrow \hat{C} = 65^{o}$

Từ định lí sin ta suy ra: $c = \frac{a . \sin C}{\sin A} = \frac{10. \sin 65^{o}}{\sin 45^{o}} \approx 12, 82.$

Vậy $R = 5 \sqrt{2}; b \approx 13, 29$ ; $c \approx 12, 82.$

Bài 3.7 trang 42 Toán lớp 10: Giải tam giác ABC và tính diện tích của tam giác đó, biết $\hat{A} = 15^{o}, \hat{B} = 130^{o}, c = 6$ .

Phương pháp giải:

Tính a, b, $\hat{C}$ và S

Bước 1: Tính $\hat{C}$ rồi suy ra a, b bằng định lí sin: $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Bước 2: Tính $S = \frac{1}{2} b c . \sin A$ .

Lời giải:

Ta có: $\hat{A} = 15^{o}, \hat{B} = 130^{o} \Rightarrow \hat{C} = 35^{o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

$\Rightarrow b = \frac{c . \sin B}{\sin C}; a = \frac{c . \sin A}{\sin C}$

Mà $\hat{A} = 15^{o}, \hat{B} = 130^{o}, \hat{C} = 35^{o}, c = 6$

$\Rightarrow b = \frac{6. \sin 130^{o}}{\sin 35^{o}} \approx 8; a = \frac{6. \sin 15^{o}}{\sin 35^{o}} \approx 2, 7$

Diện tích tam giác ABC là $S = \frac{1}{2} b c . \sin A = \frac{1}{2} .8 .6 . \sin 15^{o} \approx 6, 212.$

Vậy $a \approx 2, 7; b \approx 8$ ; $\hat{C} = 35^{o}$ ; $S \approx 6, 212.$

Bài 3.8 trang 42 Toán lớp 10: Một tàu đánh cá xuất phát từ cảng A, đi theo hướng $S 70^{o} E$ với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8 km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.

a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Lời giải a

Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu

Phương pháp giải:

Bước 1: Vẽ hình mô tả đường đi từ cảng A, đến nơi mà động cơ hỏng (kí hiệu là B) và hòn đảo (kí hiệu là C) nơi tàu neo đậu.

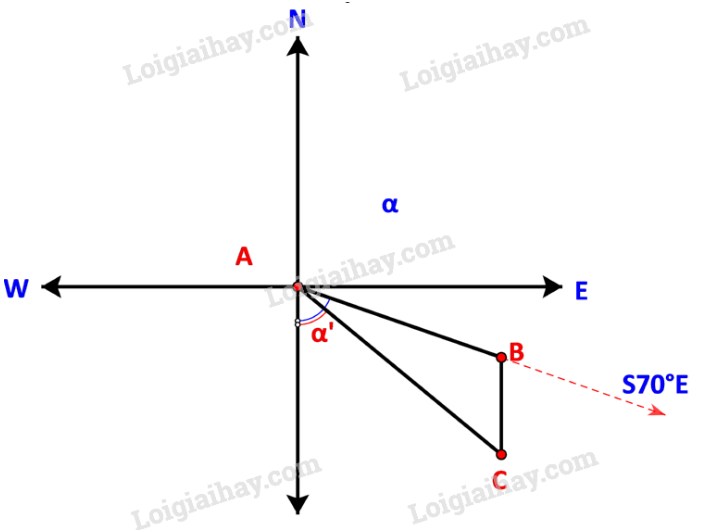
Bài 3.8 trang 42 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 1)

Bước 2: Tính góc $\hat{A B C}$ , quãng đường tàu đi được sau 90 phút () và quãng đường tàu trôi tự do ().

Bước 3: Tính khoảng cách từ cảng tới nơi tàu neo đậu (đoạn AC) bằng cách áp dụng định lí cosin tại đỉnh B.

Lời giải:

Ta có sơ đồ đường đi như sau:

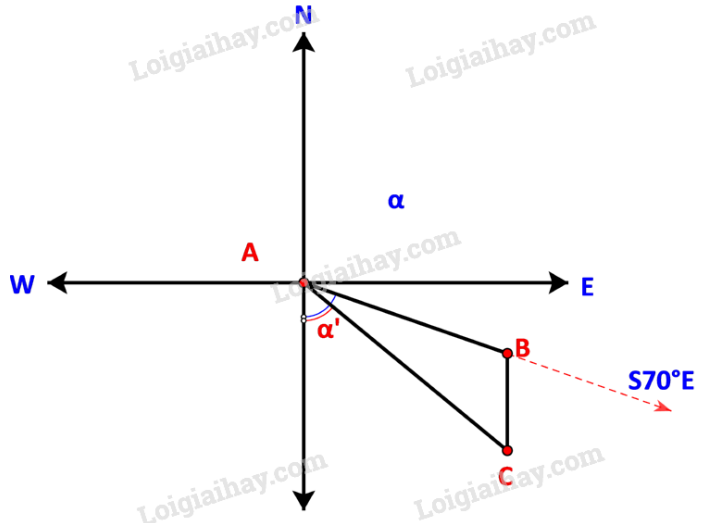
Bài 3.8 trang 42 Toán lớp 10 Tập 1 I Kết nối tri thức với cuộc sống (ảnh 2)

Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.

Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC (hay b).

Ban đầu tàu di chuyển theo hướng $S 70^{o} E$ nên $\hat{B A S} = 70^{o}$ . Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.

$\Rightarrow \hat{A B C} = 180^{o} - \hat{B A S} = 110^{o}$

Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:

70.1,5 = 105 (km) hay c = 105.

Quãng đường tàu trôi tự do là:

8.2 = 16 (km) hay a = 16.

Áp dụng định lí cosin cho tam giác ABC ta có:

$b^{2} = a^{2} + c^{2} - 2 a c . \cos B$

$\begin{array}{l} \Rightarrow b^{2} = 16^{2} + 105^{2} - 2.16.105. \cos 110^{o} \approx 12150, 632 \\ \Rightarrow b \approx 110, 23. \end{array}$

Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 110,23 km.

Lời giải b

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

Phương pháp giải:

Bước 1: Trên sơ đồ: xác định góc nào là hướng từ cảng A tới đảo nơi tàu neo đậu.

Bước 2: Tính sin $\hat{B A C}$ dựa vào định lí sin

Bước 3: Suy ra góc cần tính và kết luận.

Lời giải:

Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là $S α^{o} E$ với $α^{o} = \hat{C A S}$ .

Áp dụng định lí sin cho tam giác ABC ta có:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$ $\Rightarrow \sin A = \frac{a . \sin B}{b}$

Mà $\hat{B} = 110^{o}$ ; $b \approx 110, 23$ ; a = 16.

$\begin{array}{l} \Rightarrow \sin A = \frac{16. \sin 110^{o}}{110, 23} \approx 0, 136 \\ \Rightarrow \hat{A} \approx 7, 84^{o} (d o \hat{A} < 90^{o}) \end{array}$