Toán 10 Kết nối tri thức trang 67 Bài 11: Tích vô hướng của hai vecto

Toán 10 Kết nối tri thức trang 67 Bài 11: Tích vô hướng của hai vecto

Giang Ngày: 12-02-2023 Lớp 10

273

Với giải Câu hỏi trang 67 Toán 10 Tập 1 Kết nối tri thức trong Bài 11: Tích vô hướng của hai vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Kết nối tri thức trang 67 Bài 11: Tích vô hướng của hai vecto

Câu hỏi 1 trang 67 Toán 10: Khi nào thì tích vô hướng của hai vectơ $\vec{u}, \vec{v}$ là một số dương? Là một số âm?

Phương pháp giải:

+) Tích vô hướng của hai vectơ $\vec{u}, \vec{v}$ : $\vec{u} . \vec{v} = | \vec{u} | . | \vec{v} | . \cos (\vec{u}, \vec{v})$

Nhận xét: $\vec{u} . \vec{v}$ cùng dấu với $\cos (\vec{u}, \vec{v})$

Lời giải:

Dễ thấy: $\vec{u} . \vec{v}$ cùng dấu với $\cos (\vec{u}, \vec{v})$ (do $| \vec{u} | . | \vec{v} | > 0$ ). Do đó:

+) $\vec{u} . \vec{v} > 0$ $\Leftrightarrow \cos (\vec{u}, \vec{v}) > 0$ hay $0^{o} \leq (\vec{u}, \vec{v}) < 90^{o}$

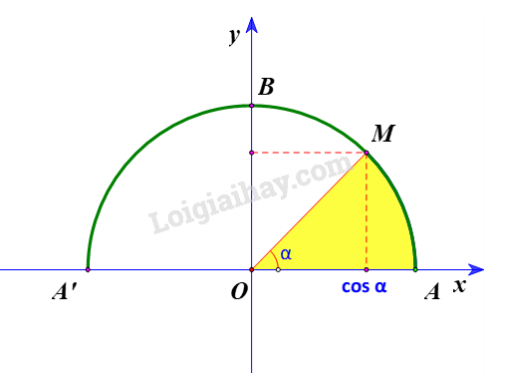
Câu hỏi 1 trang 67 Toán 10 Tập 1 I Kết nối tri thức (ảnh 1)

+) $\vec{u} . \vec{v} < 0$ $\Leftrightarrow \cos (\vec{u}, \vec{v}) < 0$ hay $90^{o} < (\vec{u}, \vec{v}) \leq 180^{o}$

Vậy $\vec{u} . \vec{v} > 0$ nếu $0^{o} \leq (\vec{u}, \vec{v}) < 90^{o}$ và $\vec{u} . \vec{v} < 0$ nếu $90^{o} < (\vec{u}, \vec{v}) \leq 180^{o} .$

2. TÍCH VÔ HƯỚNG CỦA HAI VECTO

Câu hỏi 2 trang 67 Toán 10: Khi nào thì ${(\vec{u} . \vec{v})}^{2} = {(\vec{u})}^{2} . {(\vec{v})}^{2}$ ?

Phương pháp giải:

+) $\vec{u} . \vec{v} = | \vec{u} | . | \vec{v} | . \cos (\vec{u}, \vec{v})$

+) ${\vec{u}}^{2} = {| \vec{u} |}^{2}$ với mọi vectơ $\vec{u}$

Lời giải:

${(\vec{u} . \vec{v})}^{2} = {(\vec{u})}^{2} . {(\vec{v})}^{2}$ $\Leftrightarrow {[| \vec{u} | . | \vec{v} | . \cos (\vec{u}, \vec{v})]}^{2} = {| \vec{u} |}^{2} . {| \vec{v} |}^{2}$

$\begin{array}{l} \Leftrightarrow {[\cos (\vec{u}, \vec{v})]}^{2} = 1 \\ \Leftrightarrow [\begin{array}{l} \cos (\vec{u}, \vec{v}) = 1 \\ \cos (\vec{u}, \vec{v}) = - 1 \end{array} \end{array}$

$\Leftrightarrow [\begin{array}{l} (\vec{u}, \vec{v}) = 0^{o} \\ (\vec{u}, \vec{v}) = 180^{o} \end{array}$

Hay hai vectơ $\vec{u}, \vec{v}$ cùng phương.

Vậy hai vectơ $\vec{u}, \vec{v}$ cùng phương thì ${(\vec{u} . \vec{v})}^{2} = {(\vec{u})}^{2} . {(\vec{v})}^{2}$

Luyện tập 2 trang 67 Toán 10: Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính $\vec{A B} . \vec{A C}$ theo a,b,c.

Phương pháp giải:

+) Tích vô hướng: $\vec{u} . \vec{v} = | \vec{u} | . | \vec{v} | . \cos (\vec{u}, \vec{v})$

Lời giải:

Ta có: $\vec{A B} . \vec{A C} = | \vec{A B} | . | \vec{A C} | . \cos (\vec{A B}, \vec{A C})$

Mà $(\vec{A B}, \vec{A C}) = \hat{B A C}$ $\Rightarrow \cos (\vec{A B}, \vec{A C}) = \cos \hat{B A C}$

Lại có: $\cos \hat{B A C} = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ (suy ra từ định lí cosin)

Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Hoạt động 1 trang 66 Toán 10: Trong hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ AB và AC. Hãy tìm số đo các góc giữa BC và DB , DA và DB...

Câu hỏi trang 66 Toán 10: Khi nào thì góc giữa hai vectơ bằng , bằng ...

Luyện tập 1 trang 66 Toán 10: Cho tam giác đều ABC. Tính ....

Câu hỏi 1 trang 67 Toán 10: Khi nào thì tích vô hướng của hai vectơ là một số dương? Là một số âm?..

Câu hỏi 2 trang 67 Toán 10: Khi nào thì ?...

Luyện tập 2 trang 67 Toán 10: Cho tam giác AB C có BC = a, CA = b, AB = c. Hãy tính theo a,b,c...

Hoạt động 2 trang 68 Toán 10: Cho hai vectơ cùng phương và . Hãy kiểm tra công thức theo từng trường hợp sau:...

Hoạt động 3 trang 68 Toán 10: Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương $\vec{u} = (x; y)$ và $\vec{v} = (x^{'}; y^{'})$ ...

Luyện tập 3 trang 68 Toán 10: Tích vô hướng và góc giữa hai vectơ ...

Hoạt động 4 trang 68 Toán 10: Cho ba vectơ ...

Luyện tập 4 trang 70 Toán 10: Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác....

Vận dụng trang 70 Toán 10: Một lực không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực được phân tích thành hai lực thành phần là và ...

Bài 4.21 trang 70 Toán 10: Trong mặt phẳng tọa độ Oxy, hãy tính góc giữa hai vectơ và trong mỗi trường hợp sau:...

Bài 4.22 trang 70 Toán 10: Tìm điều kiện của để:...

Bài 4.23 trang 70 Toán 10: Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2), B(-4; 3). Gọi M (t; 0) là một điểm thuộc trục hoành....

Bài 4.24 trang 70 Toán 10: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A (-4; 1), B (2;4), C (2; -2)...

Bài 4.25 trang 70 Toán 10: Chứng minh rằng với mọi tam giác ABC, ta có:...

Bài 4.26 trang 70 Toán 10: Cho tam giác ABC có trọng tâm G. Chứng minh rằng với mọi điểm M, ta có:...

Từ khóa :

Giải bài tập Toán 10

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

55

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

47

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

46

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

58

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.