Toptailieu.vn xin giới thiệu 43 câu trắc nghiệm Tích vô hướng của hai vecto Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
43 câu trắc nghiệm Tích vô hướng của hai vecto Kết nối tri thức (có đáp án 2023) CHỌN LỌC
Lý thuyết
1. Định nghĩa
Cho hai vectơ ![]() và
và ![]() đều khác vectơ
đều khác vectơ ![]() . Tích vô hướng của
. Tích vô hướng của ![]() và
và ![]() là một số, kí hiệu là
là một số, kí hiệu là ![]() .
.![]() được xác định bởi công thức sau:
được xác định bởi công thức sau:
![]() .
.![]() = |
= |![]() |.|
|.|![]() |.cos(
|.cos(![]() ,
,![]() )
)
Trường hợp ít nhất một trong hai vectơ ![]() và
và ![]() bằng vectơ
bằng vectơ ![]() ta quy ước:
ta quy ước:
![]() .
.![]() = 0
= 0
Chú ý
+) Với ![]() và
và ![]() khác vectơ
khác vectơ ![]() ta có:
ta có:
![]() .
.![]() = 0 ⇔
= 0 ⇔ ![]() ⊥
⊥ ![]()
+) Khi ![]() =
= ![]() tích vô hướng
tích vô hướng ![]() .
.![]() được kí hiệu là
được kí hiệu là ![]() và số này được gọi là bình phương vô hướng của vectơ
và số này được gọi là bình phương vô hướng của vectơ ![]()
Ta có:
![]() = |
= |![]() |.|
|.|![]() |.cos0o = |
|.cos0o = |![]() |
|
2. Các tính chất của tích vô hướng
Người ta chứng minh được các tính chất sau đây của tích vô hướng:

Nhận xét. Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
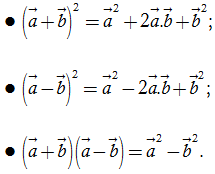
3. Biểu thức tọa độ của tích vô hướng
Trên mặt phẳng tọa độ (O;![]() ;
;![]() ), cho hai vectơ:
), cho hai vectơ:
![]() = (a1,a2),
= (a1,a2), ![]() (b1,b2)
(b1,b2)
Khi đó tích vô hướng ![]() .
.![]()
![]() .
.![]() = a1b1 + a2b2
= a1b1 + a2b2
Nhận xét. Hai vectơ:
![]() = (a1,a2),
= (a1,a2), ![]() (b1,b2)
(b1,b2)
đều khác vectơ ![]() vuông góc với nhau khi và chỉ khi: a1b1 + a2b2 = 0.
vuông góc với nhau khi và chỉ khi: a1b1 + a2b2 = 0.
4. Ứng dụng
a) Độ dài của vectơ
Độ dài của vectơ ![]() = (a1, a2), được tính theo công thức:
= (a1, a2), được tính theo công thức:
![]()
b) Góc giữa hai vectơ
Từ định nghĩa tích vô hướng của hai vectơ ta suy ra nếu ![]() = (a1, a2) và
= (a1, a2) và ![]() = (b1, b2) đều khác
= (b1, b2) đều khác ![]() thì ta có:
thì ta có:
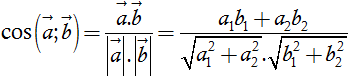
c) Khoảng cách giữa hai điểm
Khoảng cách giữa hai điểm A(xA; yA) và B(xB; yB) được tính theo công thức:
![]()
Bài tập
Câu 1. Trong mp Oxy cho A(4;6), B(1;4), C(7;![]() ). Khảng định nào sau đây sai
). Khảng định nào sau đây sai
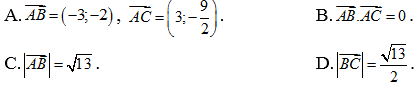
Lời giải
Chọn D
Phương án A: ![]() = (-3;-2), nên loại A.
= (-3;-2), nên loại A.
Phương án B: ![]() .
.![]() = 0 nên loại B.
= 0 nên loại B.
Phương án C : |![]() | =
| = ![]() nên loại C.
nên loại C.![]()
Phương án D: Ta có ![]() suy ra
suy ra 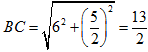 nên chọn D.
nên chọn D.
Câu 2. Cho ![]() và
và ![]() là hai vectơ cùng hướng và đều khác vectơ
là hai vectơ cùng hướng và đều khác vectơ ![]() . Trong các kết quả sau đây, hãy chọn kết quả đúng:
. Trong các kết quả sau đây, hãy chọn kết quả đúng:
![]()
Lời giải
Chọn A
Ta thấy vế trái của 4 phương án giống nhau.
Bài toán cho ![]() và
và ![]() là hai vectơ cùng hướng và đều khác vectơ
là hai vectơ cùng hướng và đều khác vectơ ![]() suy ra (
suy ra (![]() ,
,![]() ) = 0o
) = 0o
Do đó ![]() nên chọn A
nên chọn A
Câu 3. Cho các vectơ ![]() = (1;-2),
= (1;-2), ![]() = (-2;-6). Khi đó góc giữa chúng là
= (-2;-6). Khi đó góc giữa chúng là
A.45o. B. 60o. C. 30o. D. 135o.
Lời giải
Chọn A
Ta có ![]() = (1;-2),
= (1;-2), ![]() = (-2;-6), suy ra
= (-2;-6), suy ra 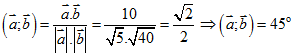 .
.
Câu 4. Cho ![]() = (-2;-1),
= (-2;-1), ![]() = (3;-1). Tính góc của (
= (3;-1). Tính góc của (![]() ,
,![]() )
)
A.135o. B. -![]() . C. -135o. D.
. C. -135o. D. 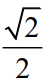 .
.
Lời giải
Chọn A
Ta có 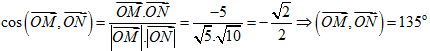 .
.
Câu 5. Trong mặt phẳng Oxy cho ![]() = (1;3),
= (1;3), ![]() = (-2;1). Tích vô hướng của 2 vectơ
= (-2;1). Tích vô hướng của 2 vectơ ![]() .
.![]() là:
là:
A. 1. B. 2. C. 3. D. 4.
Lời giải
Chọn A
Ta có ![]() = (1;3),
= (1;3), ![]() = (-2;1), suy ra
= (-2;1), suy ra ![]() .
.![]() = 1.(-2) + 3.1 = 1.
= 1.(-2) + 3.1 = 1.
Câu 6. Cặp vectơ nào sau đây vuông góc?
A. ![]() = (2;-1) và
= (2;-1) và ![]() = (-3;4). B.
= (-3;4). B. ![]() = (3;-4) và
= (3;-4) và ![]() = (-3;4).
= (-3;4).
C. ![]() = (-2;-3) và
= (-2;-3) và ![]() = (-6;4). D.
= (-6;4). D. ![]() = (7;-3) và
= (7;-3) và ![]() = (3;-7).
= (3;-7).
Lời giải
Chọn C
Phương án A: ![]() .
.![]() = 2.(-3) + (-1).4 = -10 ≠ 0 suy ra A sai.
= 2.(-3) + (-1).4 = -10 ≠ 0 suy ra A sai.
Phương án B: ![]() .
.![]() = 3.(-3) + (-4).4 ≠ 0 suy ra B sai.
= 3.(-3) + (-4).4 ≠ 0 suy ra B sai.
Phương án C: ![]() .
.![]() = -2.(-6) - 3.4 = 0 ⇒
= -2.(-6) - 3.4 = 0 ⇒ ![]() ⊥
⊥![]() suy ra C đúng.
suy ra C đúng.
Phương án D: ![]() .
.![]() = 7.3 + (-3).(-7) = 42 ≠ 0 suy ra D sai.
= 7.3 + (-3).(-7) = 42 ≠ 0 suy ra D sai.
Câu 7. Cho 2 vec tơ ![]() = (a1;a2),
= (a1;a2), ![]() = (b1;b2), tìm biểu thức sai:
= (b1;b2), tìm biểu thức sai:

Lời giải
Chọn C
Phương án A : biểu thức tọa độ tích vô hướng ![]() .
.![]() = a1.b1+ a2.b2 nên loại A
= a1.b1+ a2.b2 nên loại A
Phương án B : Công thức tích vô hướng của hai véc tơ ![]() .
.![]() = |
= |![]() |.|
|.|![]() |.cos(
|.cos(![]() ,
,![]() ) nên loại B
) nên loại B
Phương án C: ![]() nên chọn C.
nên chọn C.
Câu 8. Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai?

Lời giải
Chọn C
Ta đi tính tích vô hướng ở các phương án. So sánh vế trái với vế phải.
Phương án A: ![]() nên loại A.
nên loại A.
Phương án B:![]() nên loại B.
nên loại B.
Phương án C:![]() , nên chọn C.
, nên chọn C.
Câu 9. Cho ABC là tam giác đều. Mệnh đề nào sau đây đúng?

Lời giải
Chọn D
Phương án A: Do![]() nên loại A.
nên loại A.
Phương án B: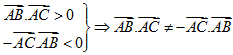 nên loại B.
nên loại B.
Phương án C: Do![]() và
và![]() không cùng phương nên loại C.
không cùng phương nên loại C.
Phương án D:AB = AC = BC = a, ![]() nên chọn D.
nên chọn D.
Câu 10. Cho tam giác ABC có A(1;2), B(-1;1), C(5;-1).Tính cosA
![]()
Lời giải
Chọn B
Ta có ![]() = (-2;-1),
= (-2;-1), ![]() = (4;-3) suy ra
= (4;-3) suy ra
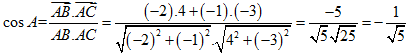 .
.
Câu 11. Cho hình vuông ABCD tâm O. Hỏi mệnh đề nào sau đây sai?

Lời giải
Chọn C
Phương án A:![]() ⊥
⊥![]() suy ra
suy ra ![]() .
.![]() = 0 nên loại A.
= 0 nên loại A.
Phương án B:![]() .
.![]() = 0 và
= 0 và ![]()
![]() .
.![]() = 0 suy ra :
= 0 suy ra :![]() .
.![]() =
= ![]()
![]() .
.![]() = 0 nên loại B.
= 0 nên loại B.
Phương án C: ![]() .
.
![]() nên chọn C.
nên chọn C.
Câu 12. Cho hình vuông ABCD cạnh a . Hỏi mệnh đề nào sau đây sai?

Lời giải
Chọn B
Phương án A:Do![]() nên loạiA.
nên loạiA.
Phương án B:Do![]() nên chọn B.
nên chọn B.
Câu 13. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Câu nào sau đây sai?
![]()
Lời giải
Chọn D
Phương án A:![]() nên loại A.
nên loại A.
Phương án B:![]() ⊥
⊥![]() suy ra
suy ra ![]() .
.![]() = 0 nên loại B.
= 0 nên loại B.
Phương án C:![]() ⊥
⊥![]() suy ra
suy ra ![]() .
.![]() = 0 nên loại C.
= 0 nên loại C.
Phương án D: ![]() không vuông góc với
không vuông góc với ![]() suy ra
suy ra ![]() .
.![]() ≠ 0 nên chọn D .
≠ 0 nên chọn D .
Câu 14. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Khi đó ![]() bằng :
bằng :
A.![]() . B.-
. B.-![]() . C.0. D.9a2.
. C.0. D.9a2.
Lời giải
Chọn B
Ta có ![]() nên chọn B.
nên chọn B.
Câu 15. Cho tam giác đều ABC cạnh a, với các đường cao AH, BK vẽ HI⊥AC. Câu nào sau đây đúng?

Lời giải
Chọn D
Phương án A:![]() nên đẳng thức ở phương án A là đúng.
nên đẳng thức ở phương án A là đúng.
Phương án B:![]() nên đẳng thức ở phương án B là đúng.
nên đẳng thức ở phương án B là đúng.
Phương án C: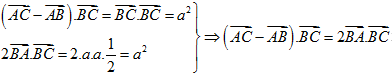 nên đẳng thức ở phương án C là đúng.
nên đẳng thức ở phương án C là đúng.
Vậy chọn D.
Câu 16. Cho tam giác đều ABC cạnh a, với các đường cao AH, BK vẽ HI⊥AC. Câu nào sau đây đúng?
![]()
Lời giải
Chọn C
Phương án A:do ![]() nên loại A
nên loại A
Phương án B:do ![]() nên loại B
nên loại B
Phương án C:do ![]() nên chọn C
nên chọn C
Câu 17. Trong mặt phẳng ![]() cho 2 vectơ :
cho 2 vectơ : ![]() và
và ![]() Kết luận nào sau đây sai?
Kết luận nào sau đây sai?
![]()
Lời giải
Chọn C
![]() = (3;6);
= (3;6); ![]() =(8;-4)
=(8;-4)
Phương án A: ![]() .
.![]() = 24 - 24 = 0 nên loại A
= 24 - 24 = 0 nên loại A
Phương án B: ![]() .
.![]() = 0 suy ra
= 0 suy ra ![]() vuông góc
vuông góc ![]() nên loại B
nên loại B
Phương án C:![]() nên chọn C.
nên chọn C.
Câu 18. Cho các vectơ ![]() = (1;-3),
= (1;-3), ![]() = (2;5). Tính tích vô hướng của
= (2;5). Tính tích vô hướng của ![]() (
(![]() +2
+2![]() )
)
A.16. B.26. C.36. D.-16.
Lời giải
Chọn D
Ta có ![]() .
.![]() = 10,
= 10, ![]() .
.![]() = -13 suy ra
= -13 suy ra ![]() (
(![]() +2
+2![]() ) = -16.
) = -16.
Câu 19. Cho hình vuông ABCD, tính cos(![]() ,
,![]() )
)
A.![]() . B.-
. B.-![]() . C.
. C.![]() . D.-
. D.-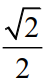 .
.
Lời giải
Chọn D
Đầu tiên ta đi tìm số đo của góc (![]() ,
,![]() ) sau đó mới tính cos(
) sau đó mới tính cos(![]() ,
,![]() )
)
Vì (![]() ,
,![]() ) = 180o - (
) = 180o - (![]() ,
,![]() ) = 135o ⇒ cos(
) = 135o ⇒ cos(![]() ,
,![]() ) = -
) = -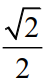 .
.
Câu 20. Cho hai điểm A(-3,2), B(4,3). Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M
A.M(7;0). B.M(5;0). C.M(3;0). D.M(9;0).
Lời giải
Chọn C
Ta có A(-3,2), B(4,3), gọi M(x,0), x>0. Khi đó ![]() = (x+3;-2),
= (x+3;-2), ![]() = (x-4;-3).
= (x-4;-3).
Theo YCBT 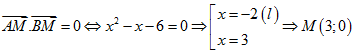 .
.
Câu 21. Cho tam giác ABC vuông cân tại A có BC = a![]() .Tính
.Tính ![]() .
.![]()
![]()
Lời giải
Chọn A
Ta có ![]() .
.
Câu 22. Cho hình vuông ABCD có cạnh a. Tính ![]()
A.0. B.a. C.![]() . D.a2.
. D.a2.
Lời giải
Chọn A
Ta có ![]() = a.a.cos90o = 0.
= a.a.cos90o = 0.
Câu 23. Trong mặt phẳng Oxy, cho ![]() = (2;-1) và
= (2;-1) và ![]() = (-3;4). Khẳng định nào sau đây là sai?
= (-3;4). Khẳng định nào sau đây là sai?
A.Tích vô hướng của hai vectơ đã cho là -10. B.Độ lớn của vectơ ![]() là
là ![]() .
.
C.Độ lớn của vectơ ![]() là 5. D.Góc giữa hai vectơ là 90o.
là 5. D.Góc giữa hai vectơ là 90o.
Lời giải
Chọn D
Ta có ![]() nên B đúng.
nên B đúng.
![]() nên C đúng.
nên C đúng.
![]() .
.![]() = 2.(-3) + (-1).4 = -10 ≠ 0 nên A đúng, D sai.
= 2.(-3) + (-1).4 = -10 ≠ 0 nên A đúng, D sai.
Câu 24. Cho M là trung điểm AB, tìm biểu thức sai:
![]()
Lời giải
Chọn D
Phương án A:![]() ngược hướng suy ra
ngược hướng suy ra ![]() = MA.AB.cos180o = -MA.MB nên loại A.
= MA.AB.cos180o = -MA.MB nên loại A.
Phương án B:![]() ngược hướng suy ra
ngược hướng suy ra ![]() = MA.MB.cos180o = - MA.MB nên loại B.
= MA.MB.cos180o = - MA.MB nên loại B.
Phương án C: ![]() cùng hướng suy ra
cùng hướng suy ra ![]() = AM.AB.cos0o = AM.AB nên loại C.
= AM.AB.cos0o = AM.AB nên loại C.
Phương án D:![]() ngược hướng suy ra
ngược hướng suy ra ![]() = MA.MB.cos180o = -MA.MB nên chọn D.
= MA.MB.cos180o = -MA.MB nên chọn D.
Câu 25. Cho tam giác đều ABC cạnh bằng a và H là trung điểm BC. Tính ![]()
![]()
Lời giải
Chọn B
Ta có ![]() .
.
Câu 26. Biết ![]() ,
, ![]() ≠
≠ ![]() và
và ![]() .
.![]() = -|
= -|![]() |.|
|.|![]() |. Câu nào sau đây đúng
|. Câu nào sau đây đúng
A.![]() và
và ![]() cùng hướng.
cùng hướng.
B.![]() và
và ![]() nằm trên hai dường thẳng hợp với nhau một góc 120o.
nằm trên hai dường thẳng hợp với nhau một góc 120o.
C.![]() và
và ![]() ngược hướng.
ngược hướng.
D. A, B, C đều sai.
Lời giải
Chọn C
Ta có ![]() nên
nên ![]() và
và ![]() ngược hướng
ngược hướng
Câu 27. Tính (![]() ,
,![]() ) biết
) biết ![]() .
.![]() = -
= -![]() |
|![]() |.|
|.|![]() |, (
|, (![]() ,
,![]() ≠
≠ ![]() )
)
A.120o. B.135o. C.150o. D.60o.
Lời giải
Chọn A
![]()
Câu 28. Cho tứ giác lồi ABCD có AD = 6 cm. Đặt ![]() .Tính
.Tính ![]()
A.18 cm2. B.24 cm2. C.36 cm2. D.48 cm2.
Lời giải
Chọn C
![]() suy ra
suy ra ![]() = AD2 = 36 cm2.
= AD2 = 36 cm2.
Câu 29. Cho 2 vectơ ![]() và
và ![]() có |
có |![]() | = 4, |
| = 4, |![]() | = 5 và (
| = 5 và (![]() ,
,![]() ) =120o.Tính |
) =120o.Tính |![]() +
+![]() |
|
A.![]() . B.
. B.![]() . C.21. D.61.
. C.21. D.61.
Lời giải
Chọn A
Ta có ![]() .
.
Câu 30. Cho tam giác ABC có cạnh BC = 6 cm và đường cao AH, H ở trên cạnh BC sao cho BH = 2HC.Tính ![]()
A.-24 cm2. B.24 cm2. C.18 cm2. D.-18 cm2.
Lời giải
Chọn A
Ta có ![]() .
.
Câu 31. Cho tam giác ABC có A(1;2), B(-1;1), C(5;-1).Tính ![]()
A.7. B.5. C.-7. D.-5.
Lời giải
Chọn D
Ta có ![]() = (-2).4 + (-1).(-3) = -5.
= (-2).4 + (-1).(-3) = -5.
Câu 32. Trong mặt phẳng Oxy cho A(-1;1), B(1;3), C(1;-1). Khảng định nào sau đây đúng.
A.![]() = (4;2),
= (4;2), ![]() = (2;-4). B.
= (2;-4). B.![]() ⊥
⊥![]() .
.
C. Tam giác ABC vuông cân tại A. D. Tam giác ABC vuông cân tại B.
Lời giải
Chọn C
Phương án A: do ![]() = (2;2) nên loại A.
= (2;2) nên loại A.
Phương án B: ![]() = (2;2),
= (2;2), ![]() = (0;-4),
= (0;-4),![]() .
.![]() = -8 suy ra
= -8 suy ra![]() không vuông góc
không vuông góc![]() nên loại B.
nên loại B.
Phương án C : Ta có ![]() = (2;2),
= (2;2), ![]() = (2;-2),
= (2;-2), ![]() = (0;-4), suy ra AB = AC =
= (0;-4), suy ra AB = AC = ![]() ,
, ![]() .
.![]() = 0.Nên Tam giác ABC vuông cân tại A.Do đó chọn C.
= 0.Nên Tam giác ABC vuông cân tại A.Do đó chọn C.
Câu 33. Cho ![]() = (1;-2),
= (1;-2), ![]() = (-1;-3). Tính (
= (-1;-3). Tính (![]() ,
,![]() ).
).
A.(![]() ,
,![]() ) = 120o. B.(
) = 120o. B.(![]() ,
,![]() ) = 135o. C.(
) = 135o. C.(![]() ,
,![]() ) = 45o. D.(
) = 45o. D.(![]() ,
,![]() ) = 90o.
) = 90o.
Lời giải
Chọn C
Ta có 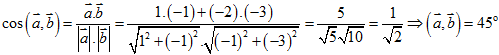 .
.
Câu 34. Cho tam giác ABC vuông tại A có B = 60o,AB = a. Tính ![]()
A.3a2. B.-3a2. C.3a. D. 0.
Lời giải
Chọn B
Ta có 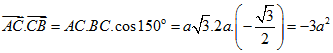 .
.
Câu 35. Cho tam giác ABC vuông tại A có AC = 12 cm. M là trung điểm AC. Tính![]()
A.144 cm2. B.-144 cm2. C.72 cm2. D.-72 cm2.
Lời giải
Chọn D
![]()
Câu 36. Cho tam giác ABC có đường cao BH (H ở trên cạnh AC).Câu nào sau đây đúng
![]()
Lời giải
Chọn C
Ta có ![]() nên chọn C.
nên chọn C.
Câu 37. Cho 2 vectơ đơn vị ![]() và
và ![]() thỏa |
thỏa |![]() +
+![]() | = 2. Hãy xác định (3
| = 2. Hãy xác định (3![]() -4
-4![]() ) (2
) (2![]() +5
+5![]() )
)
A.7. B.5. C.-7. D.-5.
Lời giải
Chọn C
![]()
Câu 38. Cho tam giác ABC. Lấy điểm M trên BC sao cho ![]() .Câu nào sau đây đúng
.Câu nào sau đây đúng
A.M là trung điểm của BC. B.AM là đường phân giác của góc A.
C.AM⊥BC. D. A, B, C đều sai.
Lời giải
Chọn C
Ta có ![]() nên AM⊥BC.
nên AM⊥BC.
Câu 39. Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a.Tính ![]()
A.-9a2. B. 15a2. C. 0. D. 9a2
Lời giải
Chọn A
Vì ![]() nên chọn A.
nên chọn A.
Câu 40. Cho tam giác ABC vuông tại C có AC = 9, BC = 5. Tính ![]()
A.9. B.81. C.3. D.5.
Lời giải
ChọnB
Ta có 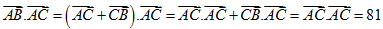 nên chọn B.
nên chọn B.
Câu 41. Cho hai vectơ ![]() và
và ![]() . Biết |
. Biết |![]() | =2 ,
| =2 , ![]() =
= ![]() và (
và (![]() ,
,![]() ) = 120o.Tính |
) = 120o.Tính |![]() +
+![]() |
|
![]()
Lời giải
Chọn C
Ta có ![]() .
.
Câu 42. Cho hai điểm B, C phân biệt. Tập hợp những điểm M thỏa mãn ![]() là :
là :
A.Đường tròn đường kính BC. B. Đường tròn (B;BC).
C. Đường tròn (C;CB). D. Một đường khác.
Lời giải
Chọn A
![]() .
.
Tập hợp điểm M là đường tròn đường kính BC.
Câu 43. Cho ba điểm A, B, C phân biệt. Tập hợp những điểm M mà ![]() là :
là :
A. Đường tròn đường kính AB.
B.Đường thẳng đi qua A và vuông góc với BC.
C. Đường thẳng đi qua B và vuông góc với AC.
D. Đường thẳng đi qua C và vuông góc với AB.
Lời giải
Chọn B
![]() .
.
Tập hợp điểm M là đường thẳng đi qua A và vuông góc với BC.
Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 10: Vecto trong mặt phẳng tọa độ
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.